Глава третья. Динамическое программирование как метод оптимизации. Процессы принятия решении

3.1. Идея и области применения метода. Принцип оптимальности

В общем виде динамическое программирование можно определить как метод оптимизации многошаговых процессов принятия решений, позволяющий указать пути решения целого класса экстремальных задач в теории управления, исследовании операций, экономике. В частности, метод оказывается весьма эффективным при анализе задач с сепарабельной целевой функцией

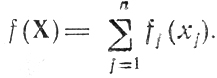
Необходимость принять решение возникает тогда, когда производятся те или иные целенаправленные действия, например некоторая физическая система переводится из одного состояния в другое посредством приложения управляющих воздействий или намечается последовательность формальных преобразований при поиске экстремума функции. Если в рамках любой реальной задачи подобные ситуации возникают периодически, то образуется процесс принятия решений, который может быть назван процессом управления, планирования, поиска экстремума и т. п. в зависимости от того, какая реальность стоит за рассматриваемой задачей. Вообще говоря, ход процессов такого рода заранее не определен, его нужно организовать, причем всегда желательна та организация, которая дает наибольший эффект с точки зрения принятого критерия (z) эффективности действий. Формально это может означать требование минимизации (максимизации) величины указанного критерия (если, конечно, он выражается числом).

Предположим, что интересующий нас процесс принятия решений можно разбить на N шагов. Пусть действия, совершаемые на r-м шаге характеризуются

совокупностью показателей (u_r1, u_r2, ..., u_rM) = U_r, а состояние процесса к началу этого шага - совокупностью параметров (y_r1, y_r2, ...., y_rR) = Y_r. Обычно действия U_r не являются полностью произвольными, а зависят от состояния Y_r, которое возникло перед r-м шагом, т. е. U_r = U_r(Y_r). Нетрудно представить, что результирующее значение критерия r, полученное по окончании процесса, будет определяться теми U_r (r = 1, N), которые были приняты ранее, т. е. z = z(U₁, U₂, ..., U_N). Возникает вопрос: как выбрать Ub U2, ..Uiv, чтобы величина г приняла экстремальное значение? Ответ на него можно в принципе получить, рассматривая г как функцию переменных u_rp (r = 1, N; р = 1, М) и находя экстремум г одним из известных способов, однако этот путь не всегда приводит к цели (особенно, если велико число переменных). Появляется идея провести оптимизацию поэтапно, анализируя последовательно каждый шаг процесса в поисках наилучших вариантов его продолжения, чем и определяется содержание метода динамического программирования, реализующего принцип последовательной оптимизации. Таким образом, важным условием применимости рассматриваемого метода является возможность разбиения процесса принятия решений на ряд однотипных шагов или этапов, каждый из которых планируется отдельно, но с учетом результатов, полученных на других шагах.

В основе динамического программирования лежат два важных принципа. Первый, называемый принципом оптимальности, формулируется следующим образом: необходимо всегда обеспечить оптимальное (в смысле принятого критерия) продолжение процесса относительно уже достигнутого его состояния (Р. Беллман). Другими словами, решение на каждом последующем шаге должно приниматься с учетом результата, полученного на предыдущих шагах. Ниже будет показано, что этот принцип имеет довольно простую математическую интерпретацию, выражающуюся в составлении определенных рекуррентных соотношений.

Второй основной принцип утверждает, что природа задачи, допускающей использование метода динамического программирования, не меняется при изменении количества шагов, т. е. форма такой задачи инвариантна относительно N. В этом смысле всякий конкретный процесс с заданным числом N оказывается как бы вложенным в семейство подобных ему процессов и может рассматриваться с более широких позиций (принцип вложения).

Реализация названных принципов дает гарантию того, что, во-первых, решение, принимаемое на очередном шаге, окажется наилучшим с точки зрения всего процесса в целом (а не "узких интересов" данного этапа) и, во-вторых, последовательность решений одношаговой, двухшаговой и т. д. задач приведет к решению исходной N-шаговой задачи.

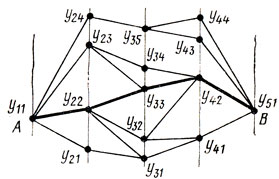
Рис. 3.1

Полезно обратить внимание на специфические особенности построения схем динамического программирования. Обычно они строятся так, что первым исследуется конечный этап того

реального явления, которое отражено в задаче оптимизации. Действительно, этот

этап может быть изучен и спланирован сам по себе наилучшим (в смысле критерия г) образом, поскольку он завершает процесс. Но сделать это можно лишь на основе предположений об'ожидаемых исходах предшествующего (но еще не исследованного) этапа, т. е. о значениях Y что даст набор условно оптимальных решений U_Nopt/Y_N.

Завершив указанные действия, нужно рассмотреть аналогичную задачу применительно к предпоследнему этапу процесса, но потребовать при этом, чтобы желаемый эффект, выраженный в экстремальных значениях z, был достигнут не на этом этапе отдельно, а на двух последних этапах вместе. Тем самым будет найден второй набор условно оптимальных решений (U_N-1, U_N)_opt/Y_N-1 учитывающих результаты U_Nopt. Повторив подобные операции для третьего, четвертого (от конца) и последующих этапов изучаемого процесса, можно в конце концов найти решение задачи в целом, указывающее значения (U₁, U₂,...., U_N)_opt/Y₁, а также z^*. Дополнительные пояснения дает приводимый пример.

Пример: некоторый материальный объект должен перейти из пункта A в пункт В; возможные пути перехода и расстояния указаны на рис 3.1; требуется найти наикратчайший путь (подобным образом могут быть интерпретированы задачи о выборе кратчайшего транспортного маршрута при известной сети дорог, об отыскании критического Пути на сетевом графике и т. д.). Принятие очередного решения означает в данном случае выбор направления выхода из того узлового пункта, куда попал объект; шагом (этапом) процесса является перемещение объекта из одного узла сети (рис 3.1) в другой по допустимому маршруту; состояние процесса непосредственно перед началом очередного этапа характеризуется местоположением объекта y_rs; критерием эффективности действий является пройденное расстояние, величина которого подлежит минимизации (оно определяется масштабом рисунка).

Решение: анализируем последний (четвертый) этап рассматриваемого процесса; здесь по существу нет никакого выбора и приходится констатировать следующее: если результатом действий объекта на третьем этапе явился его выход в точку yiu то кратчайший (и единственный) путь в В есть

точно так же

- первый набор условно оптимальных решений; возможные положения объекта к началу предпоследнего (третьего) этапа есть y_3s (s = 1,....,5); для состояния y₃₁ существует единственное решение - двигаться по линии y₃₁y₄₁y₅₁(U₃, U₄)_opt/y₃₁ для y₃₂ лучшим является продолжение y₃₂y₄₁y₅₁ ≡ (U₃, U₄)_opt/y₃₂ и далее y₃₃y₄₂y₅₁ ≡ (U₃, U₄)_opt/y₃₃, ....., y₃₅y₄₃y₅₁ ≡ (U₃, U₄)_opt/y₃₅ (полезно еще раз заметить, что действия здесь спланированы с учетом требования достичь наибольшего эффекта на двух последних шагах вместе).

Повторяя аналогичные рассуждения применительно к состояниям y_2s (s = 1,...,4), получаем такие результаты: кратчайший путь из y₂₁ в есть y₂₁y₃₁y₄₁y₅₁ из y₂₂-y₂₂y₃₃y₄₂y₅₁, из y₂₃-y₂₃y₃₄y₄₂y₅₁, наконец, из y₂₄-y₂₄y₃₅y₄₃y₅₁.

Теперь остается исследовать точку A; поскольку оптимальные решения для точек y_2s (s = 1,...,4) найдены, достаточно сравнить величины

наименьшей среди них оказывается

Таким образом, методом динамического программирования найден оптимальный с точки зрения минимума длины пути вариант перехода из А в В. Полученное решение оптимально только в указанном смысле; изменение критерия повлечет за собой изменение результата. Например, приписав каждому возможному маршруту некоторую вероятность достижения точки В и потребовав так организовать переход, чтобы эта вероятность была максимальной, можно получить совсем иной результат (в частности, наилучшим может оказаться какой-то периферийный маршрут).

Чтобы завершить общую характеристику метода динамического программирования, обратимся к краткому анализу его преимуществ и недостатков. В первую очередь отметим следующие положительные стороны метода:

- он дает возможность решать задачи, которые раньше не могли быть решены из-за отсутствия соответствующего математического аппарата (например, вариационные задачи с ограничениями-неравенствами или конечномерные экстремальные задачи с дискретной структурой);

- позволяет упростить поиск оптимальных решений в ряде случаев за счет резкого сокращения объемов вычислений (в первую очередь это относится к комбинаторным задачам);

- являясь в своей основе вычислительным, допускает широкое применение средств механизации счета (в первую очередь ЭВМ), что облегчает сложные исследования.

Недостатки:

- отсутствие универсального алгоритма, который был бы пригоден для решения всех задач (алгоритмы, используемые в рамках динамического программирования, объединены лишь общей идеей и в каждом конкретном случае должны формироваться применительно к условиям задачи);

- большие трудности при решении многомерных задач (несмотря на высокую вычислительную эффективность метода, в ряде случаев оказываются недостаточными мощности современных ЭВМ).

Обратимся теперь к выводу формальных соотношений, характеризующих метод динамического программирования (их называют функциональными уравнениями). Поскольку основное внимание здесь уделяется задачам математического программирования, в дальнейшем рассматривается конкретный класс нелинейных конечномерных задач.