3.6. Составление и анализ функциональных уравнений

Для простоты будем рассматривать задачу минимизации функционала вида

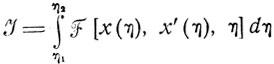
или (в других обозначениях)

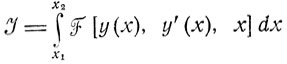
с граничными условиями

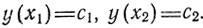
Таким образом, отыскивается кривая y = y^*(x), соединяющая точки (х₁, c₁) и (х₂, c₂), на которой J достигает минимума (рис. 3.5).

Переходя к составлению основного функционального уравнения, разделим интервал [х₁, х₂] на две части [х₁, х̄], [х̄, х₂] и введем в рассмотрение функцию

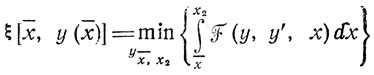
(рассматривается минимум по у на интервале [x̄₁, x₂]). Ясно, что изменения х̄ вызовут соответствующие изменения g (в частности, ξ = 0 при х̄ = х₂ и ξ = J^* при х̄ = х₁). Теперь, в соответствии с принципом оптимальности, можно утверждать

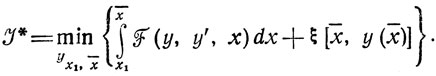(3.5)

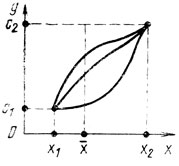
Рис. 3.5

Предположим, что x̄ мало отличается от x₁, т. е. Δ = х̄ - х₁ есть малая положительная величина, которую всегда можно выбрать так, что справедливы приближенные равенства

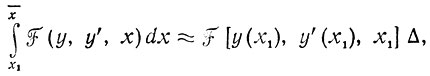
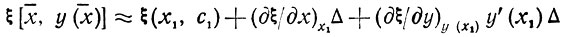
(сумма линейных членов разложения ξ в ряд Тейлора в окрестности точки (х₁, c₁). В этих условиях соотношение (3.5) принимает вид

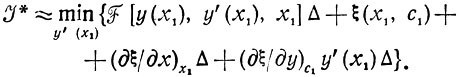(3.6)

Поскольку ξ(x₁,c₁) есть просто J^* (см. определение ξ), равенство (3.6) можно представить как

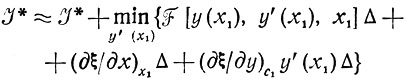
или

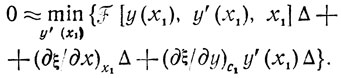<(3.7)br>

Здесь необходимо заметить следующее: приблизив х̄ к x₁ настолько, что стала допустимой линеаризация задачи, следует заменить требование найти оптимальную в смысле min J траекторию y_{x̄, x1} требованием найти оптимальное значение производной y' в точке х₁ (это и сделано выше). Переходя теперь к пределу при Δ→0 в (3.7), имеем

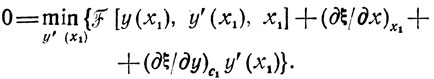(3.8)

Чтобы определить величину y'(х₁) = ŷ', доставляющую минимум вида (3.8), нужно рассмотреть уравнение dF/dy'+(dξ/dy)_c1=0, получаемое дифференцированием суммы в (3.8) и приравниванием производной нулю. В то же время подстановка ŷ' в (3.8) должна обратить эту сумму в нуль (в этом случае она принимает свое наименьшее значение, равное нулю). Следовательно, ŷ' удовлетворяет системе о уравнений

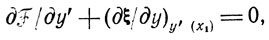(3.9)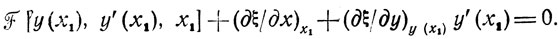

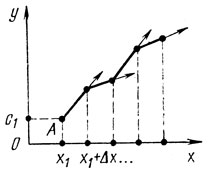
Рис. 3.6

Ее решение должно указать ŷ' (х₁) и тем самым определить направление "выхода" оптимальной кривой y = у^*(х) из точки (x₁, c₁) (рис. 3.6). Зная это, легко выбрать следующую точку с координатами (x₁+Δх; y₁+ŷ;Δx) и повторить для нее всю процедуру отыскания оптимального направления ŷ'(х₁+Δх). Последовательное вычисление оптимальных производных при значениях х = x + lΔх (l = 1, 2, ...) является характерной особенностью рассматриваемого подхода к решению вариационных задач.

Уравнения (3.9) являются, вообще говоря, нелинейными дифференциальными уравнениями в частных производных и могут быть сведены к известным из классического вариационного исчисления уравнениям Эйлера. Для этого достаточно найти полную производную по л: верхней строки (3.9) и частную производную по у нижней строки (3.9), т. е.

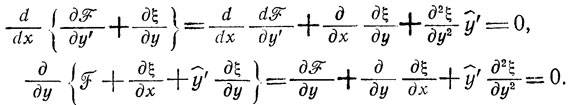(3.11)

Если теперь вычесть (3.11) из (3.10), то новое равенство

окажется просто уравнением Эйлера. Таким образом удается не только установить связь между уравнениями (3.9) и (3.12), но и показать возможности формализации вариационных задач, отличной от классической и базирующейся на принципах динамического программирования.