3.5. Динамическое программирование и вариационные задачи. Дискретная форма условий

Динамическое программирование обнаруживает связь с рядом классических методов, в частности с вариационным исчислением. В вариационных задачах отыскивается экстремальное значение некоторой величины, выражающейся через интеграл, что позволяет надеяться на успешное применение здесь рассматриваемого метода.

Обычно требуется найти экстремум функционала 3

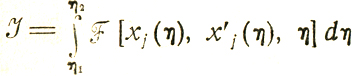
при ограничениях типа уравнений связи

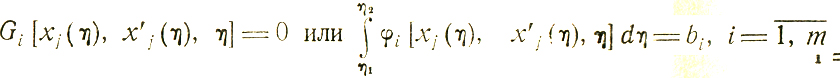
и т. д. Иногда дополнительные условия налагаются на η₁, η₂ и соответствующие им значения x_j(η₁), x_j(η₂), x'_j(η₁), x'_j(η₂).

Классическим примером вариационной задачи является так называемая задача о брахистохроне в следующей формулировке: дана материальная точка с массой га, занимающая в пространстве определенное положение (его удобно принять за начало координат); в момент t = 0 эта точка начинает двигаться под действием силы тяжести Р, чтобы достичь некоторого заданного конечного положения К; требуется найти такую траекторию движения, которая обеспечила бы минимальное время перехода из нуля в К (рис. 3.4). В силу закона сохранения энергии работа, произведенная силой Р на расстоянии х₁ (t), пройденном точкой вдоль направления действия Р к моменту t>0, равна кинетической энергии mv²(t)/2, где v (t) - полная скорость точки в тот же момент; таким образом, v²(t) = 2Px₁(t)/m или v = √2gx₁ (g - ускорение силы тяжести).

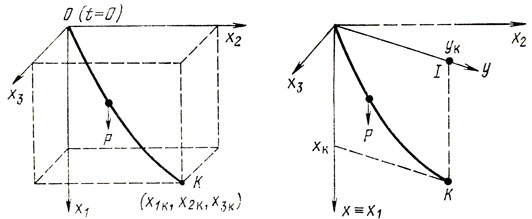
Рис. 3.4

Рассматривая элемент ds дуги ОК, можно утверждать: vdt = ds или dt = ds/v, откуда следует

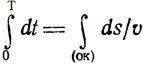
или

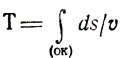
(здесь Т - время перемещения точки из О в К). Используя соотношения

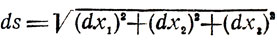
и

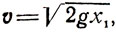
получаем окончательно

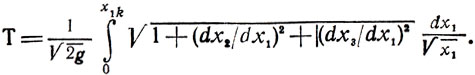
Минимизация Т, как указывалось, составляет основу нашей задачи.

Классический метод решения вариационных задач предусматривает анализ системы дифференциальных уравнений (уравнения Эйлера), позволяющих найти х^*_j (j = 1, ...,n) и J^*. Такой подход предъявляет определенные требования к x_j(η) и подынтегральной функции F[x_j(η), x'_j(η), η] в выражении У (в частности,

необходимо существование производных x_j и F). Нарушение подобных требований приводит к затруднениям, которые либо совершенно исключают возможность использования классического вариационного исчисления, .либо делают эту возможность сомнительной из-за больших затрат усилий и времени на поиск x^*_j(η) (j = 1,...,n). Эти затруднения возникают, например, тогда, когда в задаче есть ограничения-неравенства, функции x_j(η)m среди которых отыскиваются ^**j(r]), заведомо негладкие и т. д. В этих случаях метод динамического программирования оказывается не только применимым, но и часто дает более простую схему решения. Чтобы конкретизировать эти замечания, обратимся к уже знакомой задаче о брахистохроне и рассмотрим последовательность шагов, приводящих к отысканию оптимальной в смысле min Т траектории движения точки из нуля в К.

Прежде всего полезно заметить, что брахистохрона является кривой, лежащей целиком в плоскости I, проходящей через ось х₁ и точку К (рис. 3.4), поэтому s дальнейшем достаточно рассматривать систему координат х, y; здесь

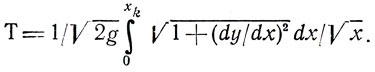
(3.4)

Первое, на что следует обратить внимание при анализе выражения (3.4), - это возможность дискретизации задачи, позволяющая построить процедуру поиска решения, сходную с той, которая была рассмотрена в п. 3.3. Пусть интервал изменения х разбит на N равных частей так, что x_k = NΔx. Координата каждой точки деления с номером r (1≤r≤N-1) есть х_r = r×Δх; соответствующие величины y=y_r позволяют оценить производные функции y = y(х) в точках x_r: y'_r ≈ (y_r+1-y_r)/Δх, r = 1,....., N - 1.

Учитывая это, можно преобразовать интеграл (3.4) следующим образом:

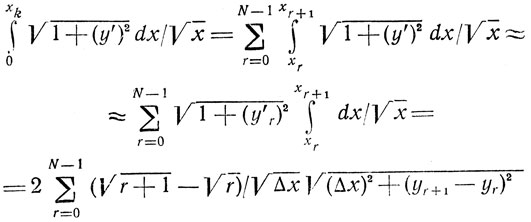
(в основе приближенного равенства здесь лежит предположение о постоянстве величины √(1+(y'_r)²) на интервале [х_r, х_r+1]).

Очевидно, исходная задача свелась к задаче с сепарабельной целевой функцией (относительно переменных Δy_r = y_r+1-y_r), что делает возможным применение метода динамического программирования.

Обозначив, как и ранее, величину

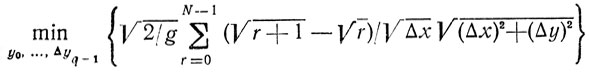
через Ψ_q, приходим к функциональному уравнению

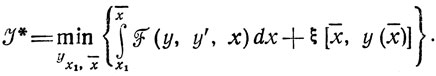
определяющему алгоритм поиска экстремума Т. Преимущество такого подхода в том, что он, во-первых, применим в случаях, когда классические методы неприменимы (разрывность функций, ограничения-неравенства и т. п.), и, во-вторых, позволяет избежать решения систем дифференциальных уравнений далеко не всегда простых.

Вместе с тем сама идея аппроксимации интеграла суммой может не оправдать себя, если требуется высокая точность результата, поэтому имеет смысл остановиться еще на одном варианте использования динамического программирования в вариационном исчислении.