4.1. Основные понятия. Роль численных методов в прикладных исследованиях

Разнообразие нелинейных задач математического программирования (с полной или неполной информацией) вызывает необходимость разработки методов оптимизации, не связанных непосредственно с анализом условий существования X^* и целиком базирующихся на вычислительных и логических операциях. Идеи этих методов обычно просты; как правило, они следуют из эвристических соображений, сводя проблему решения задачи к построению надлежащего алгоритма поиска X^*, z^*, причем желаемые свойства таких алгоритмов оговариваются заранее. Их достижение должно обеспечиваться анализом конечности алгоритма, оценками скорости его сходимости, рациональной организацией вычислений и т. д. Общим здесь является утверждение целесообразности (достаточности) предлагаемых схем решения конкретной экстремальной задачи (необходимость их чаще всего недоказуема).

Центральным вопросом формирования алгоритма поиска оптимума является вопрос сходимости. Каждый алгоритм предлагает правило, в соответствии с которым определяется очередная точка Х_k, подлежащая исследованию с целью подготовки перехода в X_k+1. Процесс поиска X^* характеризуется последовательностью переходов (шагов), причем каждый из них дает некоторую информацию о направлении "движения", величине очередного шага и т. п.

Можно утверждать, что алгоритм сходится, если он либо непосредственно вычисляет экстремальную точку X^* (и соответствующее z^*), либо указывает X^* в виде предельной точки Х_∞ последовательности {Х_k}, k = 1, 2, ... Необходимо подчеркнуть, что лишь в частных случаях удается достичь X^* за конечное число шагов (задачи линейного, квадратичного программирования); в общем случае сходимость имеет место только в предельном смысле.

Отношение, связывающее X_k+1 с Х_k и составляющее основу вычислительной схемы того или иного алгоритма, может принимать разные формы. Простейший его вид - функциональная зависимость X_k+1 = W(X_k) или точечно-точечное отображение, в котором каждая точка X имеет единственный образ W(Х). Более общим является точечно-множественное отображение, где образ W(Х) произвольной точки Х∈U представляет собой некоторое подмножество, включенное в U (символ U обозначает, как и ранее, множество X, допустимых по условиям экстремальной задачи, т. е. ее область определения, см. гл. 1); очевидно, здесь X_k+1∈W(Х_k). Следует также иметь в виду, что характер отображения W может меняться с изменением k (это учитывается в обозначении W_k).

Примерами, иллюстрирующими сделанные замечания, являются:

а) отображение вида

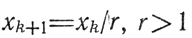
(случай скалярного аргумента Х≡x); здесь возникает последовательность значений х, сходящаяся в пределе (при k→∞) к x_∞ = 0;

б) отображение вида

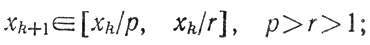
здесь нельзя указать заранее, какая конкретно последовательность точек х будет порождена, так как известно лишь, что

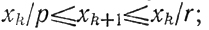
вместе с тем можно утверждать, что она будет сходиться столь же быстро, как и последовательность x_k+1 =x_k/r.

Анализ условий сходимости алгоритмов основывается на следующих понятиях и определениях:

- функция W (X_k) называется напрерывной в точке Х_∞, если из равенства

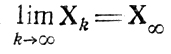
следует

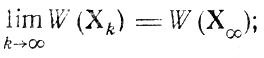
- точечно-множественное отображение W(X_k) называется замкнутым в точке Х_∞, если предельная точка последовательности {X_k+1}, выбираемой в соответствии с требованием k = 1, 2, ..принадлежит W(Х_∞); понятие замкнутости является обобщением понятия непрерывности;

- отображение W(X_k) называется замкнутым на множестве U, если оно замкнуто во всех точках U;

- множество называется компактным, если любая последовательность его точек содержит сходящуюся подпоследовательность;

- если подпоследовательность монотонно возрастающей последовательности {X_k} сходится к некоторой предельной точке Х_∞, то и вся последовательность {X_k} сходится К Х_∞.

Численные методы играют значительную роль в решении важных для практики оптимизационных задач. Это обусловлено целым рядом причин, среди которых главное место занимает разнообразие видов целевой функции z = f(X) и форм ограничений. В отдельных случаях бывает трудно определить, к какому классу относится та или иная задача и существует ли для нее обоснованный метод решения. На выбор метода может влиять стремление максимально использовать мощности ЭВМ с целью снижения затрат на исследования (если подобная перспектива реальна). Большое значение приобретает вычислительный эксперимент как источник информации о свойствах изучаемой задачи (в условиях, когда ее сложность или неопределенность каких-то параметров затрудняют разработку удобной математической модели).

Указанные обстоятельства позволяют рассматривать численные методы оптимизации как необходимое средство решения проблем поиска оптимума в исследованиях, различных по содержанию и сложности.