4.2. Свойства алгоритмических отображений. Теорема сходимости

Пусть решение некоторой экстремальной задачи со скалярным аргументом есть x^* = 0 (в качестве примера здесь можно назвать задачу об отыскании х≥0→min{z = 1+x} или х≥0→max{z = -2х²+3} и т. д.). Если дано исходное значение x = x₁ ≠ 0, то в качестве допустимого можно принять алгоритм, основанный на отношениях x_k+1=x_k/r при r>1 или x_k+1∈[x_k/p, x_k/r] при p>r>1. Как уже отмечалось (см. 4.1), порождаемые подобными алгоритмами последовательности {х_k} обладают свойством

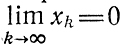
(т. е. сходятся к точке x^* = 0).

Очевидно, далеко не всякий алгоритм является приемлемым в указанном смысле. Так, если

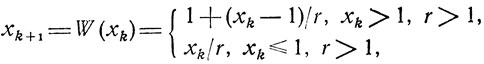(4.1)

то при начальном значении x₁>1 возникает последовательность {х_k}, сходящаяся к Х_∞ = 1. Тот факт, что алгоритм приводит к точке, не удовлетворяющей условию Х_∞ = х^* = 0, равносилен нарушению требования его сходимости.

Чтобы найти причину неудовлетворительного поведения рассматриваемой последовательности, заметим следующее: функция W(x_k) = x_k/r является непрерывной, функция W(x_k) в виде (4.1) имеет разрыв в точке х = 1. Как будет видно из дальнейшего, именно это обстоятельство оказывается решающим для оценок приемлемости того или иного алгоритма.

Пусть алгоритм поиска точки максимума функции z=f (X) на множестве U задан точечно-множественным отображением W(Х_k); пусть далее множество искомых оптимальных X^* не пусто. Обратимся к теореме (11): если

а) все X_k+1, порождаемые принятым отображением W(X_k), образуют компактное множество, включенное в U;

б) для любой точки Х_k+1∈W(Х_k) при Х_k≠Х^* выполнено f(X_k+1)≥f(X_k);

в) при X_k=X^* алгоритм либо завершает поиск, либо для любого X_k+1∈W(Х_k) имеет место равенство f (X_k+1) = f(X_k) = f (X^*);

г) отображение W (X_k) замкнуто в точке X_k при Х_k ≠ Х^*, то рассматриваемый алгоритм либо останавливается в X^*, либо предел любой сходящейся последовательности, формируемой в соответствии с требованием Х_k+1∈W(X_k), есть X^*.

Доказательство: заметим, что здесь достаточно исследовать случай, когда вырабатывается бесконечная последовательность {Х_k} (иначе, в соответствии с условием в), очередная точка Х_k, где завершается поиск,, должна быть принята за X^*); для этого случая можно утверждать сходимость последовательности {Х_k} к Х_∞ (см. условие а)), причем f(Х_k+1)≥f(X_k) и

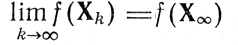
(см. условия б) ив)); рассмотрим подпоследовательность {Х_K+1} с предельной точкой Х_∞+1 в силу тех же замечаний

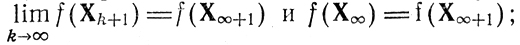
теперь остается лишь убедиться в том, что Х_∞ = Х^*;. предположив противное (т. е. Х_∞=Х^*), приходим к заключению: W(Х_K) замкнуто в Х_∞ (см. условие г)) и f(X_∞+1)≥f(X_∞) при Х_∞∈W(Х_∞) (см. условие б)); но выше было подтверждено, что f(X_∞+1) = f(Х_∞); возникшее противоречие завершает доказательство теоремы. □

Чтобы сделать более конкретным содержание теоремы (11), заметим следующее: если нарушено условие а), то порождаемая алгоритмом последовательность {Х_k} может иметь предельную точку вне U или вообще расходиться; условие б) требует улучшения значений z = f(X) на каждом шаге; условие в) относится к завершающей стадии поиска X^*; условие г) необходимо для обеспечения сходимости алгоритма (в оптимальной точке замкнутость алгоритмического отображения уже не является обязательной, поскольку здесь доминирует требование в)). Таким образом, выбираемое отображение W(X_k) должно обладать целым рядом свойств, перечисленных выше; вследствие этого оно часто имеет весьма сложную структуру.

Непосредственное использование полученных результатов для подтверждения факта сходимости того или иного алгоритма бывает затруднено неудачным выбором W(X_k), который обычно неформален (хотя всегда есть стремление согласовать его с условиями теоремы (11)). Наиболее распространены осложнения, связанные с невозможностью убедиться в наличии свойства замкнутости у W (X_k). В таких случаях может оказаться полезным следующий прием: сложное алгоритмическое отображение разбивается на несколько составных частей,, замкнутость которых доказывается сравнительно легко; затем делается попытка установить желаемое свойство и у первоначального отображения. Реализация этой идеи требует уточнить понятие составного отображения.

Пусть X∈W₁(V) и Y∈W₂(X)-точечно-множественные отображения. Составное отображение W(V) = W₂[W₁(V)] представляет собой объединение множеств W₂(Х), образуемых всеми X, содержащимися в W₁. Например, если W₁(V) и W₂(Х) заданы как [v, 1] и [х-5; x+8], то

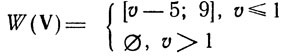
улучай скалярных v, х).

Обратимся теперь к теореме (12), приводимой здесь без доказательства: если W₁(V) замкнуто в точке V_∞, W₂(X) замкнуто на множестве W₁(V) и некоторая подпоследовательность последовательности {Х_k} сходится к Х_∞ при условиях X_kW(V_k), V_k→V_∞, то составное отображение W(V) = W₂[W₁(V) ] замкнуто в W_∞.

Рассмотренные положения позволяют обосновать приемлемость тех или иных численных методов для решения экстремальных задач.