5.4. Дискретная форма задачи. Унифицированный метод решения

Рассмотренные выше активные стратегии поиска х^*, z^* применимы в тех случаях, когда х принимает любые значения на интервале [0, 1]. Возникает вопрос: изменятся ли эти стратегии, если ввести ограничение вида "x может принимать только определенные дискретные значения" или "я может быть только целым числом" и т. д. Чтобы ответить на него, обратимся к изучению одного специфического приема построения схемы поиска экстремума по дискретным точкам. Как будет видно из дальнейшего, предлагаемая стратегия является активной.

Поиск по дискретным точкам

Пусть х принимает какие-то значения х₁, х₂, ...,x_M^* из [0, 1], причем их число конечно. Считая, что нумерация этих значений проведена в порядке их возрастания (рис. 5.17), введем в рассмотрение новую переменную y, которая может принимать только целые значения 1, 2,.... Поскольку номера точек, отмеченных на оси х, совпадают с первыми М^* значениями y, можно поставить в однозначное соответствие этим у величины z_y (y = 1,....,M^*), которые будут найдены в точках х_y. Другими словами, можно перейти от рассмотрения функции z = f(x) к рассмотрению z_y = f_y(y).

Будем считать, что для решения задачи поиска в этих условиях используется метод чисел Фибоначчи. Отметим на оси у ряд точек с координатами M+1, М^*+2, ..., М, выбрав их количество М-М^* так, чтобы число М+1 оказалось ближайшим к М^* числом Фибоначчи (в частном случае может быть М = М^*). Значения z_y в указанных точках не определяются, поэтому сами точки называются фиктивными. Таким образом, приходим к задаче: на оси y задан интервал длиной M + 1 = Fη, содержащий М целочисленных положительных значений y (y = 1,...., М), и требуется среди первых М^* точек у найти такую, в которой zy достигает максимума.

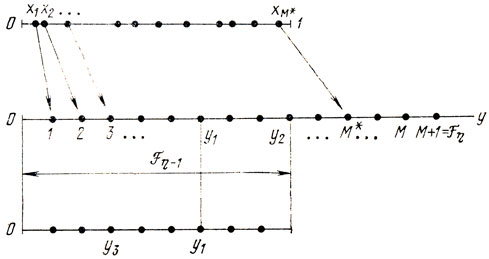
Рис. 5.17

Оказывается, решить поставленную задачу выбранным методом можно, если в общих формулах (5.7), (5.8) положить ε = 0 и N = η. Начнем с выбора первой точки y₁; она определится здесь равенством y₁ = (1-L₂)F_η которое учитывает имевшее место (при переходе от х к y) увеличение F_η в раз длины исходного интервала неопределенности. Обращаясь к выражению L₂ и полагая ε = 0, получаем y₁ = F_η - F_η-1(при N=η). В силу дело численности F_η и F_η-1 найденное значение y₁ будет тоже целочисленным, поэтому точка y₁ и симметричная ей точка y₂ займут те положения на оси y, которые допустимы по условиям исходной задачи. При этом длина нового интервала неопределенности составит F_η-1 (он будет слева, если y₂ окажется среди фиктивных точек) и вся ситуация повторится (точка y₃, симметричная y₁ в интервале F_η-1 обязательно займет допустимое положение). Наконец, по окончании всех η эксперименте, останется интервал неопределенности равный 1, так как L_N = 1/F_N при ε = 0.

Все отличия рассмотренной схемы поиска х^* от схемы чисел Фибоначчи заключаются в необходимости проведения небольшой предварительной подготовки. В дальнейшем, при анализе более общих задач, будут использованы основные понятия этой главы и принципы построения простейших стратегий поиска х^*, z^*. Ниже даны иллюстративные примеры.

Пример: найти точку экстремума (максимума) унимодальной функции

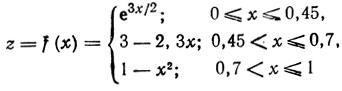
методом дихотомии при ε = 0,04 и N = 8.

Решение: а) выбираем точки x₁ = 0,5-ε/2 = 0,48 и x₂ = 0,5+ε/2 = 0,52; для них z₁ = 1,896 и z₂ = 1,804; поскольку z₁>z₂ для дальнейшего анализа остается интервал [0; 0,52] с центром в х = 0,26;

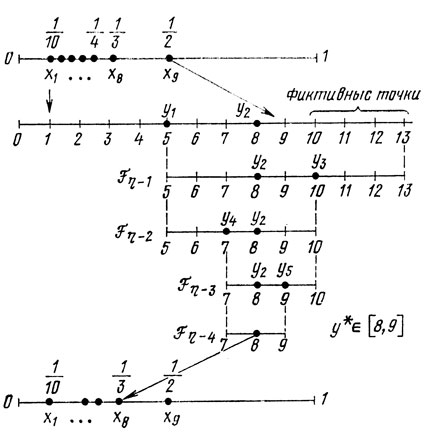
Рис. 5.18

б) выбираем новые точки x₃ = 0,26-ε/2 = 0,24 и x₄ = 0,26+ε/2 = 0,28; здесь z₃ = 1,433 и z₄ = 1,522, поэтому остается [0,24; 0,52] с центром в x = 0,38;

в) теперь исследуем точки x₅ = 0,38-ε/2 = 0,36 и x₆ = 0,38+ε/2 = 0,40, для которых z₅ = 1,716 и z₆ = 1,822 (z₆>z₅); следовательно, сохраняется интервал [0,36; 0,52] с центром в x = 0,44;

г) последние точки есть x₇ = 0,42, x₈ = 0,46; им соответствуют z₇-1,877 и z₈ = 1,993 (z₈>z₇); это дает интервал неопределенности [0,42; 0,52] длиной

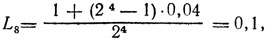
так что 0,42≤x^*≤0,52.

Если дополнительно использовать информацию, получаемую из сравнения z₁ с z₇ и z₈ (z₇<z₁<z₈ при x₇<x₈<x₁), то можно утверждать: 0,42≤x^*≤0,46 и z^*≤1,993 (интервал L₈ уменьшился до 0,04 без изменения N).

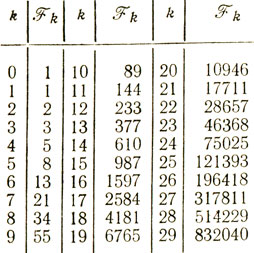
Таблица чисел Фибоначчи

Пример: найти точку экстремума (максимума) унимодальной функции z = f(x) = x(0,366-0,515x) на дискретном множестве точек х = { 1/10, 1/9, 1/8, 1/7, 1/6, 1/5, 1/4, 1/3, 1/2}.

Решение: здесь М^* = 9 и ближайшее (сверху) к М^* число Фибоначчи есть F₆ = 13 (следовательно, η = 6); целочисленный параметр у меняется в пределах 0-13 (см. рис. 5.18);

а) выбираем точку y₁ = (1- L₂F_θ = F₆ = F₅ = 5 (см. таблицу чисел Фибоначчи); из изображений симметрии y₂ = 8, поэтому z₁ = f(x₅) = 0,0466, z₂ = f(x₈) = 0,0645, и для дальнейшего рассмотрения остается интервал [5, 13];

б) на интервале [5, 13] сохраняется точка y₂ = 8 (этого требует метод Фибоначчи), отсюда y₃ = 10 (фиктивная точка); поскольку f_y не определяется в фиктивных точках, интервал (10,13] отбрасывается (рис. 5.18);

в) в оставшемся интервале [5, 10] присутствует y₂ = 8, так что y₄ = 7; из сравнения z₄ = 0,0418 с z₂ = 0,0645 следует оценка: y^*∈[7, 10];

г) назначаем y₅ = 9, т. е. z₅ = 0,0542 и z₅<z₂; остается исследовать интервал [7, 9], в разрешенных точках которого уже известны значения 2 (это 24, 22, 25); наибольшим здесь является z₂ = 0,0645, поэтому x^*≈1/3, z^* = 0,0645.

Полезно заметить, что длина каждого очередного интервала неопределенности в схеме, показанной на рис. 5.18, представляет собой число Фибоначчи; в заключительной фазе поиска сказывается влияние граничных условий F₀ = F₁ = 1.

Пример: найти точку экстремума (максимума) унимодальной функции

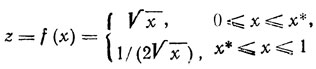
Методом золотого сечения при ε = 0,05 и N = 5 (предполагается, что х^*∈[0, 1]).

Решение: а) в соответствии с общими рекомендациями метода (рис. 5.16) выбираем x₁ = 0,382 и х₂ = 0,618; чтобы определить z₁ в рассматриваемой задаче, достаточно взять меньшее из чисел

√0,382 и 1/(2√0,382 (им является √0,382 = 0,62, рис. 5.19); точно так же

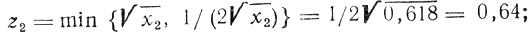
>z₁ дальнейшему изучению подлежит интервал [0,382; 1], в котором находится

б) значение х₃ есть 0,764, следовательно,

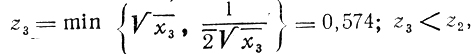
остается интервал [0,382; 0,764];

в) значение х₄ есть 0,528, следовательно,

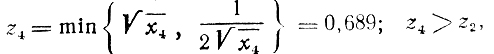
оставляем интервал [0,382 0,618];

г) значение х₅ есть 0,472 и z₅ = 0,688 < z₄; длина интервала неопределенности [0,472; 0,618], полученного в результате всех пяти экспериментов и содержащего точку х^*, составляет L₅ = 1/τ⁴=0,146, причем z^*≥0,689.

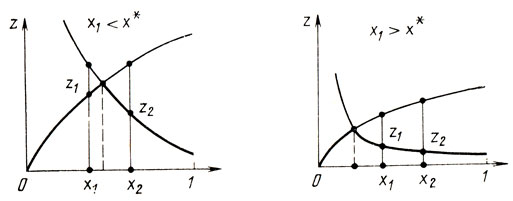
Рис. 5.19

Необходимо обратить внимание на специфику рассмотренной задачи, в которой схема поиска экстремума была косвенно использована для решения уравнения √x-(2√x)^-1 = 0. Это расширяет области приложения изучаемой теории, активно используемой и при формировании стратегий многомерной оптимизации.