5.3. Активные стратегии поиска. Эффективность устранения исходной неопределенности

Способы организации поиска х^*, z^*, рассмотренные в § 5.2, предполагали выбор сразу всех N значений х, что можно считать серьезным недостатком. С этой точки зрения всякая стратегия, предусматривающая последовательное (пошаговое) проведение опытов и оценку возникающих ситуаций, представляется более прогрессивной, так как позволяет экономить средства и время, с расходованием которых неизбежно связана постановка эксперимента. Именно это характерно для активных стратегий, изучаемых ниже. Полезно отметить, что они тоже являются ε-минимаксными.

Метод дихотомии

Метод дихотомии (половинного деления)-один из самых простых методов поиска. Его идея и содержание заключаются в следующем: из N экспериментов, находящихся в распоряжении исследователя, выбираются два (х₁, х₂) и размещаются на исходном единичном отрезке наилучшим (в смысле критерия L₂) образом, т. е. симметрично относительно середины отрезка на расстояниях ε/2 от нее (рис. 5.9). В результате сравнения полученных величин z₁ и z₂ становится возможным указать гарантированный интервал неопределенности L₂₍₁₎ = (1+ε)/2 (будем считать, что он смещен влево). Получив таким образом L₂₍₁₎, можно повторить применительно к нему всю описанную процедуру, используя для этого вторую пару (x₃, х₄); это даст новый интервал неопределенности L₂₍₂₎ = (L₂₍₁₎+ε)/2 = (1+3ε)/4, положение которого связывается с серединой отрезка L₂₍₁₎. Затем наступает очередь следующей пары (x₅, x₆), размещаемой у середины L₂₍₂₎ и позволяющей получить L₂₍₃₎ = (L₂₍₂₎ + ε)/2 = (1+7ε)/8. Процесс продолжается до тех пор, пока не будут проведены два последних эксперимента в x_N-1 и x_N; длина оставшегося интервала неопределенности, характеризующая эффективность метода, есть

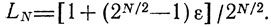(5.6)

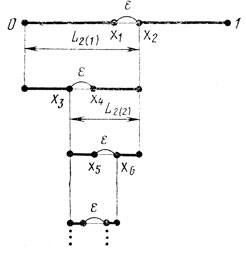
Рис. 5.9

Особенностью рассматриваемой схемы является то, что эффективность использования очередной пары экспериментов снижается по сравнению с эффективностью предыдущей пары. Действительно, если к некоторому моменту окажутся "израсходованными" η пар, η<N/2, то величина интервала неопределенности составит

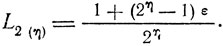
Если мы попытаемся использовать еще одну пару, то получим

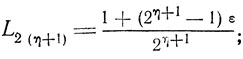
тем самым интервал L_2(η) уменьшается на величину

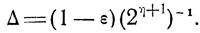
Нетрудно видеть, что выигрыш Δ тем меньше, чем больше η (т. е. номер пары); в пределе (при η→∞) этот выигрыш стремится к нулю, хотя теоретически возможность размещения очередных пар сохраняется всегда (практически же не имеет смысла использовать более 7-8 пар).

Представляет интерес сравнительная оценка результатов (5.6) и (5.5). В качестве ее основы можно принять соотношение между числами экспериментов, необходимых для получения одинаковых L_N в схемах поиска, изображенных на рис. 5.7, 5.9. Из равенства правых частей формул (5.6) и (5.5) следует

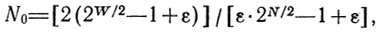
где N₀ - новое обозначение числа экспериментов в формуле (5.5). Графики зависимости N₀ от N, построенные для разных значений е, приведены на рис. 5.10. Они показывают, что затраты усилий (т. е. величина N₀) при использовании пассивной стратегии тем больше, чем меньше ε и больше N; например, При N = 6 и ε = 0,05 величина N₀ приблизительно в 2 раза превышает N, а при N = 10 и ε = 0,02 требуется провести порядка 40 "пассивных" экспериментов, что-бы получить тот же результат L_N. Полезно заметить, что эффективность метода дихотомии снижается с увеличением ε.

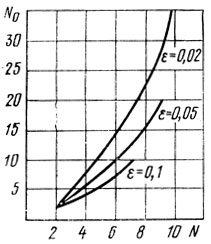
Рис. 5.10

Преимущества метода дихотомии заключаются в предельной простоте, однако существуют более совершенные активные стратегии.

Метод чисел Фибоначчи

Реализация этого метода связана с использованием последовательности целых чисел, открытой итальянским математиком Леонардом Пизанским (Фибоначчи) в начале XIII века. Чтобы проследить за ходом развития схемы поиска х^*, z^*, предположим, что в нашем распоряжении имеется, как обычно, N экспериментов. Оценим ситуацию, которая возникает после того, как в соответствии с некоторой ε-минимаксной стратегией проведен N-1 эксперимент и остается выбрать последнее значение x = x_N. К этому моменту гарантированная длина интервала неопределенности становится равной L_N-1 а сам интервал содержит точку X_N-1 (рис. 5.11), причем среди всех величин z_q(q = 1,..., N-1), полученных в предшествующих экспериментах, наибольшей является именно z_N-1. Положение x_N-1 на отрезке L_N-1 зависит от того, какая стратегия была реализована на предыдущих шагах.

Длина конечного интервала неопределенности будет определяться не только выбираемым x_N, но и уже имеющимся x_N-1. Очевидно, результат поиска окажется наилучшим в смысле (5.2) только тогда, когда x_N-1 расположится на расстоянии ε/2 от середины L_N-1 (рис. 5.11) (в этом случае достаточно разместить точку x_N симметрично x_N-1 и найти L_N = (L_N-1 + ε)/2 независимо от того, в каком отношении находятся z_N и z_N-1). Таким образом, первым требованием к исследуемой схеме является следующее: после проведения N-1 экспериментов точка x_N-1 должна занять на L_N-1 положение, указанное на рис. 5.11 (естественно, в ходе экспериментов допускается перенумерация точек).

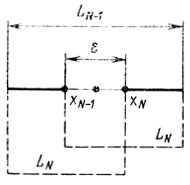
Рис. 5.11

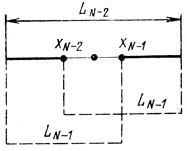
Рис. 5.12

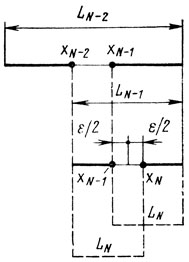
Рис. 5.13

Пусть теперь стоит задача выбора двух последних значений х (x_N-1 и x_N) в условиях, когда N-2 эксперимента проведены и найден интервал L_N-2, содержащий точку x_N-2, в которой получено значение z = z_N-2, наилучшее (по смыслу задачи) в рассматриваемой серии опытов (рис. 5.12). Начнем выбирать x_N-1 (внутри L_N-2); как только x_N-1 и соответствующее z_N-1 станут известны, можно будет указать новый интервал неопределенности, меньший L_N-2. Поскольку заранее нельзя предсказать, будет ли z_N-1>z_N-2. лучше всего расположить точку x_N-1 симметрично x_N-2 несмотря на то, что расстояние между x_N-1 и x_N-2 окажется наверняка больше ε. Предложенный выбор х_N-1 дает гарантию того, что длина нового интервала неопределенности не превысит величины L_N-1, отмеченной на рис. 5.12, причем L_N-1 не может быть уменьшена, если задана точка x_N-2 (т. е. L_N-1 является минимаксом). Зная теперь x_N-1 и помня о требовании, отраженном в рис. 5.11, приходим к выводу: чтобы получить результат L_N, необходимо два последних эксперимента провести так, как показано на рис. 5.13, выполнив тем самым условие L_N-2 = L_N-1 + L_N.

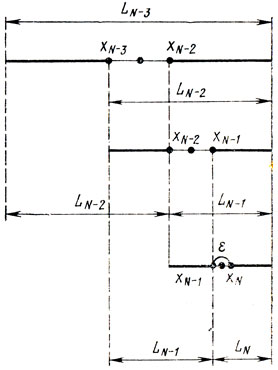
Рис. 5.14

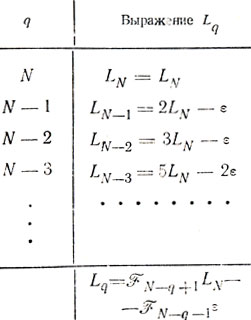
Таблица 5.1

Если сделать очередной шаг и поставить задачу: найти x_N-2, x_N-1, x_N при известных L_N-3, x_N-3, z_N-3, то окажется, что рассуждения, приведенные выше, могут быть целиком перенесены и на этот случай. Таким образом, приходим к равенству L_N-3 = L_N-2 + L_N-1 далее схема строится так, как показано на рис. 5.14.

Теперь ясно, что основное соотношение, характеризующее изучаемый метод, имеет вид

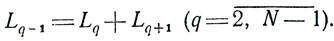(5.7)

Его анализ удобно начать с конкретизации выражений L_q(q = N, N-1, ...), сведя их в табл. 5.1.

Нетрудно заметить, что коэффициенты при L_N и ε в формулах таблицы составляют последовательность чисел Фибоначчи, задаваемую равенствами F₀ = F₁ = 1, F_k = F_k+1+F_k-2, где k - номер числа, принимающий значения 2, 3, ... Используя это обстоятельство, можно дать общую запись выражения L_q приведенную в нижней строке табл. 5.1, откуда следует L₁ = F_NL_N-εF_N-2. Но L₁ есть исходный единичный интервал неопределенности (L₁ = 1), поэтому

Соотношение (5.8) позволяет оценить эффективность метода чисел Фибоначчи (прежде всего в сравнении с методом дихотомии). Приравнивая правые части формул (5.8), (5.6) и обозначая N в (5.6) как N_д, получаем

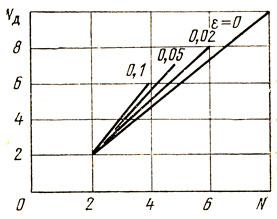
Рис. 5.15

Кривые N_д = N_д(N), построенные для разных значений ε, показаны на рис. 5.15; легко видеть, что разница в числах N здесь не такая большая, как на рис. 5.10. Например, при N = 5 и ε = 0,05 N_д = 7 (в схеме дихотомии требуется затратить всего на два эксперимента больше, чтобы получить тот же результат поиска). Приблизительно те же соотношения сохраняются и для других значений ε. Это объясняется существованием при каждом ε = const предельного числа N, которое может быть найдено из условия: длина конечного интервала не определенности Ln не должна быть меньше 2ε, следовательно, F_N+1≤1/ε (например, для ε = 0,02 F₈<1/ε, по F₉>1/ε, т. е. искомое N_иред = 7). Таким образом, в диапазоне реальных значений N (от 4-5 до 25-30) отношение (N-N_д)/N_д колеблется в пределах 0,2-0,3. Большая эффективность метода чисел Фибоначчи связана с тем, что сокращение длины очередного интервала L_q требует проведения одного нового эксперимента, тогда как в схеме дихотомии их требовалось два.

В заключение рассмотрим вопрос о выборе точки x₁ и связанной с этим возможностью реализации метода. Из предыдущего анализа следует х₁ = 1-L₂; но L₂ = F_N-1L_N-εF_N-3 (см. табл. 5.1) или с учетом (5.8) L₂ = F_N[F_N-1+ε(F_N-1F_N-2-F_NF_N-3)]. Отсюда следует, что сделать первый шаг здесь можно лишь тогда, когда назначено число N, т. е. x₁ = x₁ (N). Это является недостатком, затрудняющим в ряде случаев решение задачи из-за невозможности изменить N после начала экспериментов. Всегда желательно располагать стратегией, не требующей предварительного задания N, но приближающейся по своей эффективности к исследованному методу чисел Фибоначчи.

Метод золотого сечения

Выше было показано, что использование рекуррентного соотношения (5.7) в качестве основы для построения схемы поиска х^*, z^* оказывается весьма эффективным. Можно ожидать, что ориентация на разные начальные условия позволит найти в рамках этого соотношения разные схемы поиска, каждой из которых присущи свои особенности, но всем им - достаточно высокая эффективность.

Рассмотрим величину τ = L_q-1/L_q и потребуем ее постоянства при разных q одновременно с выполнением условия (5.7). Разделим обе части (5.7) на L_q+1>0, указав тем самым уравнение τ² = τ+1, которому должно удовлетворять τ (здесь τ² = L_q-1/L_q+1). Положительный корень этого уравнения есть τ = (1+√5)/2≈1,618; зная его, можно построить последовательность экспериментов, начиная с x₁ = 1 - 1/τ = 0,382 (рис. 5.16), и прийти в конце концов к интервалу неопределенности

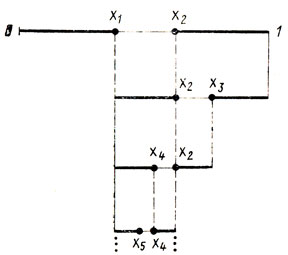
Рис. 5.16

Проводить эксперименты здесь можно до тех пор, пока выполняются совместно условия (5.9), L_N-1 = τL_N, L_N≥0,5 (L_N-1 + ε), откуда следует N≤1 + [lg(2-τ) - lgε](lgτ)^-1. Например, для ε = 0,02 получаем N_пред = 6.

Сравнение результатов (5.9) и (5.8) можно провести, приняв за основу отношение соответствующих величин L_N при одинаковых N (обозначим его как L). Разделив, почленно (5.9) на (5.8), получим L = F_N/((1 + εF_N-2)τ^N-1). Очевидно, наибольшие значения L принимает при ε = 0, причем, начиная с N = 4, оно стабилизируется около 1,17. Таким образом, с точки зрения эффективности метод золотого сечения занимает промежуточное положение между методами дихотомии и чисел Фибоначчи.