6.2. Выбор начальных условий поиска. Линейная модель поверхности отклика

Здесь будут рассмотрены вопросы, касающиеся выбора исходной опорной точки Х₀ и содержания исследований на этапе I поиска X^*, z^*. В общем случае затраты средств и времени, с которыми неизбежно связана постановка экспериментов, могут быть сокращены удачным выбором Х0. Пусть в области эксперимента (Э) указаны две точки - точка У, которую достаточно обоснованно можно назвать центром области, и точка 2, расположенная на периферии (рис. 6.1). Обе они могут выступить в роли Х₀, однако опасность растянуть процесс решения задачи (перерасходовав тем самым материальные средства) оказывается большей для точки 2. Причина этого заключается в возможности появления X^* на "противоположной стороне" области Э и связанного с этим увеличения количества переходов, составляющих процесс поиска. Следовательно, всегда желательно выбирать Х₀, используя понятия центра области. Ниже приведены три определения центра, которые могут быть полезны на практике.

I. Предположим, что в качестве характеристики области Э принят перечень величин

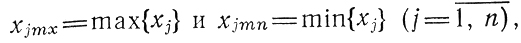
определяющий ее "габаритные" размеры и содержащий 2n чисел (рис. 6.2); точка Х_с с координатами x_jc = 0,5(x_jmn+x_jmn) (j = 1,...,n) называется средней точкой и может рассматриваться как центр области; достоинством такого определения является простота, недостатки же заключаются в возможности попадания Х_с за пределы Э (если, например, область имеет кольцеобразную форму), а также в чувствительности к поворотам координатной системы.

II. Пусть в области эксперимента выбрана некоторая точка X; гиперплоскость, являющаяся касательной к поверхности уровня z = const в этой точке, делит Э на две части с объемами v₁, v₂ всегда можно считать v₁≤v₂, см. рис. 6.3). Величины v₁, v₂ зависят о от положения X и направления вектора градиента v₁(X), т. е. v₁ = v₁(X, ∇) и v₂ = v₂(X, ∇).

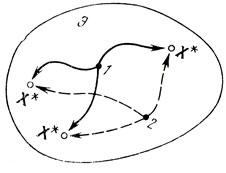
Рис. 6.1

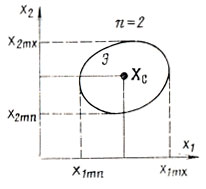
Рис. 6.2

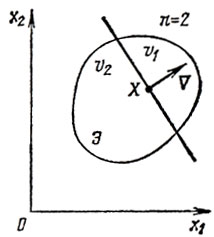
Рис. 6.3

Критерием сравнения X с другими точками области Э может служить величина v

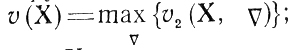
это позволяет рассматривать точку Х_мм с характеристикой

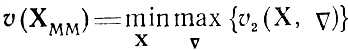
в качестве искомого центра области (минимаксный центр). Он нечувствителен к поворотам и параллельным переносам координатной системы, однако трудности его вычисления весьма велики (особенно в случаях, когда область Э имеет сложную форму и n<3).

III. Часто оказывается удобным использовать понятие центра тяжести (Х_цт), связывая его с представлением области эксперимента как некоего однородного тела; все необходимые вычисления проводятся по известным формулам механики (их можно найти в примере на с. 186).

Приведенные определения центра не исчерпывают всех возможных определений. Точки Х_с, Х_ММ, Х_цт и другие выполняют функции исходных опорных точек не только на первом шаге поиска (здесь они обозначаются как Х₀), но и на последующих шагах, если, конечно, имеющаяся (или появляющаяся) в распоряжении исследователя информация о свойствах z = f(X) не отвергает самой идеи использования понятия "центр" в подобных целях.

Обратимся теперь к анализу этапа I, считая, что точка Х₀ с координатами х₁₀, x₂₀,....,x_n0 по так или иначе выбрана и в ней определено опытным путем значение z₀ = f(x₁₀, x₂₀, ...., x_n0). Этот единственный пока эксперимент не дает никаких сведений о характере поверхности отклика в окрестности Х₀ (а также о направлении дальнейшего "движения"). Чтобы получить нужную информацию в существующих условиях неопределенности, приходится строить более или менее приближенную модель исследуемого участка рассматриваемой поверхности. В качестве основы здесь может быть принята формула Тейлора

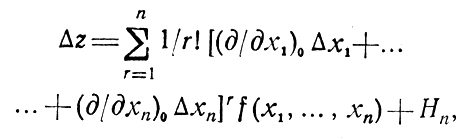(6.1)

позволяющая оценить приращение Δz, которое будет получено при переходе из Х₀ в какую-то другую точку X. Для вычисления частных производных, входящих в (6.1), используется первая группа пробных экспериментов, проводимых "вблизи" Х₀. Их число определится количеством членов разложения (6.1), причем обычно оставляется его линейная часть

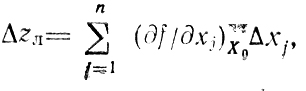
что позволяет разумно Сократить объем работы и в то же время получить приемлемый результат. Здесь достаточно вычислить только первые производные, и пробные эксперименты проводятся в точках (х_10+ε, x₂₀,....,x_n0), (x₁₀, x_20+ε, x₃₀, . . ., x_n0),....., (x₁₀, . . ., x_n0+ε), находящихся на расстоянии ε от Х0 (смысл величины ε в данном случае тот же, что был при анализе простейших схем поиска, см. гл. 5). Соответствующие величины z_jε (j = 1,...,n) входят в оценочные формулы

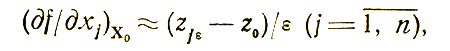
позволяющие, в свою очередь, найти Δz_л при различных вариациях значений Δx_j. Знак и величина Δz_л определят направление следующего шага (этим завершается этап I поиска X^*, z^*).