6.3. Оценка результатов исследований. Нелинейные модели поверхности отклика

Теперь остается рассмотреть этап III. Здесь тоже предполагается проведение локальных исследований поверхности отклика, но в окрестности точки X^*. Чтобы пояснить, зачем нужно исследовать точки "вблизи" X^*, если X^* (и, конечно, z^*) уже получены, заметим следующее:

- найденная точка X^* может оказаться ложной вследствие погрешностей вычислений, проводимых в процессе поиска, а также незнания каких-то особенностей функции z = f(Х);

- экстремум z может оказаться слабым относительным максимумом или минимумом, и существует множество точек Х°, в которых z принимает то же значение, что и в X^*;

- иногда величины х^*₁, х^*₂, ..., х^*_n, определяющие X^*, z^*, оказываются неприемлемыми с точки зрения затрат, необходимых для практической реализации найденного решения, и тогда возникает задача оценки размеров проигрыша, связанного с отказом от X^* (подобная ситуация часто возникает на ранних стадиях проектирования систем).

Так же, как и на этапе 1, для построения модели участка поверхности z = f(X) используется разложение (6.1), однако ограничиться анализом только линейной его части не удается (первые Производные обращаются в нуль в точке X^*). Ясно, что с увеличением порядка сохраняемых членов формулы (6.1) растут вычислительные трудности, объем работы и, как правило, снижается точность расчетов. Если нет особых причин для учета слагаемых высших порядков, то следует попытаться в первую очередь оценить допустимость так называемой квадратичной аппроксимации f(X), выраженной в формуле

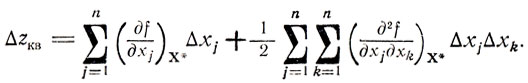(6.2)

В (6.2) входят n + 0,5n(n+1) слагаемых. Для определения их коэффициентов нужно провести многочисленные эксперименты и расчеты, поэтому естественно стремление еще более сократить выражение (6.2), оставив в нем для начала только те слагаемые, которые не содержат смешанных частных производных, т. е. рассмотреть равенство

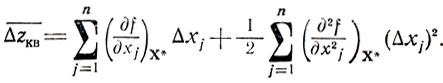(6.3)

Формула (6.3) определяет аппроксимацию, не учитывающую связей между переменными, и включает только 2n слагаемых, что дает заметный выигрыш в количестве подсчитываемых коэффициентов, однако существует опасность того, что значения вторых смешанных производных, которыми пренебрегли при переходе от (6.2) к (6.3), окажутся в действительности довольно большими, и это приведет к искажению результатов.

Чтобы оценить, насколько приемлема аппроксимация (6.3), нужно решить систему n уравнений вида

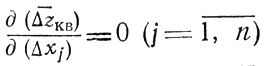
и получить тем самым значения приращений Δx̄₁, Δx̄₂,.....,Δx̄_n, определяющие некоторую точку X^** (рис. 6.4). Чем дальше находится X^** от X^*, тем больше оснований считать аппроксимацию (6.3) неудачной. При Δx̄_j ≤ε(j = 1,...,n) точки X^** и X^* становятся практически неразличимыми, и формула (6.3) может быть принята; если же Δx̄_j>ε (для всех или части номеров j), вопрос о допустимости (6.3) решается применительно поверхность к конкретным условиям задачи.

Предположим, что произошло худшее и пришлось отказаться от (6.3). Обращаясь вновь к приближению (6.2), видим, что последовательность действий сохраняется здесь полностью: решается система уравнений d(Δz_KB)/d(Δx_j) = 0 (j = 1,...,n), отыскиваются поправки Δx̄_j (j = 1,...,n), определяющие точку X^**, дается заключение о допустимости формулы (6.2) (для этого необходимо рассчитать дополнительно 0,5n (n-1) коэффициентов).

Полезно обратить внимание на одно осложнение, которое может возникнуть при таких проверках. Иногда при допустимых Δx̄_j значения z в точках X^* и X^** заметно отличаются друг от друга (например, из-за неточности вычислений величина г^*, найденная экспериментально, и величина z^**, подсчитанная по приближенной формуле, не могут быть признаны хотя бы приблизительно равными). Поэтому желательно организовать дополнительную проверку точек, близких к X^*, основанную на сравнении значений 2, полученных опытным путем и рассчитанных (для тех же X) по формулам (6.3) или (6.2).

Пусть необходимый анализ аппроксимации (6.2) проведен и дал положительный результат - заключение о ее пригодности (в противном случае пришлось бы заняться разложением, содержащим члены порядка 3 и т. д.). В чем должен выражаться факт принятия (6.2)? Во-первых, в корректировке положения X^* в соответствии с имеющимися Δx̄_j (j = 1,...,n), т. е. в замене участка реальной поверхности отклика его моделью, построенной на основе использования формулы (6.2), после чего точкой экстремума становится X^**. Во-вторых, в использовании для дальнейших исследований разложения 2 в окрестности X^**, вытекающего непосредственно из принятой модели,

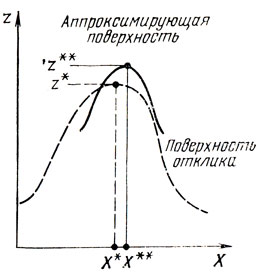
Рис. 6.4

Изучив вопрос о допустимости той или иной формы аппроксимации z, следует выяснить, является ли точка X^** заменившая X^*, действительной точкой экстремума. Если это так, то любые отклонения x_j(j = 1,...,n) от значений х^** (j = 1,...,n), определяющих X^**, должны приводить лишь к неблагоприятным изменениям величины z = z^** (в противном случае найдутся такие Δx_j, которые не приведут к указанным изменениям z^** и, более того, могут "улучшить" z). Таким образом, здесь приходится исследовать достаточные условия экстремума: если z, заданная своим разложением, отрицательно (положительно) определена в некоторой окрестности X^**, то X^** является точкой максимума (минимума) z если же это требование не выполнено, необходимо искать новую точку X^* и, следовательно, новую X^**.

После того как заключительные исследования проведены и оказалось, что в X^** экстремум есть, заканчивается этап III поиска.

Чтобы иметь возможность перейти к изучению конкретных стратегий поиска X^*, z^*, необходимо ввести некоторые определения (они формулируются для max z).

Рассматривая систему параметрических уравнений х₁-х₁(t), х₂ = х₂(t), ..., x_n = x_n(t), можно говорить о кривой (или траектории), заданной этими уравнениями в R_n и соединяющей какие-то точки Х_А, Х_В; им (как и любым другим точкам траектории) отвечают значения z, которые могут быть найдены экспериментально. Поскольку разным t соответствуют разные точки, зависимость z = f(x₁, x₂, ..., х_n), отнесенная к произвольно выбранной траектории, переходит в z = f(t).

Если из условия t₁>t₂ следует z(t₁) >z(t₂), то траектория называется строго возрастающей. Функция z = f(Х) называется унимодальной, если для любой точки Х∈Э найдется строго возрастающая траектория, идущая в X^*. В случаях, когда такая траектория прямолинейна, f(X) является строго унимодальной функцией. Наконец, если f(X)-унимодальная (в смысле определения, данного в гл. 5) на произвольной прямой в Э, то имеет место линейная унимодальность f(X).

В дальнейшем будет использовано и понятие поверхности уровня как множества точек X, удовлетворяющих равенству z = f (X) = const (при n=2 она вырождается в линию).