7.2. Методы стохастической аппроксимации. Специфика условий сходимости

В историческом плане возникновение прикладных методов стохастической аппроксимации связано с именами Роббинса и Монро, которые предложили схему поиска корня функции в условиях помех. Хотя задача такого рода не является непосредственно оптимизационной, она хорошо иллюстрирует основные положения, сформулированные выше.

Процедура Роббинса-Монро

Пусть априори известно, что z_и<0 при x<x^*, z_и>0 при x>x^*, z_и = 0 при х = х^* (рис. 7.1). Характеристики ошибок, искажающих результаты определения z при тех

или иных x_i, предполагаются следующими:

- математическое ожидание δ_zi равно нулю для любого i (i = 1, 2, .. .);

- дисперсия δ_zi конечна и постоянна при различных i;

- величины δ_zi, присутствующие в разных экспериментах, независимы и носят аддитивный характер.

Предлагается схема переходов. X_i+1=x_i-a_iz_i, где z_i - значение z в точке хи найденное экспериментально; а_i - член последовательности корректирующих коэффициентов. Требуется дать оценку сходимости процесса, реализуемого в соответствии с этой схемой.

Поскольку z_i = z_иi-δ_zi, можно представить X_i+1 как Х_i+1 = (x_i-a_iz_иi)-a_iδ_zi, откуда следует Y_i = x_i-a_iz_иi, R_i = -a_iδ_zi. Обращаясь к условиям сходимости процесса в средне-квадратическом, рассмотрим две группы соотношений для R_i и Y_i.

Анализ случайной составляющей: из выражения R_i и исходных предпосылок получаем М [R_i] = - aМ [δ_zi] = 0, D[R_i] = M[R_i²] = a²_iD[δ_zi], где D[δ_zi] есть дисперсия ошибки, не меняющаяся с изменениями i. Ясно, что требование

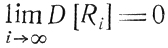
в данном случае удовлетворяется, если

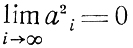
или

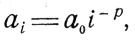
где а₀ - некоторая константа; р - показатель степени, выбираемый как p≥0,5.

В рамках этих условий нетрудно получить и

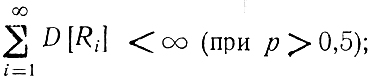
таким образом, проблема фильтрации ошибок решается здесь в принципе просто.

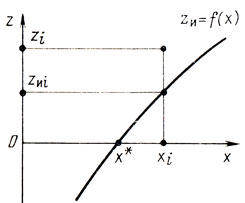
Рис. 7.1

Анализ регулярной составляющей удобно провести применительно к случаям а), б), рассмотренным в § 7.1. 15 8

Модуль разности Y_i-х̂ = х_i-a_iz_иi-x̂ может быть представлен здесь как

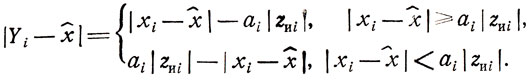(7.1)

Если сделать те или иные предположения о характере

зависимости z_иi от x_i (или, что то же, от г), то формула (7.1) позволит оценить, насколько реально выполнение

условия

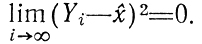
Пусть, например, существует возможность указать для очередного х_i нижнюю границу значений |z_иi| т. е. принять |z_иi|>ρ_i. Это значит |Y_i-x̂|<|x_i-х̂|-а_iρ_i [см. верхнюю строку (7.1)]; слагаемое -a_iρ_i может рассматриваться как поправка -γ_i (см. 7.1), если только последовательность {а_iρ_i} обладает свойством

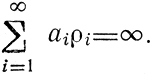
Точно так же, допуская |z_иi|≤A|х_i-х̂|+В, где А и В - некоторые константы, получаем |Y_i-x̂|<а_iВ+(a_iA-1)|x_i-x̂| [см. нижнюю строку (7.1)]. Начиная с некоторого номера i, разность

a_iA-1 станет отрицательной (с каждым шагом коэффициент a_i уменьшается), и тогда последнее неравенство

примет вид |Y_i-х̂|<a_iB; очевидно,

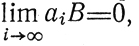
и величина Y_i сходится к x̂.

Таким образом, процедура Роббинса - Монро обеспечивает выполнение условий сходимости, хотя и предъявляет определенные требования к уровню информированности исследователя о свойствах функции z_и = f(x).

Все сказанное выше основывается на результатах теоремы Дворецкого (16), приводимой здесь без доказательства: пусть {α_i}, {β_i}, {γ_i} - последовательности неотрицательных действительных чисел, такие, что

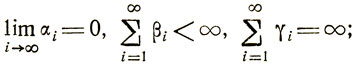
пусть х̂ - действительное число, a Y_i- измеримые преобразования, удовлетворяющие условию |Y_i-x̂|≤max{α_i, (1 + β_i)|x_i-х̂|-γ_i} для всех действительных x_i (i = 1,2,...); пусть далее X_i+1 = Y_i+R_i, где R_i - действительные случайные величины, причем M[R_i] = 0,

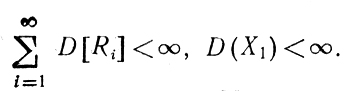
В этих предположениях схема Роббинса-Монро обеспечивает сходимость процесса оптимизации в среднеквадратическом (и по вероятности) к х̂.

Обратимся теперь к анализу еще одного метода стохастической апппроксимации, предназначенного специально для поиска максимума f(x).

Процедура Кифера - Вольфовица

Допустим априори, что функция z_и = f(x) унимодальна и имеет экстремум (максимум) в точке х^*. Ошибки, искажающие результаты экспериментов, имеют следующие особенности:

- они аддитивны;

- математическое ожидание δ_zi = 0 для всех i (i = 1, 2, ...);

- дисперсия δ_zi конечна и постоянна (t = 1, 2, ...);

- случайные величины δ_zi и δ_zk (i = k) независимы.

Предлагается схема переходов: X_i+1 = X_i+a_i[z(x_i+с_i) - z (х_i-c_i)/с_i, где z(x_i+c_i) и z(x+c_i)-значения z в точках x_i-соответственно; a_i и c_i-члены последовательностей неотрицательных действительных чисел. Требуется дать анализ сходимости предложенной схемы.

Геометрическая интерпретация рассматриваемых условий дана на рис. 7.2; величина [z(x_i+с_i) - z(x_i-c_i)](2c_i)^-1 определяет приближенно тангенс угла наклона кривой z_и = f(x) в точке х_i (для этого на каждом шаге проводятся два эксперимента). Таким образом, идея метода заключается в последовательных оценках величин θ_i с целью выбора направления дальнейшего "движения". Учитывая, что z(x_i±c_i) = z_и(x_i±c_i) + δ_z(x_i±c_i) получаем

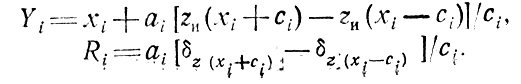
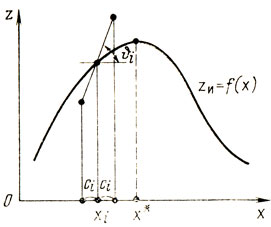
Puc. 7.2

Анализ случайной, составляющей: из выражения R_i и исходных предпосылок следует М [R_i] = 0, D [R_i] = 2(a_i/c_i)²D[δ_z], где D [δ_z] - дисперсия ошибки, не зависящая от i. Требование

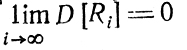
удовлетворяется при условии

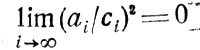
или

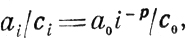
где а₀, с₀ - некоторые константы, p≥0,5; если p≥0,5, то

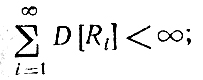
в случае необходимости можно требовать

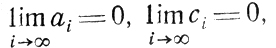
не нарушая рассматриваемых соотношений.

Анализ регулярной составляющей: обозначим разность z_и(x_i+c_i)-z_и(x_i-c_i) через (-Δz_иi); тогда Y_i = -x_i-a_iΔz_иi/c_i, следовательно,

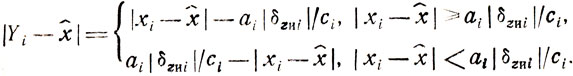(7.2)

Формула (7.2) не отличается по своей структуре от (7.1), поэтому все замечания, сделанные ранее применительно к (7.1) и касающиеся выполнения условия

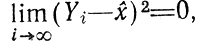
могут быть перенесены на (7.2) Так, положив

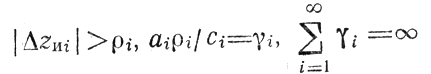
(в верхней строке 7.2) и

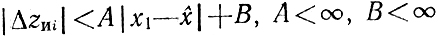
(в нижней строке 7.2), приходим к выводу о достаточности всего этого для обеспечения сходимости Y_i к х̂.

Закончив исследование условий сходимости конкретных методов стохастической аппроксимации, естественно поставить вопрос: в каком отношении находятся х и х^*? Очевидно, ответ может быть один: если все те сведения, которые нужны исследователю для доказательства сходимости, относятся действительно к х^*, то х̂ ≡ х^*; следовательно, начинать поиск рассматриваемыми методами имеет смысл тогда, когда об х^* уже что-то известно.