Глава седьмая. Стохастические процедуры оптимального выбора. Проблема накопления информации

7.1. Ошибки эксперимента. Учет влияния случайных факторов

Здесь будут изучены схемы поиска X^*, z^*, содержащие элемент случайности. Основными причинами, определяющими необходимость внесения случайности в действия исследователя, являются погрешности результатов экспериментов, а также отсутствие информации о свойствах поверхности отклика. Для простоты в первую очередь рассматриваются задачи, в которых целевая функция имеет скалярный аргумент.

Предположим, что эксперименты, проводимые в интересах решения одномерной задачи поиска (см. гл. 5), не дают точных значений z-любое из получаемых z содержит некоторую ошибку δ_z. Она является случайной и носит аддитивный характер (измеренная величина z представляется как сумма истинного, но неизвестного исследователю значения z_и и рассматриваемой ошибки: z = z_и+δ_z ).

Чтобы учесть присутствие δ_z, необходимо располагать теми или иными сведениями о ней, причем полнота этих сведений может меняться в широких пределах, начиная от законов совместного распределения ошибок в разных экспериментах и кончая моментными характеристиками (математическим ожиданием и дисперсией) величины δ_z при конкретном фиксированном х.

Пусть на интервале [0, 1] выбрана точка х и требуется получить оценку z_и=f(x) в условиях, когда известно лишь математическое ожидание М[δ_z] (подобная задача возникает при попытке реализовать здесь какую- либо из детерминированных процедур поиска). Можно стремиться достичь результата путем набора статистик, повторяя многократно эксперименты в х и используя получаемые значения z для вычисления среднего z̄, после чего легко найти z_и = z̄-М[δ_z]. Проведение этих операций связано с затратами средств и времени тем большими, чем выше требования к точности оценки z_и. Вопрос о том, можно ли избежать подобных затрат (или по крайней мере повысить их эффективность) решается на основе следующих рассуждений: если в данной точке х проведены N экспериментов и определены z⁽¹⁾, z⁽²⁾ , ... , z^(N), образующие статистику, то допустимо считать

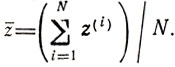
Если бы число экспериментов составило N-1, то оценка z̄ имела бы вид

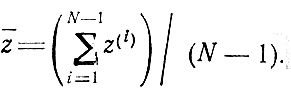
Сравнивая эти формулы, легко видеть, что между найденными z̄, обозначенными соответственно z̄_N и z̄_N-1 существует зависимость z̄_N = [(N-1)/N]z̄_N-1 + (1/N)z^(N) из которой следует:

- величина z^(N) являющаяся носителем "новой" информации, возникшей в последнем (по счету) эксперименте, входит в оценку z̄_N с весовым коэффициентом 1/N; убывающим с ростом N;

- величина Z̄_N-1 полученная на основе использования "старой" информации, содержащейся в z⁽¹⁾, z⁽²⁾ ... z^(N-1) входит в z̄_N с весовым коэффициентом (N-1)/N (он становится практически равным единице уже при N = 8-10);

- наибольшей информационной эффективности можно добиться, проводя в каждой точке х только один эксперимент (это означает отказ от попыток применения детерминированных процедур поиска х^*, z^* там, где есть ошибки эксперимента).

При решении оптимизационных задач исследователь обычно не интересуется более или менее точным "восстановлением" вида функции z = f (x). Он стремится построить правила выбора очередных х, основываясь на результатах предшествующих экспериментов, с тем чтобы в конце концов прийти к я^*. В условиях, когда есть ошибки 62, реализовать этот принцип можно путем такого выбора каждого нового значения х, при котором оно связывается определенной зависимостью с предыдущими х и соответствующими z(x). Вследствие этого в этом новом х будет учтена вся полезная информация (содержащаяся в предшествующих z) и вся ложная информация (обусловленная наличием δ_z), которая, однако, должна разрушаться по мере переходов от х_i к x_i+1 (i = 1, 2, . ..), если упомянутая выше зависимость между разными х выбрана надлежащим образом.

Пусть x_i+1 = W_i(x_i, z_i) или x_i+1 = W_i(x_i, z_иi + δ_zi). Очевидно, вид функции W_i должен влиять на характер сходимости последовательности значений x_i (i = 1, 2, ...) к некоторому пределу х̂ (в частности, к х^*). Если, например, W_i такова, что x_i+1 = W_1i(x_i, z_иi) + W_2i(δ_zi), то зная свойства δ_zi (или предполагая их), можно утверждать: при удачном выборе W_2i вероятность отклонения х_i+1 от х с увеличением i станет сколь угодно малой, а сам выбор преобразований W_1i, W_2i (с одновременным уточнением понятия сходимости x_i+1 к х̂ при i→∞) будет равносилен выбору стратегии поиска x^*, z^* в рассматриваемом случае. Таким образом, намечается путь решения задачи, для которого характерно то, что в каждой точке х проводится только один эксперимент, а фильтрация ошибок происходит за счет умелого сочетания длины шага и свойств случайных величин δ_zi. Эта идея лежит в основе методов стохастической аппроксимации.

Обратимся к определениям сходимости последовательностей случайных чисел (в дальнейшем они обозначаются большими буквами X, R и т. п., а их возможные значения - соответствующими малыми буквами).

Последовательность случайных величин X_i (i = 1, 2,...) сходится по вероятности к некоторому неслучайному пределу х̂, если для произвольного μ>0 вероятность события | X_i-x̂|≥μ стремится к нулю при i→∞, т. е.

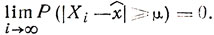
Последовательность случайных величин X_i(i = 1, 2,...) сходится в среднеквадратическом к неслучайному пределу х̂, если математическое ожидание квадрата модуля разности X_i-х̂ стремится

к нулю при i→∞, т.е.

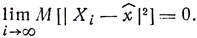
Последовательность {Х_i}, сходящаяся в среднеквадратическом, сходится и по вероятности (обратное положение места не имеет).

Пусть принята форма представления x_i+1 в виде суммы W_1i(X_i, z_иi) + W_2i (δ_zi). В силу случайности δ_zi величина W_1i будет случайной и может рассматриваться как случайная составляющая X_i+1; регулярной составляющей X_i+1 является W_1i. Вводя обозначения W_1i = Y_i, W_2i = R_i, получаем равенство X_i+1=Y_i+R_i, которое используется в последующем анализе как исходное.

Потребуем, чтобы последовательность случайных величин X_i+1 (i = 1, 2, ...) сходилась в средне-квадратическом смысле к некоторому пределу х̂. Формально это

требование выражается как

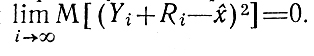
Математическое ожидание суммы, стоящей в квадратных скобках, есть (Y_i-x̂)²+2 (Y_i-x̂)M[R_i] + М[R²_i] или (Y_i-x̂)²+2 (Y_i-x̂) М [R_i] + М² [R_i] + D [R_i] (из общего определения дисперсии следует D[R_i] = М [{R_i -М[R_i]}²] = М[R²_i]-М²[R_i]). Для упрощения формул положим М[R_i] = 0, что позволит представить исследуемое условие в виде

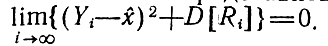
Здесь под знаком предела стоит сумма двух существенно положительных величин, и достаточно рассмотреть совместно условия

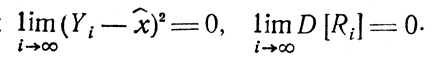
Обращаясь к первому из них, заметим, что функция должна Y_i быть построена так, чтобы одинаково хорошо управлять процессом поиска в двух случаях: а) точка x_i находится вблизи x̂, и есть опасность "перескочить" через х̂ при переходе к x_i+1; б) точка х_i находится настолько далеко от х̂, что нет оснований надеяться достичь х̂ за один шаг.

Для случая а) условие

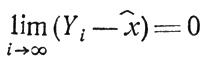
окажется выполненным, если потребовать, например, |Y_i - х̂|≤α_i, где α_i - член последовательности неотрицательных действительных чисел, обладающей свойством

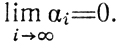
В случае б) этого требования недостаточно, поскольку желательно, чтобы каждый переход от x_i к x_i+1 (i = 1, 2, ...) сопровождался уменьшением расстояния до точки х. Здесь можно принять |Y_i-х̂|≤|x_i-x̂| - γ_i. Смысл этого неравенства заключается в следующем: регулярная составляющая величин X_i+1 (именно Y_i) должна отличаться от х̂ меньше, чем x_i, для чего вводится поправка γ_i (неотрицательное действительное число).

Чтобы процесс не остановился по прошествии некоторого конечного числа шагов, нужно иметь

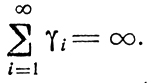
Рассмотренное условие сходимости процесса (точнее- его регулярной составляющей) может быть дано в обобщенном виде

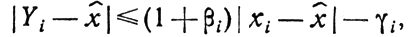
где

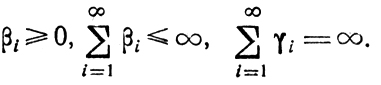
Эти замечания позволяют сделать важный вывод^*, чтобы доказать сходимость процесса (и в конечном счете решить задачу поиска х^*, z^*), необходимо располагать определенной информацией о свойствах функции f(x) = z_и. В дальнейшем при анализе процедур стохастической аппроксимации этот вывод будет конкретизирован.

Обратимся теперь к требованию

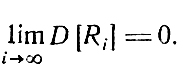
По мере совершения переходов от x_i к x_i+1 (i = 1, 2, ,..) характеристики ошибок δ_zi (например, их моменты) могут либо меняться, либо оставаться неизменными. В этой ситуации надежды удовлетворить рассматриваемому требованию связываются лишь с надлежащим выбором преобразования W_2i (δ_zi), выполняющего роль "фильтра" случайных помех δ_zi. Общим моментом здесь является необходимость соблюдения условия

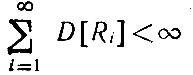
(в предположении независимости случайных величин δ_zi, i = 1, 2, ...).

Таким образом, процесс поиска в целом сводится к следующему: по мере проведения экспериментов,

в каждом из которых величина z = z_и + δ_z измеряется лишь один раз, регулярная составляющая Y_i очередного значения X_i+1 все меньше отличается от некоторого действительного числа х̂, а случайная составляющая Rt постепенно исключается сведением ее дисперсии к нулю.

Методы решения задач, основанные на этой идее, находят применение в различных областях исследований.