7.4. Стохастическая аппроксимация при оптимальных параметрах процесса. Роль гипотез

Определение оптимальных последовательностей корректирующих коэффициентов ставит самостоятельные задачи перед исследователем, поскольку соответствующие результаты во многом зависят от предполагаемых свойств функции z_и = f(х) и особенностей применяемой схемы поиска х^*.

Процедура Роббинса - Монро

Пусть известно, что z_и принадлежит классу линейных функций, т. е. z_и=Ax+B. Следовательно, истинное значение корня есть х^* = -В/А. Поскольку Y_i = x_i-a_iz_иi и σ²[R_i] = a²σ²[δ_z], выражение критерия принимает вид K_i = (a_i-1/A)²(Ax_i+B)²+a²_iσ[δ_z]^*. Стремясь достичь min K_i, будем выбирать а_i из условия dK_i/da_i = 2(a_i-1/А) (Ax_i + B)²+2a_iσ²[δ_z] = 0, что дает

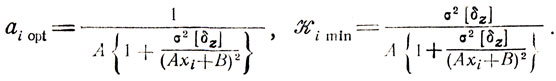(7.3)

Анализ формул (7.3) позволяет сделать следующие выводы:

- каким бы ни был уровень помех при данном i, знание класса функций, к которому принадлежит z_и = f(x), оказывается недостаточным; нужно по крайней мере знать А и быть уверенным в том, что отношение σ²[δ_z]/(Ax_i + B)² меняется с изменениями i должным (в смысле требований сходимости) образом;

- наилучший результат поиска (точное решение задачи) достигается при σ[δ_z] = 0 и a_iopt = 1/A = const; здесь K _imin = 0;

- наихудший результат поиска получается при σ[z_z]→∞; здесь первое же значение a_iopt обращается в нуль, и поиска как такового не будет, причем K_imin есть квадрат расстояния между х^* и исходной точкой x₁;

- при любой конечной дисперсии 0<σ²<∞ ответ на вопрос о величинах a_iopt и K_imin может быть дан лишь на основе каких-то дополнительных сведений о В.

^* (Индекс "i" в обозначении δ_z здесь опущен, чтобы не загромождать последующие формулы.)

Чтобы конкретизировать последнее замечание, обратимся к иллюстративному примеру. Ясно, что точное знание В сняло бы в целом задачу поиска, так как при известном А легко вычислить х^* = -В/А, поэтому будем считать B_min≤B≤B_max (величины B_min и В_max заданы), значение А известно и находится в пределах 0<A<∞, σ²[δ_z] = 1; требуется найти корректирующий коэффициент для точки x_i = - (В_max + B_min)/2A, полученной на предыдущем шаге (рис. 7.3). Без потери общности можно положить 1 = 1 и рассматривать x_i = x₁ как исходную точку поиска. В этих условиях Ax_i + B = B-В̄, где

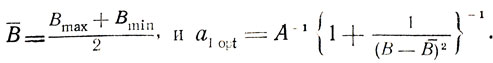
На рис. 7.4 представлен качественный график зависимости a_1opt от В. Вследствие неоднозначности В величина a_1opt определяется с точностью до 0≤a_1opt≤A^-1 × [ 1 + +4/(В_max-B_min)²]^-1, поэтому рис. 7.4 играет лишь вспомогательную роль (его роль возрастает с уменьшением неопределенности в оценке возможных В).

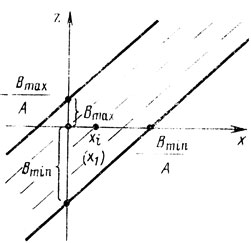
Рис. 7.3

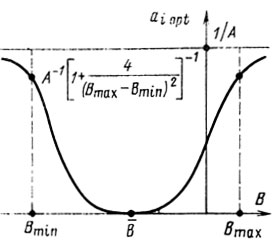
Рис. 7.4

Обратимся к выражению K_i, которое имеет здесь вид K₁ = (a_i-1/A)²(В-В̄)²+а²₁. Нетрудно заметить, при любом постоянном ai значение K_i. растет с увеличением модуля разности В-В̄ тем быстрее, чем больше коэффициент (a₁-1/A)². Это нежелательно из-за опасности получить большие в случае, если величина В окажется близкой к B_max или B_min. Наоборот, слабая зависимость K_i от В-В̄ при a₁≈1/A является в этом смысле более предпочтительной. Таким образом, в качестве "рабочего" значения a₁ выбираем a₁ = A^-1[1 + 4/(B_mах-B_min)²]^-1, что позволяет совершить переход в точку х₂. После того как координата х₂ будет вычислена, рассмотренная ситуация повторится снова с той лишь разницей, что при оценке а₂ придется учитывать требование сходимости процесса (это находит выражение в неравенстве a₂<a₁).

Предложенная схема решения не является универсальной; она возникает из конкретных условий задачи и может измениться с получением новой информации.

Процедура Кифера - Вольфовица

Пусть известен класс функций, к которому принадлежит z_и = f(х), причем f(x) дифференцируема по крайней мере дважды. Из уравнения df/dx=0 следует х^* = ξ(Р), где Р - совокупность параметров, определяющих конкретное значение f(x) при том или ином х (в схеме Роббинса - Монро в роли Р выступали А, В и ξ(Р) = -В/А).

Обозначим через ω разность z_и(x_i + c_i)-z_и(x_i-c_i), входящую в выражение Y_i так что х^*-Y_i = ξ(P)-x_i-a_iω_i/c_i. Критерий эффективности остается прежним:

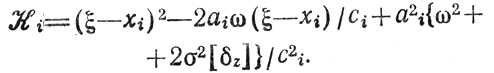
Чтобы найти оптимальные в смысле min K_i последовательности {а_i} и {с_i}, рассмотрим систему уравнений dK_i/a_i = 0, dK_i/dc_i = 0, которая в данном случае имеет вид

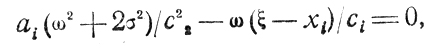(7.4)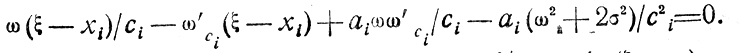

Складывая строки (7.4), получаем a_i^ωω'/c_i-ω'_ci(ξ-x_i) = 0, откуда следует либо а_iω/c_i - (ξ-x_i) = 0, либо ω'_ci = 0. Первое условие не может быть выполнено по

следующей причине: его подстановка в верхнее уравнение (7.4) приводит либо к ξ-х_i = 0, либо к σ² = 0, что противоречит смыслу задачи. Остается исследовать равенство ω'_ci = 0. Здесь возникают два предположения: существует единственное значение c_i = c_iopt, удовлетворяющее рассматриваемому равенству; свойства f(x) таковы, что не позволяют осуществить выбор c_iopt с использованием условия ω'_ci = 0. В первом случае нетрудно получить решение (7.4), дающее (после проверки достаточных условий существования K_i) искомый результат- c_iopt и

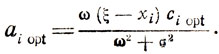
Во втором случае приходится выбирать c_iopt из каких- то дополнительных соображений, а для оценки a_iopt использовать только верхнюю строку (7.4), что, однако, не меняет результата. Таким образом,

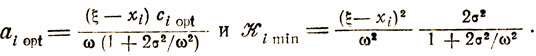(7.5)

Выводы, которые можно здесь сделать, не отличаются в принципе от тех, которые дал анализ формул (7.3):

- знание лишь класса функций z_и = f(x) оказывается недостаточным для определения оптимальной последовательности {а_i/c_i};

- точность получаемых решений тем выше, чем меньше σ²[δ_z], и наоборот; в предельных случаях (σ=0 и (σ=∞) соответственно K_i = 0, a_iopt=(ξ-x_i)c_ioptω^-1 и K_i=(ξ-x_i)²,a_iopt=0;

- при любой конечной дисперсии 0<σ²[δ_z]<∞ ответ на вопрос o величинах (a_i/c_i)_opt, K_min можно получить лишь на основе дополнительных исследований свойств функции z_и = f(x).

Все рассмотренные соотношения, относящиеся к процедурам стохастической аппроксимации, были даны в предположении М [R_i] = 0. Имеет смысл оценить, к чему приведет отказ от этого предположения. Требование сходимости процесса поиска в среднеквадратическом может быть представлено теперь как

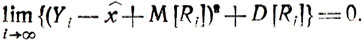(7.6)

Под знаком предела здесь стоит сумма двух существенно положительных величин, что равносильно замене (7.6) условиями

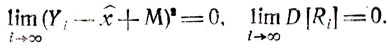
Ясно, что анализ сходимости, проведенный в 7.2, применим и к (7.6) (с заменой Y_i-x̂ на Y_i-x̂+М), хотя присутствие М[R_i] должно привести к появлению систематической ошибки в оценке х^*. Этот нежелательный эффект можно компенсировать внесением соответствующих поправок в гипотезы, касающиеся реальных характеристик z_и = f(x).

Методы стохастической аппроксимации, изученные в этой главе, допускают обобщение на задачи со многими переменными, где схемы переходов остаются теми же:

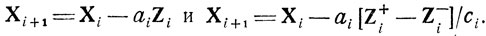
Ниже дан иллюстративный пример.

Пример: найти точку экстремума функции z_и = ^*f(x), если известно, что результаты экспериментов содержат случайные погрешности с характеристиками M[δ_z] = 0, σ²[δ_z] = 0,5 и f(x) = ax²+bx+c, а = 3/4, -10≤b≤5.

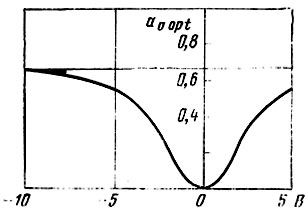
Рис. 7.5

Решение: поскольку на х не накладывается ограничений, можно использовать условие df/dx = 2ax+b = 0 для определения х^*, z^*; это приводит к задаче об отыскании корня функции z_и=Ax+B, причем А=1,5 и В∈[-10, 5]. Здесь целесообразно применить процедуру Роббинса - Монро с оценкой точности решений по критерию K_i (см. п. 7.4) .

а) Пусть в качестве исходной взята точка x₀ = 0 и z₀ = -4 (случайная величина); чтобы найти x₁ = x₀-a₀z₀, нужно определить

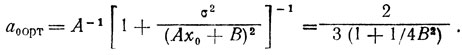
График зависимости а_{0 opt} от В приведен на рис. 7.5 (вследствие неоднозначности В он играет вспомогательную роль). Обращаясь к выражению K₀ = (а₀-1/А)²(Ах₀+В)²+а²₀σ² = (а₀-2/3)²В²+а²₀/4, замечаем, что наименьшее влияние величины В на K₀ достигается при а₀≈1/А приняв а₀ = 0,65, получаем x₁ = 2,6.

б) Пусть эксперимент, проведенный в точке x₁ = 2,6, дал z₁ = 1; следовательно,

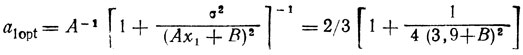
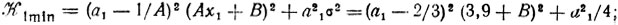
ситуаций повторяется: нужно выбирать ах близким к 1/A, сводя к минимуму зависимость K₁ от неопределенной величины В, поэтому полагаем a₁ = 0,6 (здесь учитывается требование a_i+1<a_i, см. п. 7.2) и x₂ = x₁-a₁z₁ = 2.

в) Пусть эксперимент в х₂ для z₂ = -0,5, т. е.

и a₂ принимается равным 0,55; отсюда х₃ = х₂-a₂z₂ = 2,28 и т. д.

Продолжение поиска по рассмотренной схеме (z_i выбирались с соблюдением условия σ²[δ_z] = 0,5) позволяет прийти к выводу, что истинное значение В вряд ли близко к -10 или 5; скорее всего оно находится в пределах -5, -1 (на это указывают выражения a_{i opt}, i = 0, 1, 2), и имеет смысл перейти к новой гипотезе: -5≤B≤3.

г) Пусть в качестве очередного x_i оставлено х₃ = 2,28 и z₃ = - 0,55; следовательно,

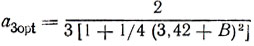
(принимается равным 0,5, см, рис. 7.6) и x₄ = = 2,55; очевидно, стандартные переходы с уменьшающимися a_{i opt} (i = 4, 5,...) можно продолжать до тех пор, пока не будут проведены все N экспериментов; последнее из имеющихся значений K_i определит конечную ошибку решения (в данном примере после 10 шагов получаем х^* = -2,4, K_min = 0,06).

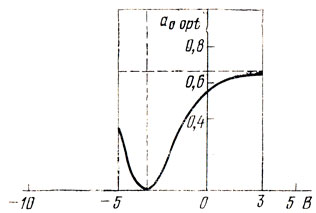
Рис. 7.6

В заключение заметим, что выбранная последовательность корректирующих коэффициентов a_i не является строго оптимальной; величина, на которую уменьшается a_i+1 по сравнению с а^*, сохранялась постоянной, равной примерно a₀/N≡1/(AN). Это правило удобно использовать тогда, когда исходная гипотеза о возможных В остается неизменной; в противном случае более перспективной оказывается "ступенчатая" последовательность {а_i}, в которой a_i сохраняются постоянными до очередной переоценки гипотезы, после чего назначается новое (уменьшенное) а_i и т. д.

Присутствие элемента случайности в действиях исследователя характерно и для методов случайного поиска, составляющих самостоятельную группу методов оптимизации.