7.5. Методы случайного поиска. Формирование обобщенных алгоритмов

Введение элемента случайности в схему поиска X^*, z^* может быть вызвано не только присутствием ошибок δ_z, но и недостаточной информированностью исследователя об особенностях поверхности отклика. Это обстоятельство приобретает решающее значение, когда f(X) является полимодальной функцией (со многими локальными экстремумами) и применение только детерминированных методов (например, градиентных) не приводит к получению X^*, z^*.

Таким образом, нет необходимости однозначно связывать проблемы случайного поиска с ошибками эксперимента; случайный поиск применим и тогда, когда ошибки есть, и тогда, когда их нет. Общая схема решения задачи сводится здесь к многократному последовательному повторению трех основных операций, уже упоминавшихся в предыдущих главах: операции сбора данных о свойствах z_и = f(X) в окрестности очередной опорной точки X_i (i = 1, 2, ...), операции перехода в новую опорную точку, совершаемого на основе собранных данных, а также информации, имевшейся до начала поиска или полученной на предыдущих шагах, и операции корректирования сведений об особенностях z_и = f(Х), совершаемой после того, как собраны новые данные (самообучение поисковой системы).

Эта схема не отличается в принципе от тех, что были рассмотрены в гл. 6; ее характерной чертой является предоставление исследователю права вводить случайности в процесс поиска. В качестве примера можно привести так называемый "слепой" поиск, идея и содержание которого заключаются в следующем: существуют некоторые представления о том, где в области Э может находиться X^* (пусть они выражены в принятом законе распределения X^*), и имеется начальная точка Х₀, в которой определено значение z=z₀; выбирается новая точка X₁ (случайным образом, в соответствии с характером распределения X^*), и найденная для нее величина z-z₁ сравнивается с z₀; если оказывается, что z₁ лучше z₀, то совершается переход в X₁ (в противном случае приходится повторять операцию выбора X₁); применительно к X₁ вся процедура повторяется, что позволяет найти Х₂ и т. д. Алгоритм "слепого" поиска может быть задан соотношениями

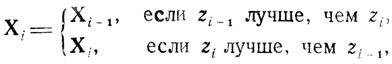
причем его эффективность будет тем выше, чем полнее учитываются изменения обстановки, возникающие после проведения экспериментов и выражающиеся в получении новых (апостериорных) распределений точки X^*.

Другой вариант схемы случайного поиска может быть связан с попыткой использования какого-либо детерминированного метода в сочетании со случайными изменениями начальных условий. Пусть организовано регулярное "перемещение" из исходной точки Х₀ в близлежащую точку Х° локального экстремума f(X) (например, по траектории наискорейшего спуска). После того как Х° будет достигнута, вводится случайное возмущение, переводящее процесс в новое состояние Xi, из которого нужно опять "двигаться" к новой точке Х° и т. д. В результате возникает разрывная траектория переходов в направлении X^*.

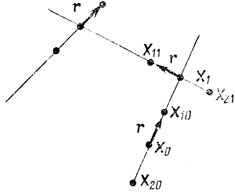
Рис. 7.7

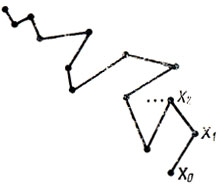
Рис. 7.8

Общие подходы к построению процедур случайного поиска, изложенные выше, находят свое выражение в конкретных методах решения оптимизационных задач.

Метод парных проб

Рассмотрим исходную точку Х₀ и единичный вектор r, связанный с ней (рис. 7.7); будем считать направление r случайным, распределенным, например, по закону равной вероятности.

Пусть X₁₀ и Х₂₀ - точки, заданные соотношениями Х₁₀ = Х₀+аr, Х₂₀ = Х₀-аr, где а - положительный параметр, определяющий расстояние от Х₀ до Х₁₀ и Х₂₀ вдоль r. Выбрав величину шага а_ш>0, можно предложить следующий алгоритм:

а) определяются значения z₁₀ = f(X₁₀), z₂₀ = ^*f(Х₂₀) и вводится функция

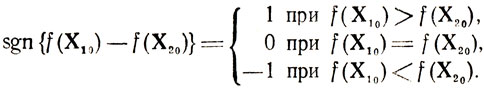
б) отыскивается точка X₁ = X₀+a_ш sgn[f (X₁₀)-f (X₂₀)], принимаемая за новую опорную точку;

в) совершается переход из Х₀ в X₁, после чего производится оценка первого апостериорного распределения вектора r; оно должно отличаться от равновероятного (принятого для Х₀);

г) в соответствии с новым распределением выбирается (случайным образом) направление r в X₁, определяются точки X₁₁ = X₁ + ar, X₂₁ = X₁-аr, и вся рассмотренная процедура повторяется; в результате формируется одна из возможных реализаций траектории случайного поиска, показанная условно на рис. 7.8.

Схема парных проб допускает различные модификации, многие из которых могут выступать как статистические аналоги известных детерминированных методов. Например, можно потребовать, чтобы направление r всегда совпадало с одним из координатных направлений, номер (j) которого есть случайная дискретная величина, распределенная в интервале [1, n] (аналог метода Гаусса-Зайделя). Точно так же, рассматривая направление r как градиентное, определяемое экспериментальным путем, легко построить (при случайном а_ш) аналог метода наискорейшего спуска и т. д. Подобные соображения могут лечь в основу синтеза обобщенных стохастических процедур поиска, объединяющих целые классы детерминированных методов и алгоритмов. Именно с этой точки зрения представляет интерес развитие теории случайного поиска, предлагающей методы исследования и оптимизации сложных много-параметрических систем.