8.3. Особенности задач составления расписаний. Теорема Джонсона

Разнообразие подходов к проблеме распределения времени вызывает необходимость уточнить понятия, относящиеся к конкретным задачам планирования (составления расписаний) и используемые при поиске их решений. Это поможет выявить и некоторые свойства изучаемых моделей.

Рассматриваемую проблему можно изучать либо в плане поиска наилучшего распределения времени и материальных ресурсов при выполнении заданного множества технологических операций, либо в плане поиска наилучшего распределения мест в очереди работ при известной и фиксированной их продолжительности. В первом случае возникают задачи нормирования (т. е. назначения обоснованных норм расходования ресурсов) и определения требуемых характеристик системы, во втором - задачи составления собственно расписаний (или просто задачи планирования работ).

Получение приемлемого расписания означает согласование многих действий и операций, направленных на достижение поставленной цели, что, в свою очередь, способствует совершенствованию программ деятельности производственных систем и развитию методов оперативного управления технологическими процессами.

Расписанием может быть назван документ, содержащий сведения:

а) о количестве и номенклатуре выполняемых работ, включая их этапы;

б) о моментах начала и окончания каждой работы, определяющих ее продолжительность;

в) о месте и технических средствах производства каждой работы;

г) о затратах времени (материальных ресурсов) на проведение всей совокупности работ.

Этих сведений достаточно для формального представления расписаний, и в дальнейшем они будут использоваться в решениях задач. На практике допустимы различные дополнения и уточнения данного определения, однако его основа сохраняется неизменной.

Многие понятия, относящиеся к изучаемым задачам, имеют неоднозначное терминологическое выражение, которое согласуется обычно с конкретной природой производственной системы. При построении формальных моделей нет необходимости применять специальные термины, хотя полезно еще раз обратить внимание на следующее:

- система представляет собой объединение производственных участков, выполняющих характерные функции и взаимодействующих в рамках исследуемого технологического процесса (см. рис. 8.2);

- участок представляет собой совокупность параллельно действующих технологических линий (исполнителей, каналов обслуживания и т. д.);

- работа есть совокупность операций (частных работ, этапов), выполняемых на соответствующих участках;

- допустимое расписание отождествляется с планом проведения работ, производственным планом, схемой загрузки участка и т. д.

Рис. 8.3.

Расписания могут быть заданы разными способами, среди которых наиболее наглядным является геометрический, основанный на использовании графика Гантта (или Гантт-карты). Каждой работе (или ее этапу) ставится в соответствие отрезок определенной длины, каждому каналу - прямая линия, вдоль которой размещаются попавшие на нее отрезки-операции. При известном начале отсчета времени взаимное расположение отрезков дает всю необходимую информацию. На рис. 8.3 в качестве примера показана схема распределения работ по каналам некоторого участка, оформленная в виде Гантт-карты; очевидно, та же схема может быть представлена как блочная матрица, элементами которой являются наборы чисел τ_υд, Δе_υ-1,l, t_υl. Иногда удобно строить вектор-функцию F(t) с компонентами F_l(t), получаемыми из условий: если в момент t≥0 линия с номером l простаивает, то F_l(t) = 0; если в тот же момент выполняется работа с номером υ, то F_l(t)=υ.

Для расписания, приведенного на рис. 8.3, F(t) = {F₁(t), F₂(t), . .., F₅(t)} при

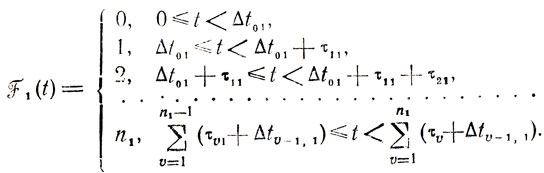
Простейшая задача теории расписаний формулируется следующим образом: имеются N работ и единственная технологическая линия, способная выполнить их в некоторой последовательности; известны и фиксированы затраты времени по каждой работе (τ_j, j = 1,..,N), и задан критерий эффективности (К). Требуется найти порядок проведения этих работ, доставляющий min К, при условии, что одновременно выполняется не более одной работы.

Поставленная задача может быть решена, в частности, методом полного перебора вариантов загрузки линии практически при любых ограничениях на выбор перестановок. Даже на примере этой задачи выявляются особенности, присущие вообще задачам составления расписаний:

- обычно приходится сталкиваться с так называемыми перестановочными расписаниями (комбинаторный характер задачи);

- число анализируемых вариантов решений, как правило, весьма велико, хотя в каких-то случаях оно может быть уменьшено за счет частичной упорядоченности работ, вводимой априори;

- ограничения задачи, оказывающие сильное влияние на получаемые результаты, должны исследоваться специально с целью унификации, классификации и т. п., что будет способствовать разработке методов решения, имеющих удовлетворительные характеристики сходимости;

- должны существовать разные способы задания К хотя бы потому, что некоторые из них делают задачу бессодержательной (например, если в простейшей задаче принять в качестве критерия полное время занятости линии N работами, то любая допустимая их перестановка, исключающая простои, даст min К); возникшая трудность устраняется здесь назначением штрафа за позднее начало работ.

Временной критерий широко используется на практике и относится к классу регулярных критериев; с ним связаны такие показатели, как суммарное время простоев оборудования, коэффициент загрузки технологических линий и т. и.

Наибольший интерес как в методологическом, так и в прикладном смысле представляет общая задача теории расписаний. Ее формулировка сводится к следующему: имеется производственная система, состоящая из M разнотипных L_к-канальных (k = 1, ...,M) участков (см. рис. 8.2) и N работ, каждая из которых будет выполняться в указанной системе и, следовательно, распадается на M этапов; заданы длительности проведения всех этапов каждой работы (матрица времен M×N) и условия-ограничения, определяющие специфику отношений между операциями в рамках рассматриваемого технологического процесса (приоритетность, необходимость ожиданий и т. п.). Требуется составить план проведения работ, минимизирующий полное время Т_с занятости системы (от момента начала первой до момента завершения последней работы).

Трудности решения общей задачи таковы, что точный оптимум не удается найти даже в случаях, когда нет ограничений, сравнительно невелико количество работ и т. д. Причины этого заключаются, по-видимому, в сложности структуры расписаний (дискретность, многовариантность), в отсутствии условий существования экстремума (приходится применять прямые методы его поиска), в несовершенстве оценок сходимости алгоритмов (часто исследователи ограничиваются просто набором статистик). Следствием этого является разнообразие подходов к проблеме и признание достаточности приближенных результатов во многих практических ситуациях.

Системы с расписанием являются обычно человеко- машинными системами, которыми нужно еще и управлять в ходе технологического процесса, поэтому вопрос о желательности точных и допустимости приближенных решений задач планирования должен обсуждаться в каждом случае специально. Возможности теории не всегда соответствуют запросам практики, что находит свое выражение в сложностях учета реальных ограничений, неоднозначности выбора функций штрафа и вообще в построении идеализированных моделей систем и процессов. В этих условиях следовало бы всегда признавать полезным результат, более или менее близкий к оптимальному и получаемый оперативно, однако оценка его точности требует разработки теории, дающей представление о свойствах собственно оптимума. Кроме того, развитие методов поиска экстремума способствует возникновению новых подходов к проблеме планирования и отысканию более компактных и обоснованных решений. В дальнейшем считаются равноценными результаты, дающие точный оптимум, и результаты приближенные, погрешность которых может быть оценена.

Возникновение теории расписаний связано с анализом частной задачи минимизации времени Т_с в системе, состоящей из двух одноканальных участков 2, L_1,2 = 1). Каждая из имеющихся N работ распадается, таким образом, на два этапа известной и фиксированной продолжительности τ_υ1, τ_υ2 (υ = 1,...,N). Вводятся предположения:

- очередность выполнения этапов сохраняется неизменной;

- на каждом участке одновременно проводится не более одной работы;

- работы выполняются без прерываний;

- последующий этап любой работы не может опережать ее предыдущего этапа.

Для названных условий С. Джонсоном предложена теорема (17), указывающая способ оптимального решения рассматриваемой задачи: при возможном произвольном выборе имеющихся N работ порядок их выполнения, доставляющий Минимум Т_с, должен быть таким, что работа υ предшествует работе υ+1, если

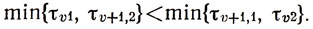
Значение теоремы Джонсона определяется ее наглядностью и простотой алгоритма упорядочения работ, к которому она приводит. Здесь имеет место довольно редкий случай, когда строго доказывается оптимальность предлагаемого расписания. Не останавливаясь подробно на доказательстве (его можно найти в [23]), полезно заметить, что оно представляет собой типичное исследование задачи о перестановочных расписаниях. Для конкретизации сделанных замечаний обратимся к примеру.

Пример: даны 5 двухэтапных работ (N = 5), выполняемых в системе с М=2, L_1,2 = 1; их характеристики сведены в табл. 8.1; требуется найти оптимальный (в смысле min T_c) порядок выполнения этих работ.

Таблица 8.1

Решение: построим новую таблицу данных, в которой перечислены все имеющиеся τ_υ1, τ_υ2 и указаны две последовательности работ, полученные сначала упорядочением чисел τ_υ1, а затем чисел τ_υ2 но признаку возрастания (табл. 8.2).

Таблица 8.2

С помощью табл. 8.2 удобно проверять выполнимость неравенств, устанавливаемых теоремой Джонсона для любых пар номеров υ, υ+1 проверка проводится последовательно в рамках ряда пред положений, рассматриваемых ниже.

1) Предположим, что работа II, попавшая в нулевой столбец табл. 8.2, занимает (965;+1)-ю позицию в будущей оптимальной расстановке работ (2≤965;+1≤N); это равносильно требованию min {τ_965;1, 2}< min {0, τ_965;2} или min {τ_965;1, 2}<0, где τ_965;1, τ_965;2 - параметры той работы, которая займет 965;-ю позицию. Очевидно, подобное неравенство невыполнимо (возможные значения τ_965;1 есть 2,5,6 и 8, см. среднюю строку табл. 8.2), и работа II не может идти ни за какой другой работой (она должна занять первое место и исключается из рассмотрения).

2) Предположим, что работа V, попавшая в первый столбец табл. 8.2, занимает v-ю позицию в будущей оптимальной последовательности, т. е. min {2, τ_965;+1,2} < min {τ_965;+1,1}. Среди возможных τ_965;+1,1 (средняя строка табл. 8.2) нет меньших единицы (работа II теперь не принимается во внимание), поэтому используемое неравенство сводится к min {2, τ_965;+1,2}>1 и оказывается невыполнимым, поскольку значения τ_965;+1,2 выбираются из {3, 4, 6} (см. нижнюю строку табл. 8.2). Следовательно, работа V может идти только за другими работами и должна занять последнее (пятое) место.

3) Предположим, что работа I, стоящая в очередном (третьем) столбце табл. 8.2, размещается на υ-й позиции. Из неравенства min {6, τ_965;+1,2}<min {τ_965;+1,1, 3} следует min {6, τ_965;+1,2}<3, что недопустимо из-за отсутствия τ_965;+1,2, меньших 4 (нижняя строка табл. 8.2); таким образом, работа I должна занять место после III и IV.

4) Предположим, что работа III (четвертый столбец табл. 8.2) попадает на и-ю позицию и min {5, τ_965;+1,2}<min {τ_965;+1,1, 4}; после проведенных проверок единственными значениями τ_965;+1,1 и τ_965;+1,2 остаются 8 и 6 соответственно; они нарушают рассматриваемое неравенство, поэтому работа III размещается после IV.

Анализ предположений на этом заканчивается (всего их здесь N-1). Результатом всех этих действий является последовательность работ {II, IV, III, I, V}, дающая наименьшую величину Т_с = 23. Полный перебор вариантов решений здесь исключается, так как всегда есть возможность ограничиться анализом не более N² пар чисел (τ_υ1, τ_υ2), (τ_965;+1,1, τ_965;+1,2).

Попытки распространить условия теоремы Джонсона на системы с произвольным количеством участков M>2) встречают серьезные трудности, обусловленные, в частности, необходимостью пересмотра требования не менять очередность выполнения этапов работ (оно было введено в рассмотренную выше задачу, поскольку при M≥2 допустимо сохранять порядок двух первых и двух последних этапов без потери общности результата).

Дополнительные сведения о свойствах задач составления расписаний могут быть получены при исследовании более сложных моделей оптимального планирования, в которых полнее отражены связи между отдельными операциями, производственными участками, способами организации работ.