8.4. Многоэтапный производственный процесс. Математическая модель упорядочения работ

Предположим, что некоторый технологический процесс сводится к последовательному проведению M разнотипных операций, каждая из которых выполняется на соответствующем оборудовании, входящем вместе с обслуживающим персоналом в состав какого-то одного производственного участка. Другими словами, на произвольно выбранном k-м участке (k = 1,...,M) проводятся только однородные операции (например, контроль данных, термообработка поверхностей и т. п.), а сам он характеризуется числом каналов L_k и их производительностью, зависящей сложным образом от технических показателей оборудования, принципов организации работ и т. д.

В момент t₀ в систему поступает заказ на выполнение N работ, причем каждая из них должна пройти через все M участков (т. е. является M-этапной). Предполагается, что любой этап любой работы не может быть повторен или выполнен с перерывами. Все технологические линии (в пределах того или иного участка) считаются равноценными в техническом отношении и одинаково пригодными к производству соответствующих операций. Критерием эффективности всей системы является полное время ее занятости указанными работами.

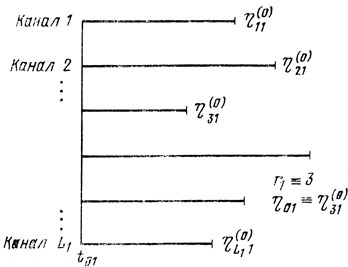
Рис. 8.4

Пусть в момент времени t₀₁≥t₀ принято решение начать работы по мере освобождения каналов первого участка. Ситуация, возникшая на этом участке к моменту t₀₁ такова, что все его каналы еще заняты, но известно, что первый канал освободится через время η⁰₁₁, второй -через время η⁽⁰⁾₂₁ и т. д. (рис. 8.4). Следовательно, реальное начало работ связано с моментом t₁₁=t₀₁+η₀₁, где

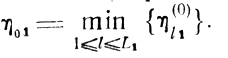
Если r₁ -номер канала, освободившегося первым, и τ₁₁ - продолжительность его занятия первой работой, с которой начинается рассматриваемый процесс, то

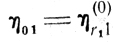
и момент подключения следующего канала есть t₂₁=t₁₁+η₁₁, где

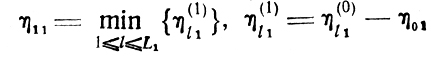
при

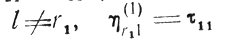
(рис. 8.5). Повторив подобные рассуждения применительно к t₃₁, t₄₁,...., получим общее выражение момента начала s-й по очереди работы (точнее, ее первого этапа) на участке 1:

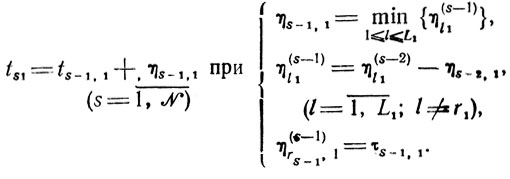
Момент окончания той же работы есть t̄_s1=t_s1+τ_s1 момент полного завершения операции 1 и время занятости участка 1 определяются как

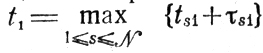
и T_i = t₁-t₁₁ соответственно.

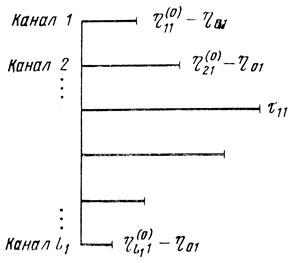
Рис. 8.5

Обратимся теперь к анализу операции 2. Принципиальная возможность начать' ее появляется тогда, когда на участке 1 будет завершена хотя бы одна работа (момент t₀₂). Ясно, что t₀₂ найдется из условия

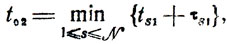
причем t₀₂>t₀₁. В общем случае реальное начало работ на участке 2 должно быть связано с моментом t₁₂ = t₀₂+η₀₂, где

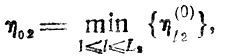
поскольку при t = t₂ каналы участка 2 могут оказаться занятыми (здесь возникает ситуация, подобная той, что имела место на участке 1 в момент t₀₁). Очевидно, выражение позволяет повторить для участка 2 все предыдущие оценки, однако необходимо иметь в виду следующее.

В момент очередного освобождения канала на участках 2, 3 и других могут оказаться незавершенными предшествующие этапы работ, и возникает опасность простоя канала; для учета этого обстоятельства в общие формулы введены величины Δt (см. ниже).

На каждом участке возникает своя нумерация работ вследствие того, что сохранять первоначальную очередность их выполнения, возникшую на участке 1, не имеет смысла из-за нежелательности дополнительных потерь времени (хотя в отдельных случаях сохранение очередности является исходным условием).

Учитывая сказанное, можно дать общие формулы для оценки основных моментов, отражающих ход технологического процесса.

- Номинальный момент начала работ на k-м участке

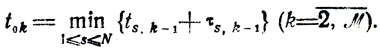(8.1)

- Момент начала s-й (по очереди) работы на k-м участке

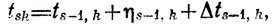(8.2)

где Δt_s-1,k≥0 - время возможного простоя канала (или вообще любая задержка t_sk относительно t_s-1,k+η_s-1,k);

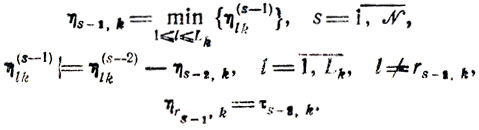
Момент окончания s-й работы на ft-м участке

(τ_sk - продолжительность работы).

Момент полного завершения k-й операции

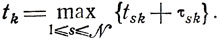(8.4)

- Полное время занятости k-го участка N работами

Среди приведенных формул особый интерес должна представлять формула для t_M - момента, когда закончится последняя операция и будет завершен технологический процесс. Зная t_M можно получить выражение критерия эффективности системы в виде

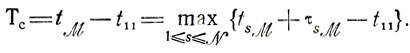
Таким образом, Т_с является довольно сложной функцией начальных условий η⁽⁰⁾_l1 влияние которых определяется присутствием в равенстве (8.6) величин t₁₁, t_sM.

количества каналов на каждом участке и их производительности, чисел M и N. Требование минимизации Т_с должно сопровождаться соблюдением целого ряда ограничений, налагаемых на переменные, входящие в (8.6). Считая число переменных равным n, число ограничений равным m и вводя для всех переменных единое обозначение х, приходим к следующей детерминированной задаче оптимального планирования:

- найти значения (x₁, х₂,..., х_n), доставляющие min_Xmax_sf(s, X) при условиях g_i(X)≤b_i, х_j≥0 (i = 1,...,m j = 1,..,n). Здесь X = (х₁, х₂,..., х_n), f(s, X) = t_kM+τ_sM-t₁₁, g_i(Х)- функции, входящие в ограничения.

Сюда же можно добавить (если это необходимо) требования целочисленности всех или части x_j.

Сформулированная оптимизационная задача относится к классу нелинейных задач математического программирования. Ее решение позволит определить расчетный оптимальный режим функционирования производственной системы, на который могут затем накладываться те или иные возмущения. Подобные задачи возникают при исследовании различных технологических процессов, причем основой всех различий являются ограничения g_i(X)≤b_i, отражающие в каждом конкретном случае специфику процесса.