Глава десятая. Методы оптимального распределения времени. Элементы машинного проектирования систем и процессов

10.1. Организация работ в многоканальной системе. Конечность алгоритма

Возможности практического применения и характеристики сходимости общего алгоритма (см. § 9.5) во многом определяются соответствующими показателями

частных алгоритмов, последовательная реализация которых должна приводить к получению желаемых значений Т_с. Рассматриваемые методы могут использоваться и самостоятельно в случаях, когда нет необходимости обращаться к усложненным схемам планирования. Соответствующие алгоритмы являются, таким образом, средством автоматизации проектирования производственных систем различной сложности и связанных с ними технологических процессов.

Исследуемая в этом разделе задача представляет интерес по трем причинам: она является типичной задачей теории расписаний, к ней сводится вся проблема организации работ при M = 1, методы ее решения оказываются применимыми и для поиска Т^*_С(И) (см. § 9.4).

Способ планирования, предлагаемый здесь, основан на использовании понятия диофантова уравнения Р(х₁, х₂, ..., х_n)=0, содержащего в левой части функцию полиномиального вида и решаемого только в целых (часто положительных) числах. Степень такого уравнения определяется степенью полинома Р(х₁, х₂,..., х_n).

В дальнейшем достаточно рассматривать только линейные уравнения вида

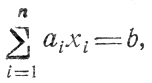
в которых b и a_i являются рациональными дробями. Приведя их к общему знаменателю, легко получить целочисленные b и а_i (например, для n = 3 соотношения

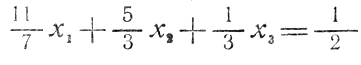
и 66x₁ + 70x₂ + 14x₃ = 21 эквивалентны).

Пусть имеются N работ, проводимых на участке, объединяющем L однотипных каналов. Каждый канал самостоятельно реализует все операции, предусмотренные технологией, поэтому любая работа может выполняться в любом канале, и время, необходимое для этого, известно. Требуется распределить N работ по L каналам так, чтобы полное время (Т) занятости участка этими работами было минимальным (предполагаем N>>L). На рис. 10.1 показан возможный вариант распределения работ. Здесь t₀ - общее начало отсчета времени, τ_υl - продолжительность выполнения υ-й (по порядку) работы в l-м канале (1≤υ≤n_i, 1≤l≤L); Δt_υ-1,l - задержка начала υ-й работы относительно окончания (υ-1)-й работы, Δt_0l - задержка начала забот в l-м канале относительно момента t₀. Очевидно,

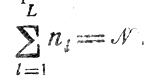
Время занятости канала с номером l(1≤l≤L) оценивается как

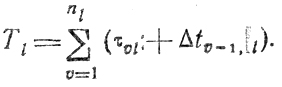
Оно отличается от среднего времени

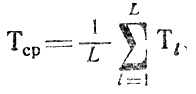
причем всегда

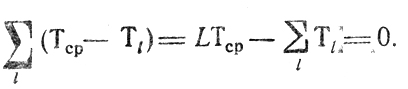
Следовательно, нельзя ожидать значений T, меньших T_cp, и задача заключается в том, чтобы минимизировать отклонения T_l(l=1,...,L) от Т_ср (наилучшим из всех было бы решение, дающее Т = Т_ср). В этих условиях увеличение Т_ср является нежелательным, но оно может произойти из-за неудачного выбора Δt_υ-1,l. Если Δt_υ-1,l фиксированы заранее (например, учтены потери времени на подготовку очередных работ или запланированы какие-то вспомогательные операции), то их удобно включить в соответствующие τ_υl, изъяв формально из рассмотрения. Если же Δt_υ-1,l выбираются произвольно, их лучше считать равными нулю с самого начала и не вводить в оценку Т_ср. Таким образом, в любом случае достаточно исследовать схему на рис. 10.2 с целью отыскания величины

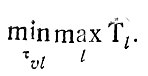
Здесь оказывается удобным использовать понятие линейного диофантова уравнения, возможности практического применения которого связаны с задачами об отыскании способов разбиения положительного числа А на слагаемые с известными свойствами или составления отрезка заданной длины из меньших отрезков и т. п. (в последнем случае требуется выбрать из имеющихся N отрезков с длинами τ_j (j = 1,...., N), такие, которые точно составят величину В. Формально это приводит к анализу уравнения

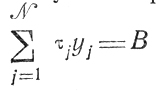
при условии, что переменные y_j могут принимать значения 0 или 1).

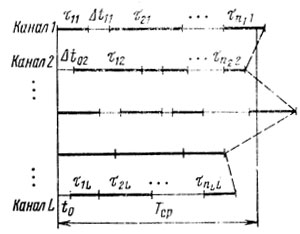
Рис. 10.1

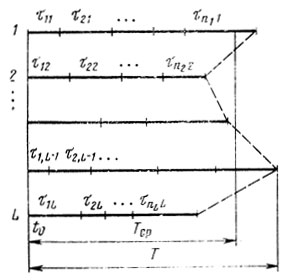
Рис. 10.2

Диофантовы уравнения (и тем более системы таких уравнений) разрешимы далеко не всегда, но для линейного случая условия существования решений сформулированы в общем виде.

Предположим, что из каких-то соображений выбраны Т_l>0 (l = 1,...,L). Можно ли указать вариант загрузки участка работами, отвечащий принятым Т_l? Ответ на вопрос будет утвердительным, если существуют неотрицательные решения системы диофантовых уравнений

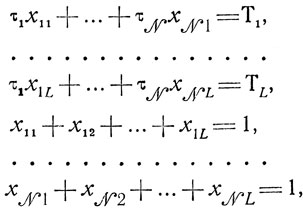(10.1)

где τ₁, τ₂, ...,τ_N - известные длительности выполнения работ (в произвольной нумерации). Каждое соотношение

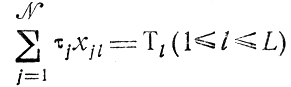
выражает требование точно составить из комбинаций "отрезков" τ_j величину Т_l (после чего вводятся обозначения τ_υl (рис. 10.2)). Ограничения на знак переменных х_jl (j = 1,...,N; l = 1,...,L) вместе с условиями

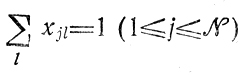
исключает возможность использования одного и того же τ для составления разных Т; (каждая работа выполняется только один раз в одном из L каналов), что равносильно требованию

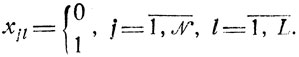
Основные трудности заключаются здесь в следующем:

- неясны принципы выбора величин T₁, Т₂, ..., Т_L;

- решения диофантовых уравнений довольно громоздки, и искать эти решения имеет смысл тогда, когда есть уверенность в их существовании.

Первая трудность может быть частично устранена, если иметь в виду, что наилучшей (в смысле минимума Т) комбинацией значений T₁, Т₂, ....,T_L является Т_l=Т_ср (l = 1,....,L) и ее нужно исследовать в первую очередь. Кроме того, всегда можно указать значения Т_l (l = 1,...,L), при которых система (10.1) разрешима, но которые почти наверное не доставляют минимума Т.

Для этого достаточно упорядочить τ_j по признаку не убывания, определить наименьший номер j=р, отвечающий условию

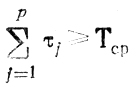
(рис. 10.3), сравнить между собой разности

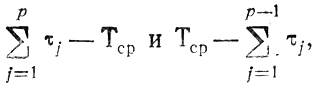
выбрать в качестве Т₁ либо величину

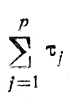
(если первая разность меньше второй), либо

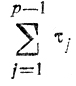
ту (если вторая разность меньше первой), исключив, таким образом, из дальнейшего рассмотрения τ_j, составившие T₁, и повторить всю эту несложную процедуру применительно к оставшимся τ_j, что даст сначала Т₂, затем Т₃ и т. д. Среди указанных T₁, Т₂, ... находится величина

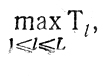
так что

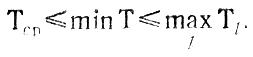
Если расхождение между Т_сp и найденным max_l T_l, окажется слишком большим, возникнет необходимость анализировать тысячи комбинаций Т₁, Т₂, ..., Т_L многие из которых будут затем отброшены как ненужные. Чтобы избежать этого, достаточно использовать следующий простой прием: фиксируется величина

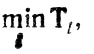
вычисляется разность

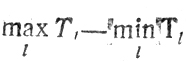
(на рис. 10.2 это было бы Т_L-1-T_L) и производится перераспределение работ между двумя каналами, позволяющее получить лучшее значение

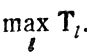
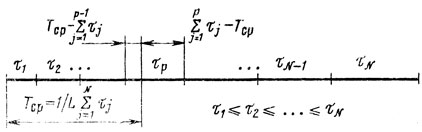
Рис. 10.3

Поскольку трудоемкость подобных операций невелика (они могут выполняться вручную даже при N>100 и легко формализуются), имеет смысл их повторять, добиваясь приемлемых отклонений

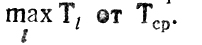
По смыслу исходной задачи все τ_j и Т_l есть рациональные числа. В формальном рассмотрении их можно считать целыми числами, меняющимися дискретно, причем такой же характер изменения должен иметь минимум Т. Это позволяет наметить пути перехода от одного (лучшего, но недостижимого) значения min Т к другому (сравнительно худшему) значению. Эти пути заключаются в последовательном анализе разрешимости диофантовых уравнений при тех Т_l, которые соответствуют принятому min Т.

Обратимся к теореме (20): диофантово уравнение

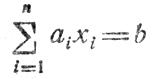
с целочисленными a_i и b имеет решения (положительные, отрицательные, нулевые), если наибольший общий делитель величин a_i(i = 1, ...,n) делит b.

Использовать это утверждение применительно к (10.1) можно лишь в негативном смысле (из-за жестких ограничений в выборе y_j, не учитываемых условиями теоремы). В результате станут известны Т₁, Т₂, ..., T_L, заведомо непригодные для включения в систему (10.1), а допустимые Т_l (l = 1,..., L) вместе с решениями уравнений будут определяться другими методами.

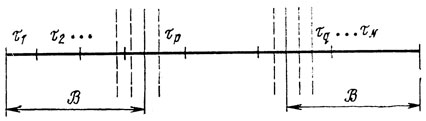
Рис. 10.4

Пусть дано простейшее уравнение τ₁y₁+τ₂y₂=B. Очевидно, его решения в виде комбинаций нулей и единиц существуют тогда, когда выполнено хотя бы одно из условий: τ₁ = B, τ₂ = B, τ₁+τ₂ = B. В общем случае (N переменных) число подобных условий составляет

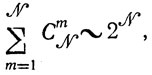
однако не все они представляют интерес.

Если упорядочить значения τ_j и найти соответственно наименьший и наибольший номера j = p, j = q, для которых

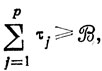
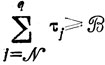
(рис. 10.4), то легко указать сочетания величин τ_о, подлежащие оценке (не имеет смысла рассматривать сочетания более чем из р-1 и менее чем из N-q+1 элементов, так как р самых коротких и N-q+1 самых длинных отрезков в сумме уже превысили B). Таким образом, количество сохраняемых условий уменьшается до

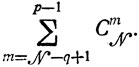
формирование связано с затратой значительных усилий, поэтому целесообразно ориентироваться сразу на все возможные значения B (вертикальные штриховые линии, рис. 10.4), классифицируя получаемые решения по признаку соответствия тем или иным B.

Если уравнение

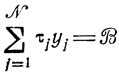
решено при допустимых B, то тем самым указаны наборы величин τ_j, дающих в сумме эти 38. Очевидно, план работы участка составляется только из "не пересекающихся" (т. е. не содержащих одинаковые τ_j) наборов, что позволяет ввести дополнительную классификацию найденных решений и затем организовать на этой основе поочередную проверку следующих гипотез: minT = Т_ср, min Т = Т_ср+НОД_τj, min T = Т_ср+2НОД_τj, ... (число гипотез определяется наилучшим

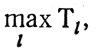
достигнутым при проведении подготовительных операций). В результате будет составлена оптимальная схема загрузки каналов.

В проведенном здесь исследовании отсутствовали какие-либо ограничения, и это было оправдано тем, что речь шла лишь о начальной задаче, в которой невозможно учесть все исходные условия. Исключение составляют требования приоритетного характера, вводимые на первых шагах решения и учитываемые путем повторения предложенной схемы планирования применительно к каждой приоритетной группе с последующей оценкой возможности уплотнения плана за счет левого сдвига работ в каналах.

Другим важным обстоятельством является необходимость значительных затрат времени на получение и проверку

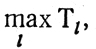
сочетаний величин τ_j однако все это приходится делать лишь тогда, когда ставится цель найти все варианты безусловно оптимального распределения работ на участке. Подобные ситуации встречаются редко, и их можно не рассматривать даже теоретически, поскольку всегда допустимо ограничиться приближенно оптимальными решениями, которые, требуя заметно меньших затрат, будут корректироваться на более поздних стадиях планирования. Кроме того, существуют приемы, позволяющие получать приемлемые результаты, перебирая порядка N² вариантов.

Алгоритм решения рассмотренной задачи объединяет 6 основных этапов поиска min T. К ним относятся:

- оценка Т_ср и определение наибольшего общего делителя чисел τ₁, τ₂, ...,τ_N- НОД_τj;

- составление предварительного плана сравнением разностей

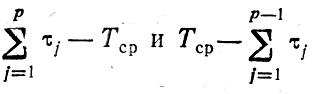
(см- рис. 10.3);

-уточнение предварительного плана путем перераспределения работ между двумя каналами и фиксация полученного

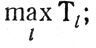
- определение нижней границы значений

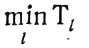
как

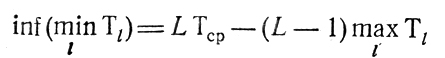
и выбор таких целых чисел В из диапазона

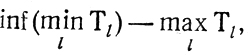
которые делятся без остатка на НОД_τj;

- решение диофантова уравнения

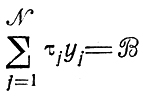
сразу для всех B с одновременной классификацией получаемых результатов;

- выбор гипотезы:

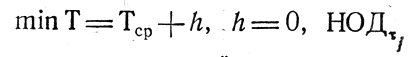
2НОД_τj,... и поиск соответствующих ей "не пересекающихся" наборов τ_j в зависимости от исхода поиска - конец процесса или переход к новой гипотезе.

Ниже дан пример применения предложенного метода.

Пример: четырехканальный производственный участок (L = 4) загружается семнадцатью работами (N = 17), продолжительность выполнения которых задана таблицей требуется найти оптимальный (в смысле min Т). вариант распределения работ на участке.

Решение: вычисляются

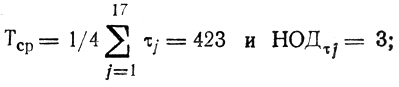
составляются

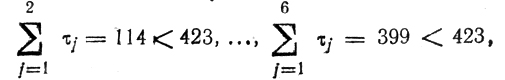
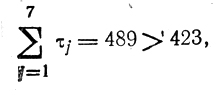
что дает р = 7; величина

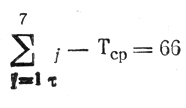
сравнивается с

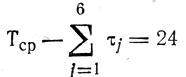
и фиксируется T₁ = 399 (в первый канал идут первые 6 работ);

- составляются суммы τ₇ + τ₈ = 180 < 423, τ₇ + τ₈ + τ₉ = 276 < 423,... из которых первой, превысившей T_cp, оказывается

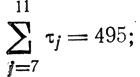
сравниваются

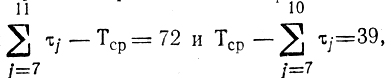
принимается Т₂ = 384 (во второй канал идут работы 7 - 10) и т. д.; в результате формируется следующий предварительный план загрузки участка:

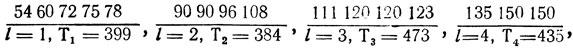
где

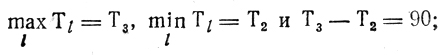
- производится перераспределение работ между вторым и третьим каналами с целью уменьшить T₃ (и соответственно увеличить Т₂) примерно на 0,5 (T₃-T₂) = 45 единиц, что приводит к передаче в третий канал работ 90, 96 (взамен 111, 120) и получению нового (улучшенного) плана (54 60 60 72 75 78), (90 108 111 120), (90 96 120 123), (135 150 150), в котором разность

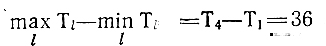
еще довольно велика; имеет смысл повторить операцию уточнения плана, передав в четвертый канал работы 60, 72 (взамен 150), и получить 54 60 75 78 150 90 108 111 120 90 96 120 123 60 72 135 150

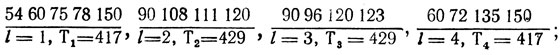
для значения

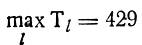
определяется

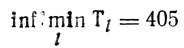
и исследуется набор чисел 405,406, ...,429; из них на НОД_τj = 3 делятся лишь 405, 408, 411, 414, 417, 420, 423, 426, 429 - возможные

- решается уравнение

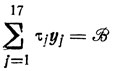
сразу для всех найденных

поскольку

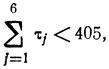
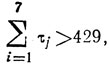
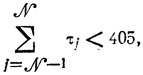
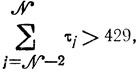
значения р. и q составят 7 и N-2, т. е. сочетания из 17 элементов по m должны рассматриваться при 3≤m≤6; их число есть ~22 000 и для их составления удобно использовать сводку сочетаний по 2 элемента; в результате заполняется таблица решений

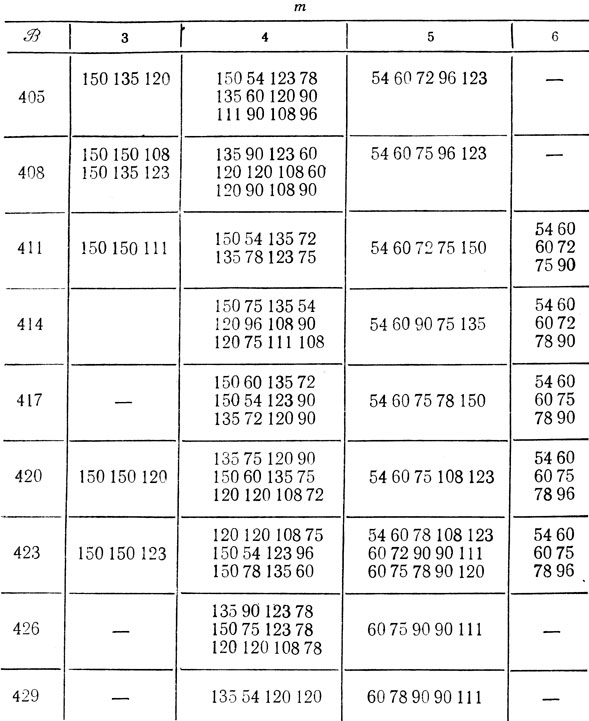
- принимается гипотеза: min Т = Т_ср = 423; в рамках этой гипотезы достаточно анализировать лишь одну (седьмую) строку таблицы решений;

"не пересекающиеся" наборы τ_j здесь - либо (60 72 90 90 111), (120 120 108 75), (150 54 123 96) (150 78 135 60), либо (60 75 78 90 120), (150 54 111 108), (135 72 120 96), (150 60 123 90); они представляют собой два (из возможных оптимальных) решения исходной задачи планирования работ на участке.

Дальнейшее накопление сочетаний τ_j привело бы к получению всех оптимальных решений, но это представляло бы чисто академический интерес.