10.2. Оценка нижней границы множества {Тс}. Вырожденные системы

Выше было замечено, что значения Т^*_с(и) могут быть получены из анализа задачи о распределении N работ с последействием по каналам производственного участка (см. § 9.4). В принципе эта задача мало отличается от только что рассмотренной в § 10.1, хотя и имеет свои особенности. Первой такой особенностью является требование выдержать определенный порядок выполнения работ в отдельно взятом канале (в задаче 10.1 этого не было, так как любая перестановка одних и тех же τ_j на l-й линии позволяла сохранять неизменным соответствующее T_l). Вторая особенность связана с необходимостью поиска . новой оценки наилучшего показателя общих затрат времени (вместо Т = Т_ср). Кроме того, можно ожидать усложнения процедур межканального обмена работами в ходе улучшений имеющихся промежуточных планов.

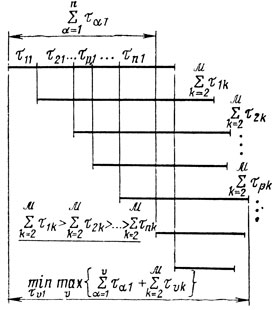
Рис. 10.5

Пусть дана технологическая линия, на которую приходятся n работ с последействием. Время выполнения υ-й по очереди работы есть

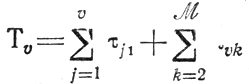
(рис. 10.5), а принятый порядок характеризуется величиной

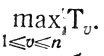
Всегда желательно разместить эти работы так, чтобы достичь

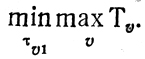
Это нетрудно сделать, используя утверждение приведенной ниже теоремы (21): для получения оптимальной в смысле

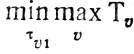
последовательности работ достаточно упорядочить величины

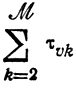
по признаку их убывания.

Доказательство: если рекомендуемая расстановка работ принята, то нетрудно указать номер р такой работы, что

Улучшение подобной ситуации связано с левым сдвигом р-й работы, происходящим за счет обмена местами с v-й работой (v<p) причем признаком допустимости обмена служит неравенство

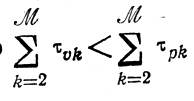
Действительно,

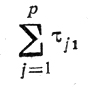
не изменится от такой перестановки, а сумма

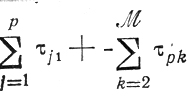
уменьшится только тогда, когда уменьшится слагаемое

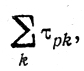
что и выражено в неравенстве). Но реализовать все это нельзя, так как по предположению

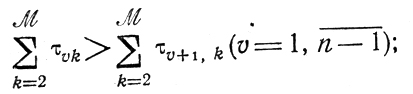
следовательно, | искомый минимакс достигнут. □

Если теперь снова обратиться к рассмотрению участка, объединяющего L линий, на каждой из которых работы упорядочены по признаку убывания

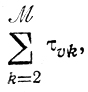
показателем его плана в целом становится величина

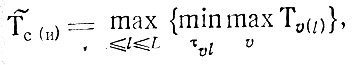
связанная с одним из номеров l.

В этой ситуации для любого l выполнено

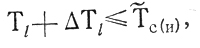
где

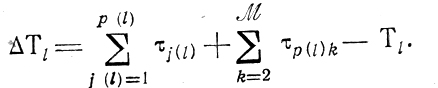
Очевидно

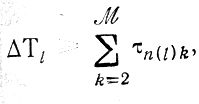
поэтому

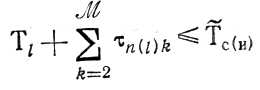
или (после суммирования по номерам д)

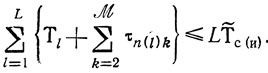(10.2)

Суммы

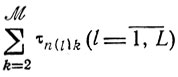
могут принимать значения, совпадающие с какими-то из N значений

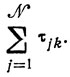
Обозначив r-е по величине число

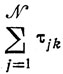
как

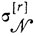
и имея в ввиду равенство

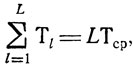
можно представить (10.2) в виде

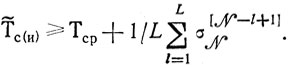
Таким образом, правая часть неравенства (10.3) показывает, какой предел улучшений Т̃_С(И) (и находящихся среди них Т^*_с(и)) достижим вообще (в § 10.1 это было просто Т_ср). В каждом отдельном случае идеальная оценка Т^*_С(И) будет скорее всего превышена, однако ни один план участка не даст Т^*_С(И), меньшее, чем

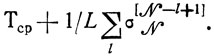
Последовательность действий, приводящих к получению Т^*_с(и), следующая:

- определяются

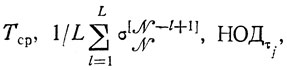
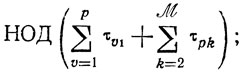
- составляется исходный план участка (По) по схеме, описанной в п. 10.1, и для него отыскиваются

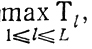
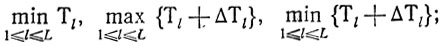
- проводится первое улучшение П₀ сначала с целью уменьшить

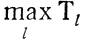
а затем

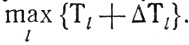
В результате возникают планы П₁ и П₂ с лучшими чем у П₀ показателями

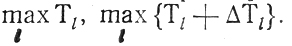
- планы Π₁, П₂ улучшаются по той же схеме; из четырех новых планов выбираются два, оставляемые для дальнейшей перестройки; признаками отбора служат те же

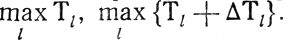
- рассмотренные процедуры повторяются до тех пор, пока не будет принято решение о переходе к анализу диофантовых уравнений с целью найти точный оптимум.

По-видимому, полностью выполнять всю эту программу нужно тогда, когда тенденции изменения max Т; и max {Т_l+ΔТ_l} совпадают (с улучшением первого показателя улучшается второй и наоборот). В противном

случае достаточно ограничиться только оценками Т_С(И). Дополнительные пояснения дает приводимый ниже пример.

Пример: четырехканальный производственный участок загружается работами с последействием (N = 21); их характеристики даны в таблице

Требуется найти оптимальный (в смысле Т^*_С(и)) план проведения указанных работ.

Решение. Вычисляются значения

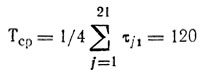
и

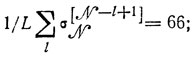
все НОД равны здесь единице; начальный план П₀ составляется по схеме, рассмотренной в § 10.1, т. е. производится суммирование упорядоченных τ_j1 до получения величины, превышающей Т_ср = 120 (здесь для этого достаточно взять первые 8 значений τ_j1). Накопленная сумма сравнивается с Т_ср, что позволяет разместить на первой линии работы (1)-(7). Повторение этой процедуры применительно к остальным работам приводит к искомому П₀:

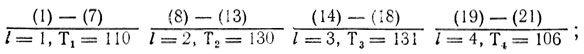
очевидными оценками являются

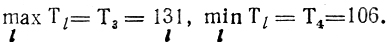
Вычисление

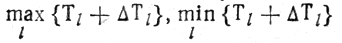
сводится к упорядочению работ в каналах по признаку убывания показателей ^MΣ_k=2 τ_jk и определению сумм

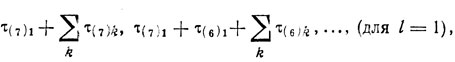
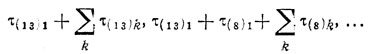
(для l = 2) и т. д. (рис. 10.6). Таким образом,

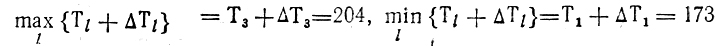
(расхождение оценок существенно).

Для улучшения Π₀ имеет смысл сразу ориентироваться на полученные предельные значения T_l+ΔT_l. работы (1) - (7) и (14) - (18), подлежащие перераспределению между каналами 1 и 3, упорядочиваются по признаку убывания

(7) (6) (14) (17) (18) (15) (2) (3) (4) (16) (1) (5). Какой бы ни оказалась будущая загрузка каналов 1 и 3, работа (7) обязательно займет первое место в одном из них (например, в том же канале 1), так как у нее наибольшая

Работу (6) передаем в канал 3, после чего реализуется следующая процедура:

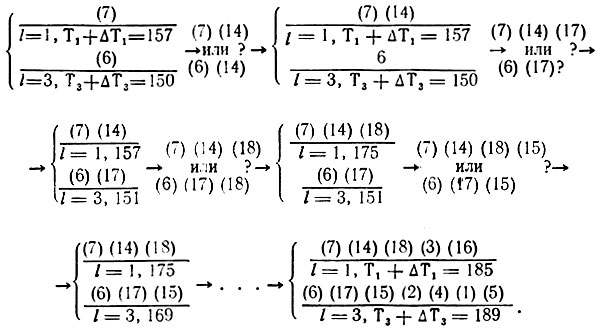
Теперь новый план (П₁) имеет вид

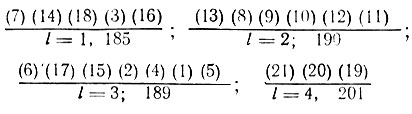
(улучшение П₀ произошло, но незначительное).

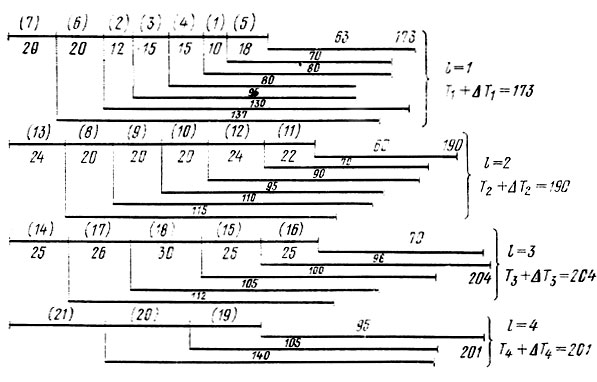
Рис. 10.6

-Корректирование П₁ связано с перераспределением группы работ, попавших в каналы 1, 4, т. е. (21) (7) (14) (20) (18) (19) (3) (16). Применяя схему, рассмотренную на предыдущем шаге, получаем

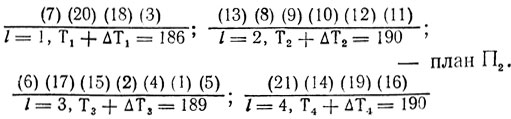
Произошло заметное улучшение П₁ (вместо

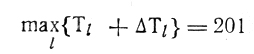
имеем 190); отклонение от идеального показателя

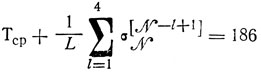
составляет ∼ 2%, и приходится решать вопрос о целесообразности преобразований П₂. В приведенном примере можно ограничиться достигнутым результатом, хотя дальнейший поиск мог бы привести к другому варианту загрузки линий:

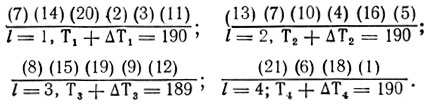
Вероятно, величина Т^*_с(и) = 186 либо недостижима, либо приближение к ней требует большого объема вычислений.