Приложение
Теорема существования неявных функций (к § 2.1)
Пусть дана точка
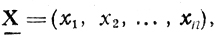
в которой выполнены условия
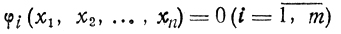
и
d(φ1,...,φm)/d(xk,...,xn) ≠ 0
Если
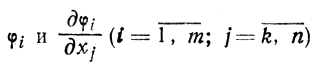
непрерывны в некоторой окрестности точки X, то т соотношений
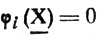
определяют хk, xk+1,...,xn как непрерывные функции от х1, х2, ... , xk-1. Если же рассматриваемый якобиан
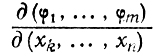
окажется равным нулю, то станет невозможным "однозначно определить xk,... , хn через х1, ... ... , хk-1.
Степени отношения 1/т (к § 5.3)

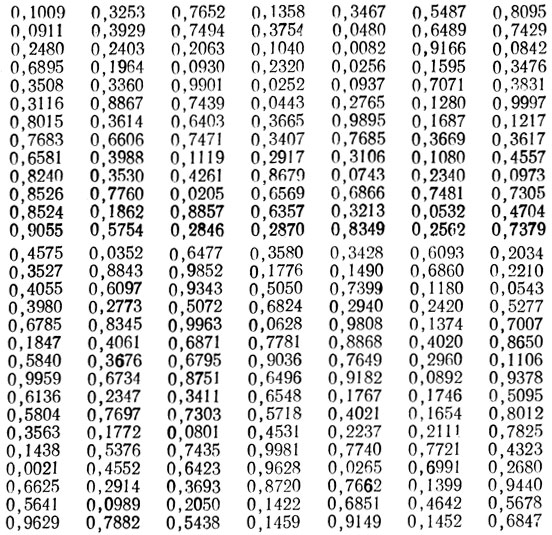
Случайные числа, равномерно распределенные в интервале [0, 1](к § 7.1, 7, А)
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'