10.7. Оперативное управление технологическими процессами. Практическое применение результатов теории

Одним из центральных аспектов комплексной проблемы организации обработки данных в АСУ (и производственных процессов вообще) является необходимость разработки методов оперативного управления, позволяющих устранять нежелательные отклонения процесса от намеченной схемы его развития. Соответствующие задачи могут быть решены с использованием результатов теории расписаний, получаемых для различных условий функционирования систем конвейерного типа.

Любая практическая ситуация характеризуется тем, что найденное в модели оптимальное распределение ресурсов (в частности, времени) нарушается периодически возникающими возмущениями (отказы оборудования, появление некачественного продукта, внеочередные работы и т. п.), последствия которых должны анализироваться с целью поиска наилучших управлений. Знание расчетных режимов оказывается полезным (и даже необходимым) потому, что их можно рассматривать как своеобразное начало отсчета, используемое и для фиксации отклонений, указанных выше, и для оценки результатов воздействий на систему, переводящих ее в допустимое (по условиям продолжения работ) состояние.

Чтобы формально описать ход производственного процесса (в том числе - процесса обработки данных), достаточно обратиться к векторам-функциям упоминавшимся в п. 8.3. Усложнение их структуры должно привести к удовлетворительному определению всех показателей исследуемого процесса в рамках принятой модели систем с расписанием (см. п. п. 8.2, 8.3).

Пусть дана система конвейерного типа, реализующая программу выполнения N, M-этапных работ в соответствии с планом, построеннным по рекомендациям гл. 9. В некоторый момент времени предпринята попытка оценить состояние производственного процесса путем получения ответов на следующие вопросы:

- какая работа (по порядку) выполняется в l-м канале k-го участка (l = 1,..., L_k; k = 1,..., М);

- сколько времени осталось (по плану) до ее окончания;

- какие дополнительные ресурсы используются в ходе этой работы? (здесь можно дать довольно полное описание динамики процесса, указав занимаемые объемы памяти ЭВМ, количества израсходованных реагентов, численность обслуживающего персонала и т. п. применительно к конкретной обстановке);

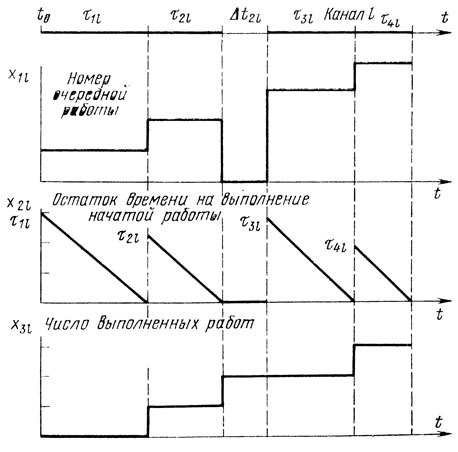
Рис. 10.13

- сколько работ еще предстоит выполнить (с учетом поступивших сверх первоначального задания)? и т. д.

Очевидно, искомые ответы представимы в виде наборов чисел x_jlk (j = 1, 2, ...), являющихся значениями соответствующих функций-компонент F(t), отнесенными к выбранному t. На рис. 10.13 приведен пример графического задания x_jlk(t) для произвольно взятого канала l одного из участков (индекс "k" опущен).

Сделанные замечания позволяют утверждать следующее:

-- функции x_jlk(t) являются разрывными, причем число точек разрыва конечно и имеют место только разрывы 1-го рода;

- параметрическое представление x_jlk = x_jlk(t) дает возможность построить фазовую траекторию "движения" исследуемой системы в ходе производства работ;

- полнота описания технологического процесса связана с количеством фазовых координат, учитываемых в модели, причем существует единый способ их формального выражения, не зависящий от природы процесса.

В последнем утверждении отражено важное обстоятельство: разрывные функции x_jlk(t) могут быть заданы как линейные комбинации вида

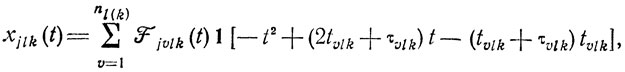(10.12)

где F_jvlk (t) - j-я характеристика операций, проводимых на k-м участке (функция времени); 1[ ]-единичная

ступенчатая функция; n_l(k) - число работ, выполняемых в l-м канале k-го участка; t_vlk, τ_vlk - момент начала и продолжительность v-й работы в канале lk.

Соотношения (10.12), определяющие поведение производственной системы в идеальных условиях, могут использоваться как для изучения ее внутренних свойств (устойчивости, управляемости), так и для решения задач синтеза оптимальных (по быстродействию или другому критерию) управлений.

Очевидно, операции управления должны заключаться не только в периодических пересчетах расписаний, но и в привлечении разнообразных активных средств воздействия на систему, изменяющих (в допустимых пределах) ход технологического процесса (ввод резервных линий, отказ от выполнения не срочных работ, пересмотр отдельных контрольных сроков и т. д.). Расширение возможностей управляющего звена в указанном смысле ставит самостоятельные задачи исследований в рамках теории кибернетических систем.

Идея специально организованного поэтапного формирования календарных планов для систем конвейерного типа, нашедшая свое выражение в рассмотренных подходах к проблеме составления расписаний, является перспективной с точки зрения применимости к разным классам задач проектирования производственных процессов. Области приложения методов теории расписаний могут быть самыми разнообразными, если говорить о содержательной стороне общей задачи (см. гл. 8), хотя на практике многое определяется соотношением между допустимым временем планирования и затратами времени на достижение заданной точности результата. Например, внутримашинная организация вычислительного процесса, проводимая непосредственно перед началом работ( и даже одновременно с ними), отличается по своему качеству (точности приближения к оптимуму) от того, что дает долгосрочное планирование в формально сходных условиях. Этим еще раз подтверждается необходимость разработки алгоритмов, допускающих сравнительно простую программную реализацию и обеспечивающих постепенное приближение промежуточных значений Т_с к предельному Т^*_с. Большую значимость приобретает также обобщение и формализация опыта, накапливаемого в ходе многократного расчета планов и позволяющего совершенствовать формы диалога между человеком-оператором и ЭВМ, что должно привести в конце концов к сохранению за оператором (и пользователем системы) лишь функции принятия высших решений.