§ 3.3. Практический способ нахождения выборки минимальных экстремальных взаимных расстояний между образами
Изложенный в § 3. 2 способ получения выборки экстремумов для случая многих классов может оказаться практически трудно реализуемым вследствие необходимости производить большие переборы как при составлении исходной выборки взаимных расстояний, так и при извлечении минимальных расстояний из групп.
С помощью габаритных эталонов можно существенно сократить указанные переборы, автоматически выделяя при этом ближайшие группы образов.
Использование габаритных эталонов позволяет в гистограмме взаимных расстояний всевозможных пар реализаций различных образов исключить из рассмотрения большие взаимные расстояния, вероятность которых стать экстремумами ничтожно мала.
Однако при формировании выборки экстремумов по сокращенной выборке взаимных расстояний (выделяемой габаритными эталонами) следует позаботиться о том, чтобы распределение номеров экстремумов было эквивалентно распределению минимальных номеров в группах при случайном разбиении полной выборки взаимных расстояний на N групп, как это было описано в § 3.2.
Для имитации случайности номеров порядковых статистик, образующих выборку экстремумов, можно использовать датчик равномерно распределенных целых чисел (от 1 до N).
Заметим, что распределение номеров полного вариационного ряда взаимных расстояний, которые оказались минимальными в N группах при случайном разбиении исходной выборки с хорошим приближением для достаточно больших N, можно заменить распределением минимальных номеров индексированных шаров в задаче размещения этих шаров по заданному числу ящиков (групп) до тех пор, пока все эти ящики не окажутся занятыми[3.4].
Можно дать еще другую интерпретацию имитации случайности номеров порядковых статистик в выборке экстремумов. N-гранная кость (N - число групп, или число экстремумов) бросается до тех пор, пока каждая грань не выпадет хотя бы один раз. При этом запоминается только тот номер бросания (номер порядковой статистики), когда каждая грань выпадает впервые.
Используя эти аналогии, можно сосчитать необходимое число nр бросаний М-гранной кости, чтобы с заданной вероятностью каждая грань выпала хотя бы один раз:
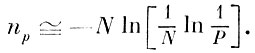
Это число с заданной вероятностью Р приближенно указывает нижнюю границу объема вариационного ряда исходных взаимных расстояний, который необходим для формирования выборки экстремумов объема N. Так, например, с вероятностью Р=0,95 для числа экстремумов N=100 необходимо рассматривать участок полного вариационного ряда взаимных расстояний до номера
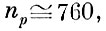
т. е. до 760-й порядковой статистики. Эта информация позволяет также определить минимальные размеры габаритных эталонов, которые обеспечивают необходимый перебор реализаций учебной выборки.
Запоминаемые номера бросаний, соответствующие первому выпаданию каждой из N граней кости, и есть номера членов усеченного габаритными эталонами вариационного ряда взаимных расстояний, которые образуют формируемую выборку экстремумов.
На основании приведенных соображений практический алгоритм получения выборки расстояний между ближайшими группами образов имеет следующую последовательность операций:
1) задать число N; число N - объем выборки экстремумов (или число групп) - выбирается из статистических соображений, указанных в § 3.2;
2) размещать датчиком случайных чисел последовательность номеров 1, 2, 3, . . . и т. д. по N группам до тех пор, пока в каждой группе окажется не меньше одного номера;
3) запомнить последовательность номеров, попадающих впервые в какую-либо группу, и упорядочить их по величине. Запомнить максимальный номер nmax; это тот номер, который впервые попал в последнюю незаполненную группу;
4) построить габаритные эталоны для каждого образа по учебной выборке и увеличить их на некоторое Δ1;
5) определить взаимные расстояния между "своими" и "чужими" реализациями образов, попавшими внутрь увеличенных габаритных эталонов, и упорядочить их по величине;
6) найти максимальное расстояние rmax, соответствующее запомненному в п. 3 nmax; rmax - максимальное расстояние в выборке минимальных расстояний объема птах. Если такого номера в упорядоченной выборке не оказалось, то увеличить габаритные эталоны на Δ1 и перейти к п. 5. Если такой номер нашелся, то перейти к следующему пункту;
7) увеличить габаритные эталоны на rmax - Δ1 и найти дополнительные взаимные расстояния между "своими" и "чужими" реализациями образов, попавшими внутрь увеличенных габаритных эталонов;
8) образовать окончательный вариационный ряд взаимных расстояний до номера nmax;
9) из вариационного ряда выделить взаимные расстояния, соответствующие запомненной последовательности номеров п. 3.
Эта выборка и рассматривается как выборка экстремумов.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'