§ 4.2. Создание системы признаков по аппроксимационному критерию

Способ нахождения линейных признаков по аппроксимационному критерию, излагаемый в настоящем параграфе, известен в литературе по распознаванию образов как разложение Карунена-Лоэва [4.1-4.3], в многомерном статистическом анализе - как метод главных компонент [4.4-4.6], в теории связи - как обобщенный спектральный анализ [4.7-4.9].

Необходимость включения описания этого метода вызвана тем, что излагаемые в следующих параграфах более эффективные методы создания признаков связаны с нахождением главных компонент.

По аппроксимационному критерию находится подпространство минимальной размерности, в котором реализации образов представляются с заданной среднеквадратичной ошибкой (базис этого подпространства и является искомой системой признаков).

Формально задача оптимизации признаков по этому критерию может быть сформулирована так:

Найти систему признаков {w_j}, минимизирующую функционал

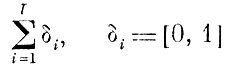(4.2.1)

при ограничении

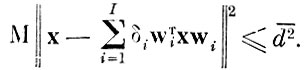
Система признаков {w_j}, удовлетворяющая (4. 2. 1), является совокупностью собственных векторов матрицы ковариации всей выборки, соответствующих J наибольшим собственным числам этой матрицы. При этом среднеквадратичная ошибка аппроксимации d̄₂, равная сумме (I-J) наименьших собственных чисел, определяет минимальное число признаков J.

Аппроксимационный критерий дает значительное упрощение описания, если исходные параметры сильно коррелированы. С помощью признаков, оптимизированных по этому критерию, удается достаточно точно в среднем описать реализации образов меньшим по сравнению с исходным описанием числом параметров.

Указанное разложение обладает рядом особенностей.

Первая особенность заключается в том, что члены этого разложения не коррелированы между собой (в смысле равенства нулю корреляционного момента всей выборки).

Вторая особенность разложения состоит в неравноправности его членов. Значимость каждого члена убывает с его номером и определяется соответствующим собственным числом.

При этом спектр матрицы ковариации (т. е. совокупность собственных чисел, являющихся дисперсиями по новым осям) распределен наиболее неравномерно. Наибольший среднеквадратичный вклад в аппроксимацию вносит первый член, второй - меньший вклад и т. д. Следовательно, вклад членов с высокими номерами будет весьма малым. Это свойство дает возможность при одном из способов дополнительной минимизации признаков отбрасывать признаки начиная с последнего.

Третья особенность разложения заключается в том, что величина ошибки аппроксимации не влияет на структуру самого разложения. Другими словами, изменение требований к величине ошибки не приводит к перерасчету членов разложения, а сводится лишь к добавлению или устранению нескольких последних членов разложения.