Приложение 4. VII. Алгоритм нахождения признаков по взвешенному одномерному дискриминантному критерию

Требуется найти систему признаков {β_j}, обеспечивающую разделимость центров тяжести в метрике с с порогом d₀ и реализацией - с порогом

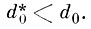
1. Выполнить пункт 1 приложения 4.III.

2. Выполнить пункт 2 приложения 4.IV.

3. Найти признак

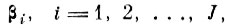
который является

собственным вектором взвешенной матрицы ковариации центров тяжести К_z, соответствующий максимальному собственному числу этой матрицы.

4. Для векторов z_qp, у которых

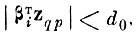(4.VII.1)

составим новую взвешенную матрицу ковариации.

5. Для нахождения признаков β₂, β₃, . . ., β_J выполнять пункты 3, 4 до тех пор, пока не останется векторов z_qp, удовлетворяющих условию 4. VII. 1 для хотя бы одного индекса i.

Для нахождения к дополнительных признаков по взвешенному одномерному дискриминантному критерию требуется к раз повторить процедуру приложения 4.V.

Каждый дополнительный признак

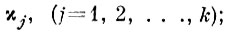
по взвешенному одномерному дискриминантному критерию требует проведения процедуры приложения 4.V, в которую необходимо внести небольшие изменения:

1) Формула (4. V. 6) заменяется на

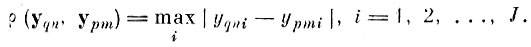(4.VII.2)

2) В пункте 5 приложения 4. V найти признак (первый дополнительный признак), являющийся собственным вектором матрицы ковариации К_z, соответствующий максимальному собственному числу этой матрицы;

3) в пункте 6 приложения 4. V добавить к признакам, найденным по центрам тяжести, один признак

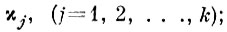
4) для нахождения последующих признаков χ₂, . . ., χ_k повторять процедуру до полного разделения реализаций с порогом d*₀ в метрике с.