Приложение 5. I. Формальное описание процедуры сокращения размерности исходного описания с использованием информации о признаках (первая задача)

1. Постановка задачи. Пусть X - I-мерное пространство исходного описания, a Ỹ - J-мерное подпространство признаков, оптимизированное по какому-либо из изложенных в главе IV критерию.

Обозначим также Y - полное I-мерное пространство признаков (преобразованное пространство исходного описания), первые J базисных векторов которого совпадают с базисом подпространства Ỹ, т. е. с признаками. Пусть х∈Х точка пространства исходного описания, а y и ỹ - отображения х в Y и Ỹ соответственно. Эти отображения осуществляются некоторым линейным оператором W^T (матрицей перехода), т. е.

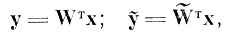
где

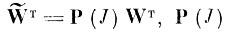
оператор проектирования на первые J осей. Индекс "т" означает операцию транспонирования.

Так как строки матрицы

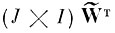
(или первые J строк W^T) являются признаками, то, следовательно, в этой матрице отражены все свойства используемого критерия.

Рассмотрим воздействие матрицы перехода в подпространство признаков на вектор

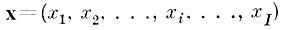
исходного описания

(5.I.1)

Для большей наглядности предположим (хотя это и не обязательно), что вектор х есть случайный вектор взаимных расстояний между реализациями различных образов в пространстве исходного описания. В силу свойств, описанных в главе IV, критериев, которые имеют в основном статистический характер, обычная или взвешенная дисперсия взаимных расстояний между классами после преобразования будет существенно перераспределена по новым осям - признакам. При этом первые J признаков

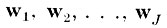
"берут на себя" наибольшую долю полной дисперсии взаимных расстояний. Доля дисперсии, приходящаяся на оставшиеся I-J новых осей, незначительна, следовательно, она мала и на каждую из них. Таким образом, преобразованный вектор

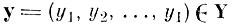
можно разбить на два подвектора

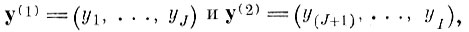
первый из которых определяет разделяющие в метрическом смысле свойства образов, а второй - песет лишь избыточную информацию.

Если величина критерия преобразованного вектора Y па последние I - J осей

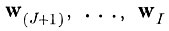
мала по сравнению с величиной критерия для полной системы признаков и не превышает некоторой величины θ², то это наводит на мысль о том, что в исходном описании имеются с точностью до θ линейно зависимые параметры относительно векторов взаимных расстояний между образами. Замена этих параметров линейными комбинациями оставшихся независимых, естественно, не может в силу малости θ² и непрерывности оператора W^T привести к значительному ухудшению разделимости образов в пространстве признаков. Отметим, что замена некоторых параметров исходного описания линейными комбинациями оставшихся эквивалентна их исключению, так как соответствующую замену можно было бы произвести в матрице перехода, а затем просто вычеркнуть θ - линейно зависимые параметры.

Произведем замену некоторых параметров, например, 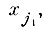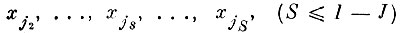- линейными комбинациями оставшихся

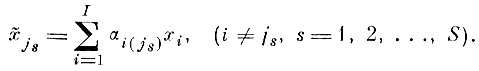(5.I.2)

Измененный вектор исходного описания имеет вид

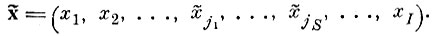
Преобразуем этот вектор в пространство признаков с помощью матрицы перехода W̃^T

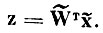(5.I.3)

Потребуем теперь, чтобы новый вектор z в некотором смысле не слишком сильно отличался от вектора ỹ, переведенного в пространство признаков по полному исходному описанию (5.1.1). Для этого образуем какую-либо выпуклую функцию модуля разности этих векторов

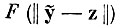
и будем искать ее минимум но совокупности векторов

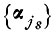
в среднем для всех реализаций учебной выборки и по всем наборам индексов {j_s} размера S:

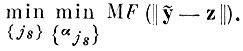(5.I.4)

Требуется найти максимальное число S исключаемых исходных параметров и указать каких именно, т. е. указать набор индексов

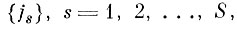
при которых функционал (5,1.4) не превышал бы некоторого заданного значения d.

Формально задача сокращения исходного описания с точки зрения наблюдателя, находящегося в подпространстве признаков, может быть записана следующим образом

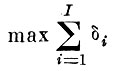
при условии

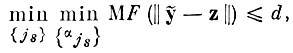
где

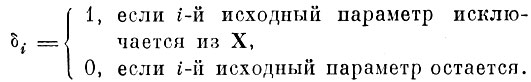
Очевидно, в такой постановке для больших I и S (а именно такие значения представляют интерес) эта задача практически нереализуема, так как минимум требуется искать, с одной стороны, по векторам

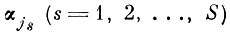
(это для данного набора индексов {j_s} поддается аналитическому решению), а с другой - требуется перебирать наборы индексов C^S_I раз, причем число исключаемых параметров S также переменно. Поэтому первым шагом к субоптимальному решению является отказ от поиска векторов

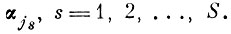
2. Субоптимальный алгоритм. В качестве коэффициентов линейных комбинаций (5.1.2) можно использовать элементы w_ij самой матрицы перехода W^T из X в Y.

В самом деле, если, как уже указывалось, последние координаты в (5.1. 1)

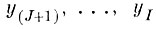
в среднем достаточно малы, то мы не совершим большой ошибки в силу непрерывности W^T, если "насильственно" сделаем некоторые из них

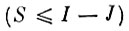
равными нулю. Тогда мы будем располагать S уравнениями связи, из которых можем выразить S исходных параметров как линейные комбинации оставшихся

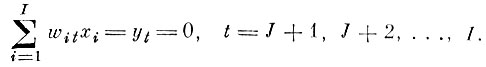
Пусть для простоты

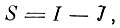
т. е. число заменяемых исходных параметров равно числу отбрасываемых в пространстве признаков не информативных осей. Тогда, если выбранная для замены комбинация исходных параметров есть

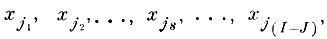
то любой из них может быть представлен в виде

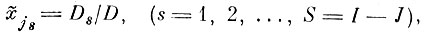(5.I.5)

где D - определитель, составленный из элементов матрицы перехода, которые соответствуют заменяемым исходным параметрам в уравнении (5. I. 3).

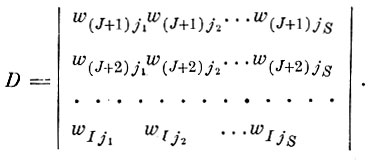(5.I.6)

D_s - определитель, полученный из определителя D заменой s-го столбца элементами c_t.

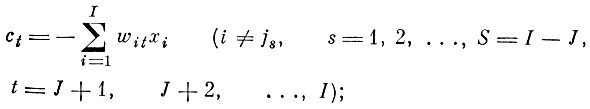
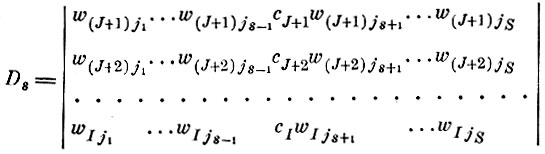(5.I.7)

Разлагая D_s no s-му столбцу, (5.1.5) можно записать n более удобном виде:

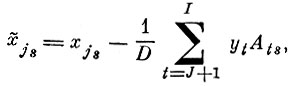(5.I.8)

где A_ts - алгебраическое дополнение D (5.1.6).

Линейные комбинации (5.1.8) подставляем в вектор исходного описания и переводим его в пространство признаков (5.1.3). Если теперь близость векторов ỹ и z определить как близость в среднем, то средний квадрат ошибки представления признаков с помощью сокращенного описания для данного набора индексов

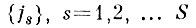
можно получить в виде:

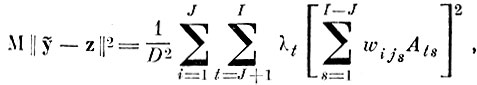(5.I.9)

или

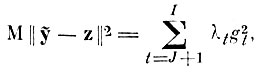(5.I.10)

где λ_t - дисперсия взаимных расстояний между образами на направление

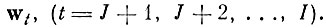
Можно требовать так же, как и при нахождении признаков, среднюю близость ỹ и z с весом, чтобы лучше учесть различие между "близкими" образами за счет несколько большей потери для различных "далеких". Введение весов не меняет существа самой процедуры. Необходимо лишь заменить дисперсии ^ на взвешенные дисперсии λ*_t.

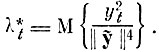
Как видно из (5.1. 9), перебор по подмножествам индексов {j_s}, s = 1, 2, . . ., S для нахождения минимума слишком велик, если число заменяемых параметров S исходного описания велико.

3. Упрощенный алгоритм. Дальнейшим шагом упрощения решения задачи является отказ от полного перебора вариантов, который заменяется последовательным перебором по одной переменной (по одному индексу j_s, s = 1, 2, . . .) некоторое число раз, до тех пор, пока величина ошибки (5. I. 10) не достигнет заданного порога.

На первом шаге ищется перебором такой исходный параметр x_js, замена которого линейными комбинациями оставшихся из некоторого t-го уравнения связи ("подвал" уравнения (5.1.1)) дает наименьшее расхождение между векторами ỹ и z (5.1.1)" (5.1.3).

Величина расхождения в этом случае определяется выражением

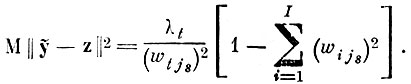(5.I.11)

Очевидно, что для определения минимума (5.1.11) следует в каждой строке "подвала" матрицы перехода W^T выбрать самый "жирный" по модулю элемент и просчитать (5.1.11) по всем возможным уравнениям связи (5.1.1).

На втором шаге процедура повторяется с учетом того, что один исходный параметр уже исключен, и т. д. После каждого шага величина (5.1. 11) сравнивается с порогом d̄² и после его достижения процедура обрывается.

Выбор самого "жирного" элемента в строке матрицы перехода удобно интерпретировать геометрически. Как уже указывалось, строки этой матрицы представляют собой векторы, заданные относительно арифметического базиса исходного описания, т. е. координаты этих векторов-признаков представляют собой косинусы углов с базисом описания. Наиболее "жирный" по модулю элемент строки есть наименьший угол между отбрасываемой (неинформативной) осью в пространстве признаков и каким-либо параметром исходного описания. Очевидно, что если отбросить эти параметры, то величина расхождения (5.1.11) будет наименьшая. Это несправедливо, к сожалению, для совокупности параметров, если матрица признаков не ортогональная.

Эти геометрические представления позволяют указать па самую простую процедуру минимизации описания (а соответственно, паи' менее оптимальную).

4. Простейший алгоритм. В каждом уравнении связи

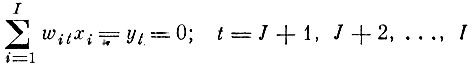
находится самый "жирный" по модулю элемент w_tjs. Эти элементы упорядочиваются по величине, и замена исходных параметров производится последовательно начиная с самого "жирного".

После каждого шага производится сравнение с порогом d, аналогично тому, как это описано в предыдущей субоптимальной процедуре, и т. д. Таким образом, необходимо совершить лишь однократный перебор. Такую процедуру можно применять тогда" когда размерность исходного описания во много раз превышает размерность пространства признаков.