§ 6.4. Использование преобразований сжатия для сокращения числа эталонов

В первой работе по методу эталонов [6.1] в качестве эталонов выбирались фигуры, имеющие одинаковые размеры по различным осям (гиперсферы, гиперкубы и т. д.). В большинстве случаев целесообразно произвести простейшие линейные преобразования над пространством признаков - преобразования сжатия, а построение эталонов образа вести уже в преобразованном пространстве. Такие преобразования не усложняют аппаратурной реализации эталонов и приводят к уменьшению их количества на образ, что можно видеть из сравнения рис. 6.2 и рис. 6.3.

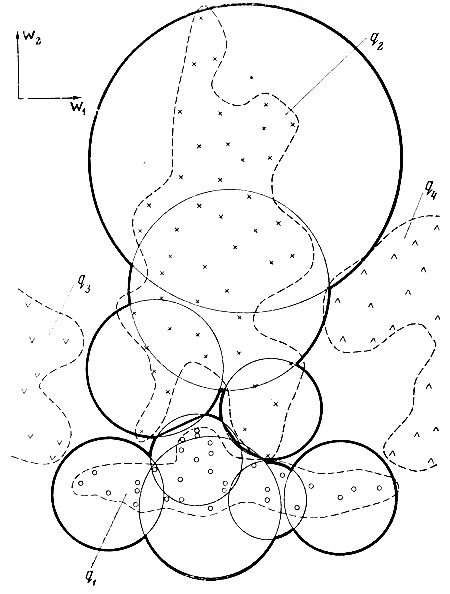
6.3. Эталоны, построенные в виде окружностей

На рис. 6.3 изображены те же образы, что и на рис. 6.2, но в качестве эталонов взяты не эллипсы, а окружности. Минимальное число эталонов в виде окружностей для образа q₁ в этом примере равно пяти, в то время как минимальное число эллипсоидальных эталонов равно трем.

Как видно из приведенных примеров, эффекта от замены сферических эталонов на эллипсоидальные следует ожидать тогда, когда разброс реализаций образа по разным осям различен. Так, в нашем примере разброс реализаций образа q₁ по оси w₁ превосходит разброс реализаций этого же образа по оси w₂, а отношение осей любого эталона для этого образа равно отношению указанных разбросов. Линейные сжатия пространства признаков к координатным осям, соответствующие разбросам по осям реализаций образа q₁, превращают эллипсы в окружности (см. рис. 6.4).

Подчеркнем, что число преобразований пространства признаков равно числу опознаваемых образов. На рис. 6.5 изображено пространство признаков, преобразованное в соответствии с разбросами реализаций образа q₂.

Построение эталонов в виде эллипсов можно рассматривать как последовательность трех операций: преобразование пространства в соответствии с разбросом реализаций образа по координатам; построение эталонов в виде сфер; обратное преобразование (при этом сферы превращаются в эллипсоиды).

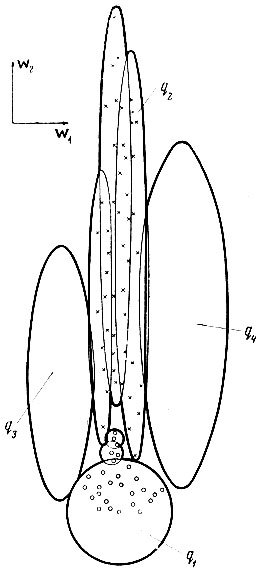
6.4. Учебная выборка в пространстве признаков, сжатом в направлении оси w₁

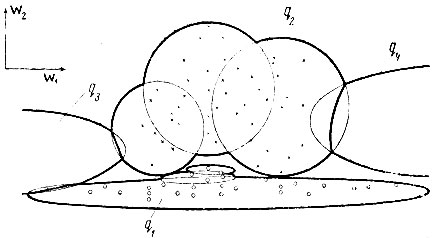
6.5. Учебная выборка в пространстве признаков, сжатом в направлении оси w₂