§ 6.7. Применение метода эталонов к частично пересекающимся образам

Детерминированный метод при построении решающего правила легко может быть распространен на случай, когда образы частично пересекаются, т. е. когда из-за недостаточности исходного описания или по другим причинам расстояния между небольшими частями выборок различных образов оказываются менее некоторой величины d, соизмеримой с аппаратурной погрешностью.

Отличие в процедуре построения решающего правила методом эталонов, вызванное тем, что образы частично пересекаются, заключается в следующем.

На первом шаге из учебной выборки исключаются те пары реализаций различных образов, расстояние между которыми меньше величины d.

На втором шаге для не пересекающейся части выборки по методике, изложенной в § 6.2-6.6, для каждого образа находится покрытие из минимального числа эталонов. При этом "радиус" эталона равен расстоянию от эталонной реализации до ближайшей реализации чужого образа, уменьшенного на величину аппаратурной погрешности (см. формулы 6.II.8а, 6.III. 3а).

После построения эталонных оболочек образов не пересекающиеся части учебной выборки будут опознаваться безошибочно.

Относительно реализаций учебной выборки, попавших в области пересечений эталонных оболочек различных образов, выдаются альтернативные или много-альтернативные ответы.

Таким образом, решающее правило, полученное на материале учебной выборки, состоит из минимального числа эталонов на образ. Эталоны для опознания не пересекающихся частей выборки и областей пересечения образуются с помощью операций математической логики.

Например, пусть пересекаются три эталона А₁, В₁, и C₁ относящиеся соответственно к трем образам q₁, q₂ и q₃. И пусть эталонные оболочки этих образов состоят из совокупностей эталонов

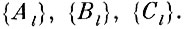
Тогда решающее правило для опознания не пересекающихся частей выборки образов имеет вид

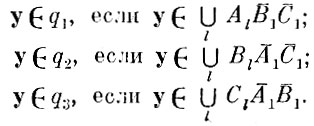
Для областей пересечения решающее правило имеет вид

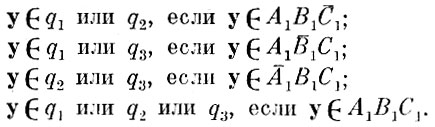
Алгоритм построения решающего правила для частично пересекающихся образов аналогичен алгоритмам приложения 6.II и 6.III. Ввиду того, что отличия в алгоритмах очевидны из текста параграфа, процедура построения решающего правила для частично пересекающихся образов в приложениях не приводится.