Приложение 6. III. Алгоритм построения эталонов в метрике с

Пусть в J-мерном пространстве признаков (метрика с) заданы учебные выборки классов q и q̄ и требуется найти эталоны для образа q.

Алгоритм сводится к следующему.

1. Вычисляется габаритный эталон, представляющий собой J-мерный параллелепипед для выборки q. Множество точек, покрываемых параллелепипедом с гранями, параллельными координатным осям, может быть записано в виде произведения его интервалов на координатных осях

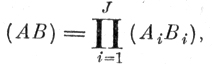
где (А_iВ_i) - интервалы на i-й координатной оси.

Интервалы на координатных осях (A_ΓiB_Γi), задающие габаритный эталон для класса q, в метрике с находятся по формуле

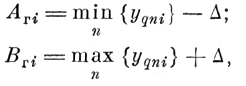(6.III.1)

где y_qni - значение i-й координаты n-й реализации образа q; Δ - число, учитывающее аппаратурную погрешность.

В дальнейшем под q̄ будем понимать множество только тех точек учебной выборки "чужого" класса, которые попадают в габаритный эталон класса q. Как отмечалось в § 6,6, такое допущение значительно уменьшает объем вычислений и при использовании метрики с но увеличивает число эталонов на образ.

2. Строится параллелепипед вокруг первой реализации образа q - точки y_q1.

а) Составляется столбцовая матрица ρ⁽¹⁾ расстояний от точки y_q1 до всех точек множества q̄. Элемент матрицы ρ⁽¹⁾_m определяется по формуле

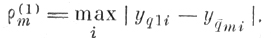(6.III.2)

б) Находится точка y_q̄s множества q̄, ближайшая к точке y_q1.

в) Определяется номер координатной оси который соответствует значению максимальной проекции вектора, соединяющего точку y_q1 и ближайшую к ней точку "чужого" класса y_q̄s,

г) Определяется порог по J-й координатной оси A_1j (B_1j).

При первом способе построения эталонной оболочки (см. § 6.2)

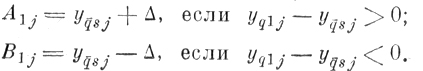(6.III.3а)

При втором-способе построения эталонной оболочки (см. § 6. 2)

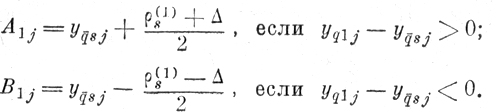(6.III.3б)

д) Отбрасываются из рассмотрения все точки класса q̄, для которых

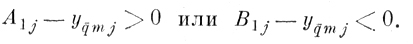(6.III.4)

е) Из матрицы расстояний ρ⁽¹⁾ вычеркиваются элементы, которые соответствуют точкам класса q, отброшенным по порогу A_1j(B_1j).

ж) Подпункты б, в, г, д, е повторяются до тех пор, пока в матрице расстояний ρ⁽¹⁾ не останется ни одного не вычеркнутого элемента.

При этом будет определена часть порогов, отсекающих все точки множества q̄ от точки y_q1 (в частном случае могут быть определены все пороги). Оставшимся порогам придают значения соответствующих порогов габаритного эталона.

Таким образом, определены все интервалы, задающие параллелепипед (А₁B₁), построенный вокруг точки y_q1

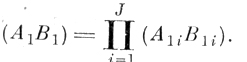(6.III.5)

Границы построенного параллелепипеда не зависят от номеров координатных осей и определяются только выбором реализации y_q1 и расположением точек "чужого" класса.

3. Аналогично пункту 2 строятся параллелепипеды вокруг каждой реализации образа q.

4. Определяются подмножества точек класса q, входящие в границы каждого из построенных параллелепипедов.

Подмножество точек q_m ⊂ q. которое входит в границы параллелепипедов (А_mВ_m), состоит из точек класса q, удовлетворяющих условию для точек

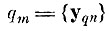(6.III.6)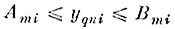

по всем i = 1, 2, ..., J.

Таким образом, получено разбиение множества точек выборки q на подмножества

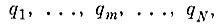
каждое из которых покрывается параллелепипедом соответственно

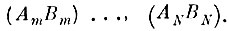
5. Составляется двоичная матрица принадлежности, для которой m-й номер строки матрицы соответствует номеру параллелепипеда; n-й номер столбца матрицы соответствует номеру n-й реализации класса q, точке y_qn

(6.III.7)

6. Для нахождения минимального числа эталонов двоичная матрица принадлежности φ минимизируется построчно при помощи поиска минимальных дизъюнктивных нормальных форм булевой алгебры.