Приложение 6. IV. Алгоритм минимизации числа признаков при использовании метрики с (первый подход)

Пусть в J-мерном пространстве признаков с базисом

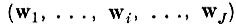
для образов q₁ ,. . ., q_l найдены эталоны в виде J-мерных параллелепипедов с гранями, параллельными координатным осям.

Требуется для m-го эталона образа q_l найти подпространство

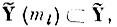
образованное минимальным числом базисных векторов пространства Ỹ, в котором бы в m-й эталон образа qt не попадало ни одной реализации образа q_l ("не q_l").

Как известно, множество точек, покрываемых J-мерным параллелепипедом с гранями, параллельными координатным осям, может быть представлено в виде произведения его интервалов на координатных осях

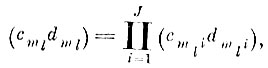(6.IV.1)

где

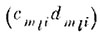
интервал m-го параллелепипеда образа q_l на i-й координатной оси.

1. Относительно m-го эталона образа q_l вычисляется двоичная матрица

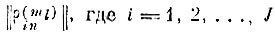
номер строки матрицы, соответствующий номеру координатной оси J-мерного пространства

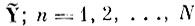
номер столбца матрицы, соответствующий номерам реализаций образа q̄_l; (m_l) - индекс, указывающий на то, что данная матрица выполнена для то-го эталона образа q_l.

Элемент матрицы

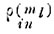
вычисляется по формуле

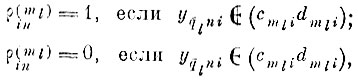(6.IV.2)

где

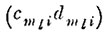
интервал m-го параллелепипеда образа q_l на i-й координатной оси; y_q̄Lni - значение i-й координаты n-й реализации образа q̄_l.

Для примера, приведенного на рис. 6-7, матрица

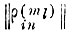
приведена в табл. 6. 1.

Для нахождения совокупности базисных векторов подпространства минимальной мерности

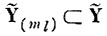
двоичная матрица

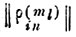
минимизируется построчно при помощи методов поиска дизъюнктивных нормальных форм булевых функций.

3. Аналогично находятся подпространства минимальной размерности для каждого из эталонов каждого образа.

4. Общее подпространство найденных признаков Ỹ* для всех эталонов всех образов определяется как результат суммирования всех подпространств, найденных для каждого из эталонов в отдельности

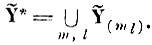(6.IV.3)