§ 7.4. Пример расчета параметров коррекции решающего правила

В этом параграфе для иллюстрации алгоритма статистической коррекции решающего правила производится полный последовательный численный расчет параметров коррекции для двумерной модели.

Выбор модели и расчет параметров коррекции производились в следующей последовательности.

1) В двумерном пространстве были заданы контуры границ пятидесяти ε-непересекающихся образов, которые, однако, линейно не разделимы. На рис. 3.2 показана часть пространства признаков, в которую вошли образы № 5 и 8.

2) Датчик случайных чисел генерировал учебные выборки образов, равномерно распределенные в этих контурах.

3) По учебной выборке (25 реализаций на каждый образ) были построены эталонные оболочки по двум вариантам (для сравнения) как в метрике с, так и в метрике l₂ (см. рис. 7.4 и 7.5).

В первом варианте в каждой точке строились эталоны в метрике с радиусом, равным половине расстояния до ближайшей чужой реализации, а затем "подравнивались" до размеров габаритных эталонов (см. рис. 7.4). Для 100%-ного опознания учебной выборки потребовалось в среднем но три эталона на образ.

Во втором варианте в каждой точке строился эталон в метрике l₂ радиусом, также равным половине расстояния до ближайшей чужой реализации (см. рис. 7.5). Затем были составлены двоичные матрицы принадлежности, которые минимизировались. В результате минимизации в среднем шесть эталонов на каждый образ безошибочно классифицировали учебную выборку. Из рис. 7.5 видно, что выборка не представительна, и минимальное покрытие недостаточно хорошо аппроксимирует истинные области образов.

4) Датчик случайных чисел генерировал контрольные выборки образов (по 25 реализаций на каждый образ).

По этим контрольным выборкам были получены две выборки {L_qn} и {l_qn} по 1000 "расстояний" для расчета предельных статистических характеристик L и I (см. § 7.3). Для этого каждая точка контрольной выборки y_qn сопоставлялась с двумя величинами:

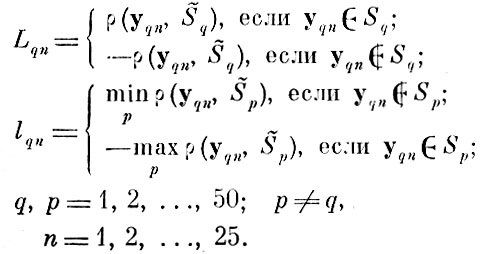
Расстояние измерялось в соответствующих метриках для двух вариантов.

5) По полученным выборкам {L_qn} и {l_qn} находились выборки экстремумов

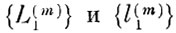
(см. главу III) по 10 экстремумов в каждой выборке (m = 1,2, . . ., 10).

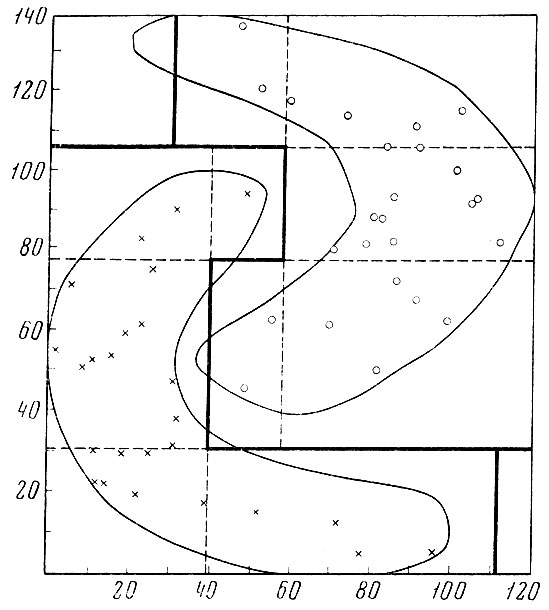
7.4. Эталонные области образов № 5 и 8, построенные по учебной выборке в метрике с

6) По методике, описанной в главе III, рассчитывались точечные оценки максимально возможного выброса реализаций за свою эталонную оболочку L̂ и максимально возможного проникновения реализаций внутрь эталонной оболочки чужих образов l̂.

Для этих предельных параметров строились также доверительные интервалы с доверительной вероятностью 0,95. Нижние границы этих интервалов использовались для коррекции решающего правила. Численные значения нижних границ L (α, N) и l(α, N) оказались равными L_c (0,95, 10) = 13 условных единиц в метрике с; l_с (0,95, 10) = 4,5; L_l2 (0,95, 10) = 8 условных единиц в метрике l₂; l_l2 (0,95, 10) = 1,5. Масштаб см. на рис. 7.4, 7.5.

7) Эталонные оболочки образов расширялись на величину L (α, N). При этом образовались области пересечения образов.

8) В области пересечения расширенных оболочек первоначальные эталонные оболочки сжимались на величину l (α, N). Сокращение области альтернативных ошибок происходило, если расширенные и сжатые оболочки продолжали давать пересечение. Окончательно выделенная область альтернативных ошибок показана на рис. 7.6, 7.7 штриховкой.

Коррекция решающего правила привела к значительному улучшению качества опознания образов.

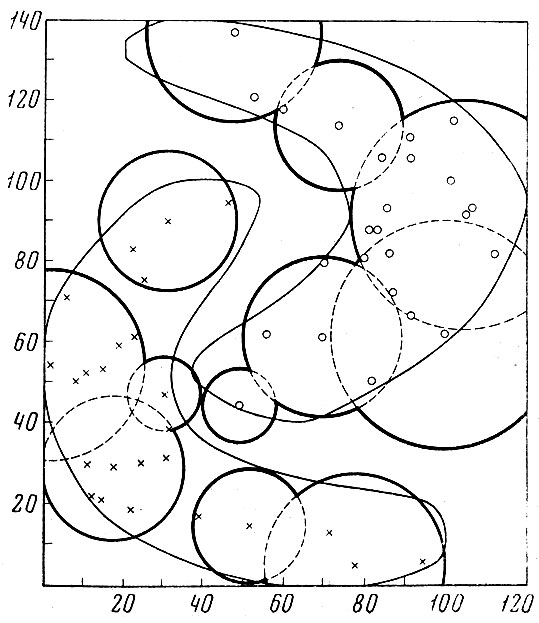
7.5. Эталонные области образов № 5 и 8, построенные по учебной выборке в метрике l₂

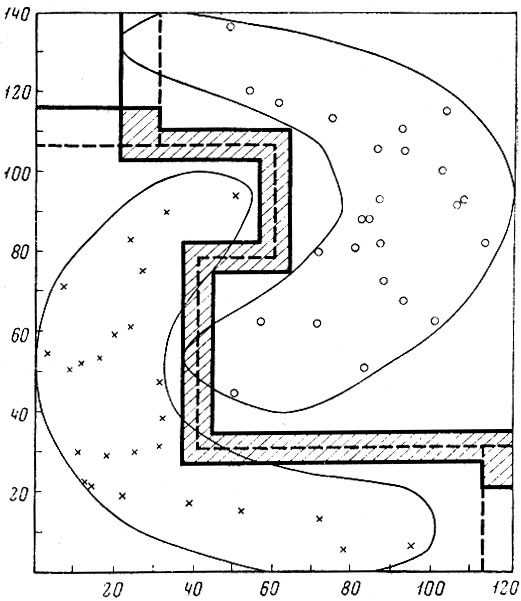
7.6. Решающее правило после процедуры коррекции для образов № 5 и 8 в метрике с (область альтернативных ошибок заштрихована)

В рассмотренном примере действительные величины ошибок разных типов легко подсчитываются как отношения соответствующих площадей, ограниченных заданными контурами и эталонными оболочками, в силу того, что распределения образов равномерны.

Решающее правило, построенное в метрике с, до проведения коррекции дало 4,2% ошибок неправильного опознания и 7,3% ошибок отказа в среднем по всем образам. Скорректированное решающее правило обеспечило отсутствие ошибок неправильного опознания, 1% ошибок отказа и 5,7% альтернативных ошибок (типа дилеммы). Напомним, что заданная величина ошибок неправильного опознания и ошибок отказа не должна была превышать 5% (β≤0,05).

Решающее правило, построенное в метрике l₂, до проведения процедуры коррекции дало в среднем по всем образам 12% ошибок отказа и 1,5% ошибок неправильного опознания. Скорректированное решающее правило обеспечило отсутствие ошибок неправильного опознания и ошибок отказа при 3,8% альтернативных ошибок (типа дилеммы).

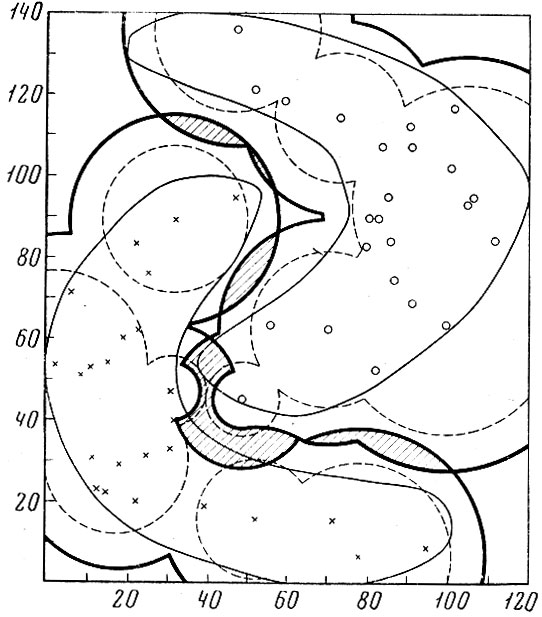
7.7. Решающее правило после процедуры коррекции для образов № 5 и 8 в метрике l₂ (область альтернативных ошибок заштрихована)