§ 8.2.5. Применение взвешенного дискминантного критерия

Алгоритм нахождения системы линейных признаков по взвешенному дискриминантному критерию (см. § 4.4) требует больших затрат машинного времени по сравнению с алгоритмом простого дискриминантного критерия только на этапе составления взвешенной матрицы ковариации. Вместе с тем этот критерий позволяет при переходе в пространство признаков сохранить разделяющие свойства исходного описания для наиболее близких пар образов. Заметим, что в этом критерии понятие "близость" между образами отождествляется только с близостью их центров тяжести, т. е. во взвешенном дискриминантном критерии теряется полная эквивалентность среднеквадратичного расстояния между реализациями различных образов средневадратичному расстоянию между их центрами тяжести, которая имела место в простом дикриминантном критерии. Сохранение же необходимого расстояния между отдельными реализациями достигается на следующем этапе при помощи модифицированного взвешенного дискриминантного критерия.

Для того, чтобы в пространстве признаков в первую очередь было обеспечено различие между "близкими" парами образов, в простой дискриминантный критерий вводится весовая функция, резко увеличивающаяся с уменьшением расстояния между образами.

По взвешенному дискриминантному критерию (4. 4. 1) находится система из минимального числа признаков, в которой при постоянной внутриклассовой дисперсии суммарная взвешенная дисперсия векторов, соединяющих центры тяжести образов, была бы не менее заданной величины.

В этом эксперименте и далее в § 8.3 и § 8.5 была использована весовая функция степенного вида

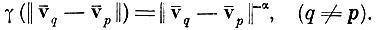(8.3.1)

Основанием для выбора показателя степени α послужили следующие соображения. Случай α=0 соответствует простому дискриминантному критерию, при котором наибольший вес при оптимизации системы признаков играют наиболее удаленные пары образов. Случай α=1 соответствует нормированию всех векторов взаимных расстояний, и, следовательно, каждый вектор учитывается с одним и тем же весом. Признаки, оптимизированные с такой весовой функцией, ориентированы на "пучки" векторов взаимных расстояний. Однако при выборе веса хотелось бы, чтобы в результате оптимизации признаки обеспечивали прежде всего разделимость близких пар образов. Случай α→∞ соответствует выбору признака, совпадающего по направлению с вектором самой близкой пары точек, т. е. признак становится детерминистским. Учитывая эти соображения, целесообразно выбрать показатель степени в интервале 1<α<∞. В экспериментах использовалась инверсная весовая функция с показателем степени α=2.

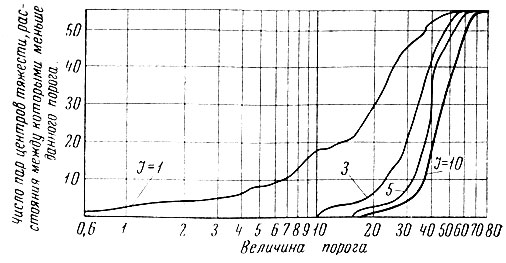
8.8. Гистограммы взаимных расстояний в метрике l₂ между центрами тяжести образов в 1, 3, 5 и 10-мерном подпространствах признаков, найденных по взвешенному дискриминантному критерию

На рис. 8.8 изображены зависимости числа пар образов, расстояние (в метрике l₂) между центрами тяжести которых меньше пороговой величины, от величины этого порога (гистограммы взаимных расстояний между центрами тяжести образов). Гистограммы получены для подпространств, образованных 1, 3, 5 и 10 признаками, найденными по взвешенному дискриминантному критерию. Из рисунка видно, что в отличие от простого дискриминантного критерия (см. рис. 8.7) наилучшее приближение получают векторы, соединяющие наиболее близкие пары центров тяжести.

В свою очередь векторы, соединяющие центры тяжести далеких пар образов, с увеличением размерности пространства признаков аппроксимируются хуже. Это указывает на то, что в пространстве признаков, найденных по взвешенному дискриминантному критерию, происходит выравнивание расстояний между центрами тяжести образов.

В таблице 8.5 представлены взаимные расстояния между центрами тяжести образов в пятимерном пространстве взвешенных дискриминантных признаков. Длины проекций векторов, соединяющих центры тяжести наиболее близких пар образов "два" и "ноль", "четыре" и "читаю", "один" и "три", мало уменьшились по сравнению с таблицей 8.3 и увеличились по сравнению с таблицей 8.4.

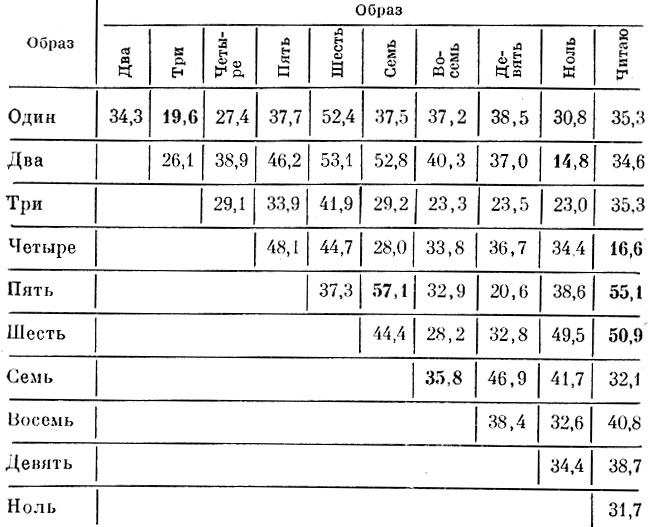
Таблица 8.5. Расстояния между центрами тяжести образов в метрике l₂ для 5-мерного подпространства признаков, найденных по взвешенному дискриминантному критерию

Зато расстояния между проекциями центров тяжести "далеких" образов уменьшились больше, чем при простом дискриминантном критерии.

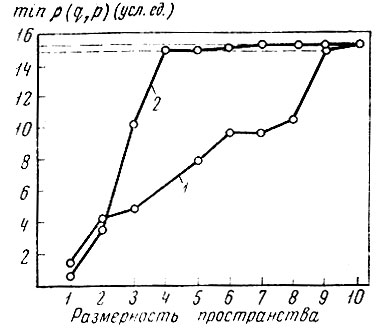
8.9. Зависимость минимального расстояния между центрами тяжести образов от размерности пространства признаков (1), найденных по простому и (2) взвешенному 2 дискриминантным критериям

Однако уменьшение расстояний между центрами тяжести далеких пар образов не ухудшает их разделимости. По абсолютной величине расстояния между центрами

тяжести далеких образов в пятимерном пространстве взвешенных дискриминантных признаков значительно превышают расстояния между близкими парами образов.

Очень наглядно иллюстрируют свойства простого и взвешенного дискриминантного критериев графики изменения минимального расстояния между центрами тяжести образов (в метрике l₂) в зависимости от увеличения размерности пространства признаков, найденного по простому дискриминантному критерию и по взвешенному дискриминантному критерию (рис. 8.9). По этим графикам видно, что для взвешенных дискриминантных признаков минимальное расстояние почти достигает своей полной величины уже при 4 признаках, в то время как для простых дискриминантных признаков та же точность аппроксимации достигается при 9 признаках. Заметим, что для достижения такой же точности требуется 17 признаков, найденных по аппроксимационному критерию.