§ 8.2.6. Применение модифицированного взвешенного дискриминантного критерия

Нахождение системы линейных признаков, гарантирующей разделимость в среднеквадратичном смысле для реализаций учебной выборки, производится в два этапа (см. § 4.5).

На первом этапе по взвешенному дискриминантному критерию для центров тяжести была найдена система из четырех признаков, которая обеспечила одномерную разделимость (в метрике с) с порогом d*₀=6, равным 44% от минимального расстояния между образами (см. табл. 8.1) для 99,77% пар реализаций различных образов.

На рис. 8.10 изображены зависимости числа не разделившихся с одномерным порогом d*₀=6 пар реализаций от количества признаков, найденных по взвешенному дискриминантному критерию для центров тяжести образов, и по взвешенному дискриминантному критерию - для неразделившейся части выборки. Для разделения небольшой оставшейся части реализаций с указанным одномерным порогом d*₀ пришлось бы дополнительно взять еще 15 признаков, найденных по взвешенному дискриминантному критерию для центров тяжести. Специально найденные по взвешенному дискриминантному критерию для неразделившейся части выборки дополнительные признаки позволили обойтись при разделении лишь 6 дополнительными признаками.

В таблицах 8.6 и 8.7 приведены минимальные расстояния между реализациями образов в 37-мерном пространстве исходного описания и в 10-мерном пространстве взвешенных дискриминантных признаков, образованном из четырех признаков, найденных по взвешенному дискриминантному критерию для центров тяжести и шести дополнительных признаков. Интересно отметить, что минимальное расстояние в метрике с между наиболее близкими образами "два" и "ноль" в 10-мерном пространстве взвешенных дискриминантных признаков по сравнению с исходным 37-мерным пространством увеличилось. В целом же для всех пар образов в 10-мерном пространстве признаков расстояния между реализациями различных образов в метрике с увеличились и остались равными по сравнению с расстояниями между реализациями образов в 37-мерном пространстве исходного описания для 36 нар образов из 55.

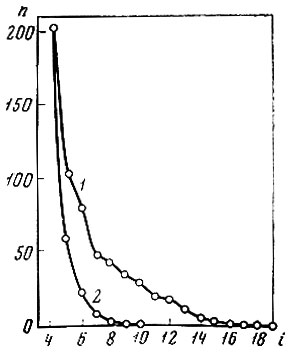
8.10. Зависимость числа не разделившихся пар реализаций n (с одномерным порогом d₀* = 6) от количества признаков: 1 - взвешенный дискриминантный критерий для центров тяжести; 2 - взвешенный дискриминантный критерий для оставшихся реализаций

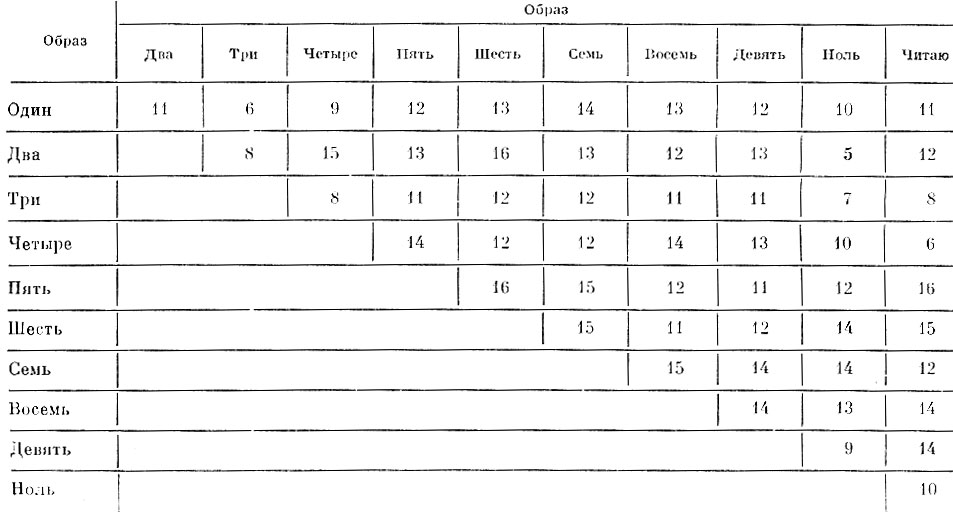
Таблица 8.6. Расстояния между реализациями образов в метрике с в 37-мерном пространстве исходного описания

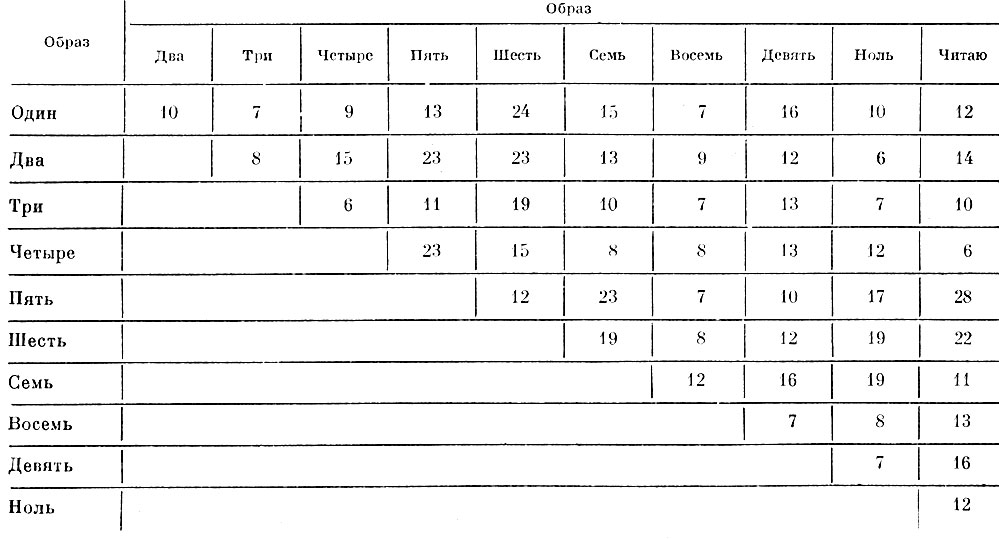
Таблица 8.7. Расстояния между реализациями образов в метрике с в 10-мерном пространстве взвешенных дискриминантных признаков

Следовательно, найденная система линейных признаков позволила не только сосредоточить разделительные свойства образов в пространстве меньшей размерности, но и для большинства пар образов улучшила их одномерные разделительные свойства.

Для более тонкой проверки разделяющих свойств пространства исходного описания и найденной системы признаков было применено самое простое решающее правило - габаритные эталоны в метрике с (см. главу VI). Очевидно, что разделяющие свойства эталонов по отношению к "чужим" образам тем лучше, чем больше размерность пространства. Однако увеличение размерности эталонов ухудшает их экстраполируемые свойства для реализаций "своих" образов.

В 37-мерном пространстве исходного описания в габаритные эталоны попало 28 реализаций "чужих" образов, что составляет в среднем на образ ошибку 0,7% (при заданной аппаратурной погрешности Δ, равной +7,5% от минимального расстояния между образами).

В пространстве взвешенных дискриминантных признаков при уменьшении размерности до 8 (почти в пять раз) ошибка разделимости (при той же аппаратурной погрешности) возросла до 47 (меньше, чем в 2 раза), что составляет в среднем на образ 1,2%. При уменьшении размерности пространства признаков до 6 (в шесть с лишним раз) ошибка разделимости увеличилась до 56 (в два раза).

Для проверки метрической близости образов в 10-мерном пространстве признаков, найденных по модифицированному взвешенному дискриминантному критерию, производилась попытка оценки параметра е по методике, изложенной в главе III.

Для этого с помощью габаритных эталонов, построенных в метрике с, выделялись ближайшие группы образов. "Близких" пар оказалось всего 27 из 55 возможных, а объем контрольной выборки для выделения экстремумов составил около 3000 слабозависимых взаимных расстояний между реализациями "близких" образов. Минимальное выборочное расстояние равно шести условным единицам (см. таблицу 8.7).

Точечная оценка метрической близости образов оказалась равной ε̂=4,1 условных единиц. Это говорит о том, что найденная система признаков сохраняет ε-непересекаемость образов.

Условный доверительный интервал при 5%-ном уровне значимости оказался широким

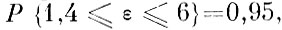
т. е. к полученной оценке ε со статистической точки зрения следует относиться с известной осторожностью, так как для выделения выборки экстремумов полученный объем контрольной выборки нельзя считать достаточно большим. Кроме того, дополнительные погрешности при оценке интервала возникают из-за недостаточного числа экстремумов (N=31).