§ 8.2.7. Применение одномерного детерминистского критерия

Одномерный детерминистский критерий (см. § 4.8) позволяет найти систему из минимального числа одномерно разделяющих признаков, обеспечивающих расстояние в метрике с для каждой пары реализаций различных образов не меньше некоторой величины d*.

В этом эксперименте был проверен только первый этап нахождения одномерных детерминистских признаков, в котором нахождение системы признаков осуществляется из условий одномерного разделения центров тяжести образов.

Минимальное расстояние между центрами тяжести образов в метрике с после осуществления нормирующего внутриклассовую дисперсию преобразования U^T равно 15,2 условным единицам (образы "два" и "ноль"). Поэтому порог d₀ был выбран соответственно равным 15 условным единицам. Следует заметить, что после нормирующего

преобразования UT среднеквадратичное расстояние между точками своего образа (в среднем для всех образов) составило величину 3,7 условных единиц. Следовательно, ориентировочно можно полагать, что отношение модуля разности координат центров тяжести произвольной пары образов к сумме среднеквадратичных отклонений в пространстве одномерных детерминистских признаков должно быть больше двух.

В результате эксперимента по одномерному детерминистскому критерию была найдена система из 6-ти признаков, позволяющих разделить центры тяжести образов с порогом d₀, равным 15 условным единицам.

В таблицах 8.8 и 8.9 представлены расстояния между центрами тяжести образов в метрике с в 6-мерном пространстве признаков, найденных по взвешенному дискриминантному критерию (для центров тяжести образов), и в 6-мерном пространстве признаков, найденных по одномерному детерминистскому критерию. Из сравнения таблиц видно, что для всех десяти пар центров тяжести, расстояния между которыми в метрике с в пространстве взвешенных дискриминантных признаков являются наименьшими (меньше 20 уел. ед.), одномерная разделимость в пространстве одномерных детерминистских признаков улучшилась. Наибольшее улучшение одномерной разделимости произошло для ближайших пар образов "два" и "ноль" (с 9 до 15,2 уел. ед.), "четыре" и "читаю" (с 12 до 19 уел. ед.), "один" и "три" (с 12 до 18 уел. ед.)

Этого результата можно было ожидать из сопоставления самих критериев создания признаков.

Взвешенный дискриминантный критерий является по существу многомерным и адекватен метрике /2. Четырехмерное подпространство первых четырех признаков, найденное по этому критерию, обеспечивает расстояние в метрике l₂ между центрами тяжести ближайшей пары образов "два" и "ноль", равное 14,8 условных единиц (см. рис. 8.6). Однако сами отдельно взятые признаки "отклонены" от направления вектора, соединяющего центры тяжести этих образов (для разделимости в метрике 12 в этом нет никакой необходимости).

Признаки, находимые по одномерному детерминистскому критерию, непосредственно направлены на отыскание отдельных направлений, обеспечивающих разделимость в метрике с.

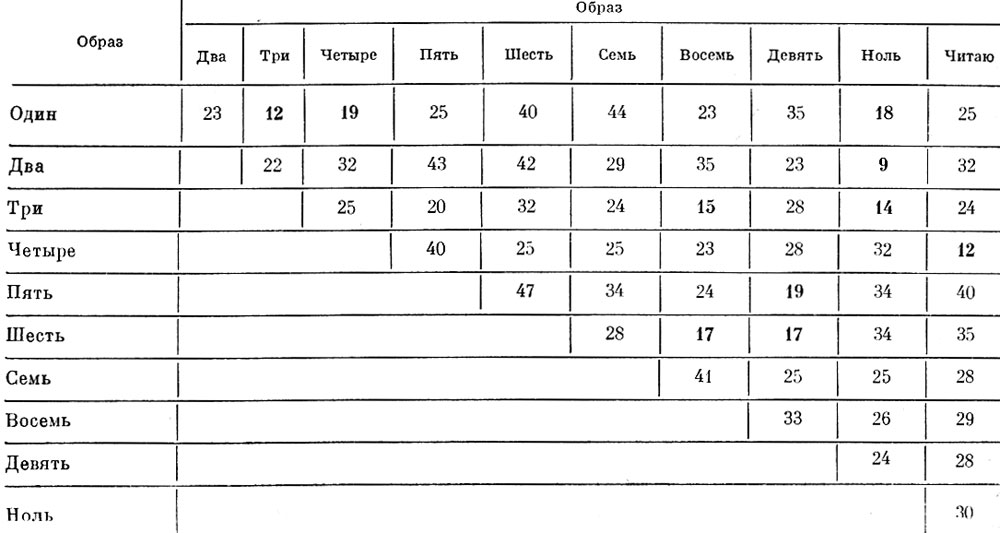
Таблица 8.8. Расстояния между центрами тяжести образов в метрике с в 6-мерном пространстве признаков, найденных по взвешенному дискриминантному критерию (для центров тяжести)

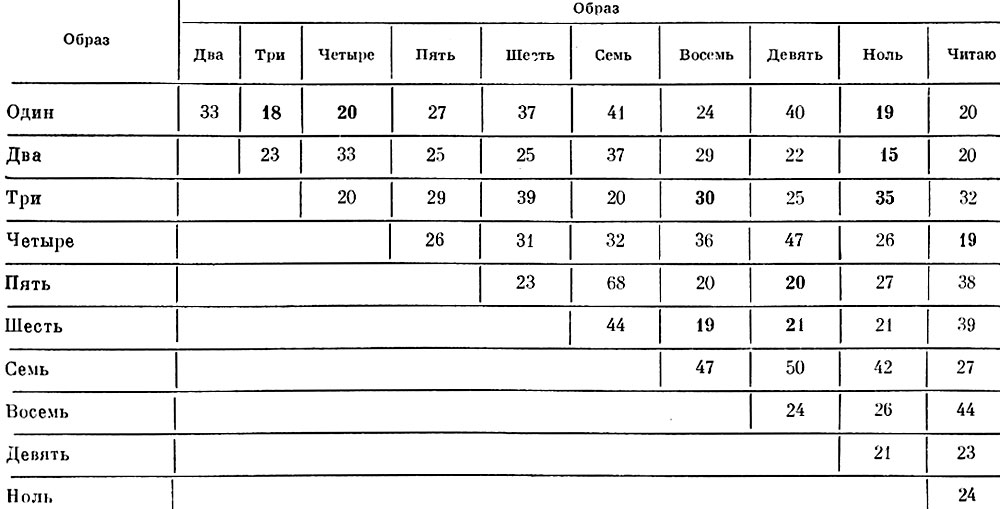
Таблица 8.9. Расстояния между центрами тяжести образов в метрике с в 6-мерном пространстве признаков, найденных по одномерному детерминистскому критерию (с порогом d₀ = 15 уел. ед. для центров тяжести образов)

После ортогонализации системы из шести признаков, найденных по одномерному детерминистскому критерию, расстояния между центрами тяжести образов в метрике l₂ оказались примерно такими же, как в шестимерном пространстве взвешенных дискриминантных признаков. Следовательно, оба шестимерных подпространства довольно "близки" друг к другу. Отличие между ними заключается лишь в выборе направлений координатных осей, которые важны с точки зрения разделимости в метрике с и безразличны для метрики l₂.