§ 8.3.3. Создание системы признаков

Для создания системы признаков оптимизировался взвешенный дискриминантный критерий (4.4.1) с инверсной весовой функцией (см. стр. 200).

Благодаря введению соответствующей весовой функции признаки, находимые по взвешенному дискриминантному критерию, в первую очередь разделяют центры тяжести близких пар образов. Степень разделимости реализаций различных образов по этим признакам зависит от того, насколько нормирование (с помощью преобразования U^T) разброса реализаций относительно центров тяжести образов, производимое в среднем по всем образам, нормирует разброс реализаций относительно каждого образа в отдельности.

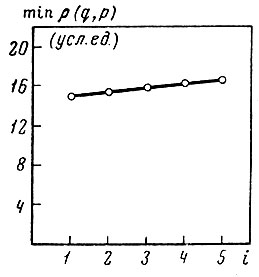
8.15. Зависимость минимального расстояния между центрами тяжести образов в метрике l₂ от размерности пространства признаков

Это условие является особенно важным для близких пар образов.

По статистическим характеристикам учебной выборки образов в пространстве исходного описания было выявлено, что наиболее близкими являются 1, 2 и 3-й образы. Остальные образы достаточно далеки друг от друга. Поэтому параметры преобразования U^T, нормирующего в среднем разброс реализаций относительно центров тяжести образов, находились только для 1, 2 и 3-го образов.

После нахождения признаков по взвешенному дискриминантному критерию было совершено преобразование массива учебной выборки в пространство признаков Y.

На рис. 8.15 представлен график изменения минимального расстояния между центрами тяжести образов в зависимости от увеличения размерности пространства признаков.

График показывает, что найденные признаки действительно в первую очередь направлены на разделение наиболее близких образов. ЭГо же иллюстрируют таблицы 8.11-8.15, в которых представлены расстояния между центрами тяжести образов в подпространствах, образованных первым признаком (табл. 8.11), двумя первыми признаками (табл. 8.12), тремя первыми признаками (табл. 8.13), четырьмя (табл. 8.14) и в полном десятимерном пространстве признаков (табл. 8.15).

Из таблиц видно, что уже только один первый признак "выбирает" 90% от расстояния между наиболее близкими образами. В силу того, что малое расстояние между образами учитывается с большим весом, добавление второго признака увеличивает расстояние только между наиболее близкими парами образов (I и II, I и III). Третий признак уже направлен на разделение следующей близкой пары образов (III и IV).

Интересно сравнить качество системы из трех взвешенных дискриминантных признаков с качеством десяти параметров исходного описания по критерию одномерной разделимости. В таблицах 8.16 и 8.17 представлены отношения расстояний между координатами центров тяжести наиболее близких пар образов (I и II, I и III) к сумме среднеквадратичных отклонений соответственно для пространства исходного описания и для трехмерного пространства признаков. Сопоставление этих таблиц показывает, что по сравнению с параметрами исходного описания мера одномерной разделимости по найденным признакам для наиболее близких образов увеличилась в два с лишним раза.

Матрица преобразования W̃^T параметров исходного описания X в трехмерное пространство признаков

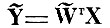
приведена в табл. 8.18.

Некоторые весовые коэффициенты преобразования W̃^T больше единицы. Напомним, что полное преобразование

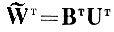
(см. главу IV), где В^т - матрица ортогонального преобразования, a U^T - матрица, осуществляющая косое сжатие для нормирования внутриклассовой дисперсии. Абсолютные расстояния в сокращенном пространстве признаков Ỹ могут увеличиться только за счет преобразований U^T. Однако преобразование U^T подобрано здесь так, чтобы суммарная дисперсия центров тяжести по всем осям полного пространства признаков

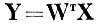
была такой же, как и в пространстве исходного описания X. Данные, приведенные в таблицах 8. 16 и 8. 17, вообще некритичны к любому линейному изменению масштабов по осям, так как в них фигурируют относительные величины.

Таблица 8.11. Расстояния между центрами тяжести образов в одномерном пространстве признаков

Таблица 8.12. Расстояния между центрами тяжести образов в метрике l₂ в двумерном пространстве признаков

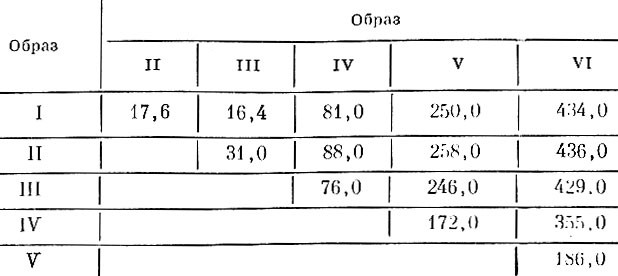
Таблица 8.13. Расстояния между центрами тяжести образов в метрике l₂ в трехмерном пространстве признаков

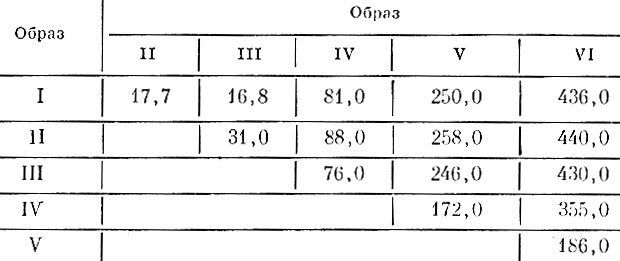
Таблица 8.14. Расстояния между центрами тяжести образов в метрике l₂ в четырехмерном пространстве признаков

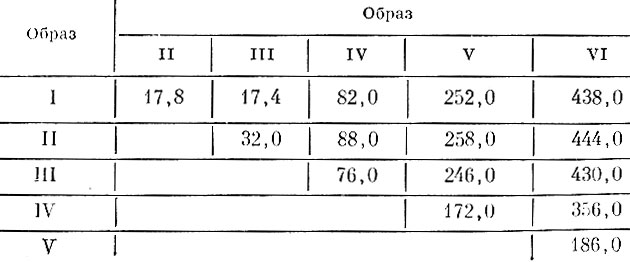
Таблица 8.15. Расстояния между центрами тяжести образов в метрике l₂ в 10-мерном пространстве признаков

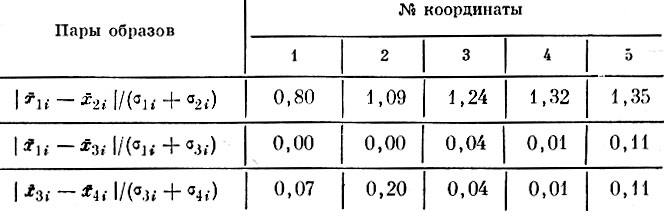
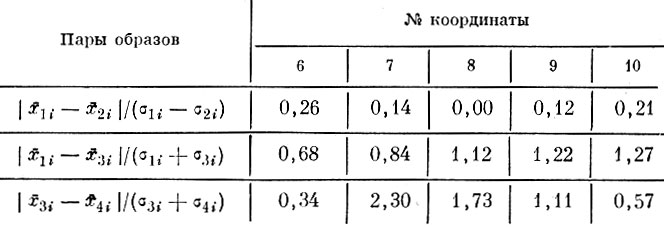
Таблица 8.16. Значения критерия одномерной разделимости в пространстве исходного описания

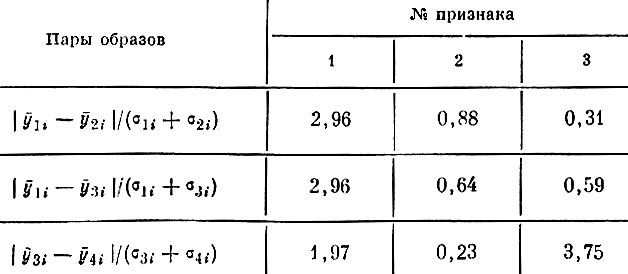
Таблица 8.17. Значения критерия одномерной разделимости в пространстве трех признаков, найденных по взвешенному дискриминантному критерию

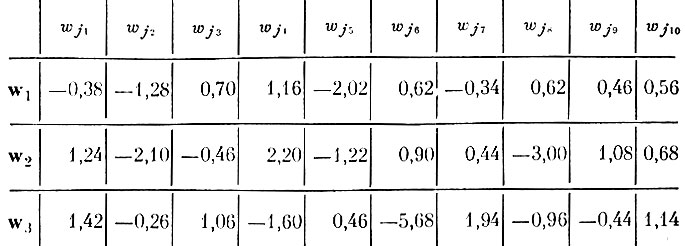
Таблица 8.18. Матрица признаков