§ 1.1. Разбиение части плоскости на 2n ячеек

Существует несколько способов разбиения части плоскости^* на 2ⁿ ячеек с помощью п фигур. Приведем некоторые из них.

Замкнутая кривая ψ_i без самопересечений делит плоскость на две части (ячейки) - внутреннюю и внешнюю (предполагаем, что кривая ψ_i - граница ячеек - не принадлежит ни одной из них), одну из ячеек (внутреннюю)_обозначим a_i, другую, дополняющую а_i до (части) плоскости, - ā_i, i = 1,...,n. Иногда в качестве - удобно использовать прямую, которая также делит плоскость на две части (ячейки).

При n = 1 в качестве можно взять окружность произвольного, но фиксированного радиуса (рис. 1.1) или прямую (рис. 1.2).

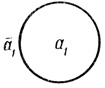
Рис. 1.1

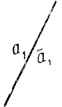
Рис. 1.2

При n > 1 замкнутые кривые ψ₁,...,ψ_n без самопересечений располагаются на плоскости так, чтобы разделить ее на 2ⁿ ячеек.

При n = 2 можно разделить плоскость на ячейки двумя окружностями (рис. 1.3) или двумя прямыми (рис. 1.4).

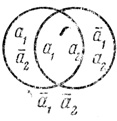
Рис. 1.3

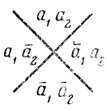
Рис. 1.4

При n = 3 еще можно воспользоваться тремя окружностями^* (рис. 1.5) или двумя прямыми и окружностью с центром в точке их; пересечения (рис. 1.6), но уже нельзя - тремя прямыми.

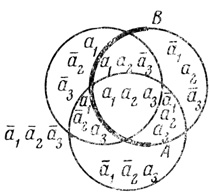
Рис. 1.5

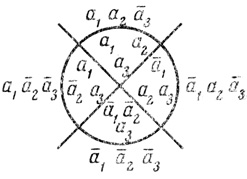
Рис. 1.6

^* (Для краткости вместо слов "часть плоскости" далее будем употреблять слово "плоскость".)

При n > 3 использовать только окружности нельзя. Действительно, предположим, что на плоскости расположены три окружности ψ₁, ψ₂, ψ₃ так, что плоскость делится на 8 ячеек (рис. 1.5). Невозможно' расположить на этой плоскости 4-ю окружность ψ₄ так, чтобы плоскость делилась на 16 ячеек, так как ψ₄ (для того, чтобы каждую из имеющихся 8 ячеек разделить пополам) должна была бы пересекать ψ₁, ψ₂, ψ₃ в 8 точках, но при любом расположении на трех окружностях 8 точек по крайней мере три из них лежат на одной окружности (рис. 1.7). Следовательно, должна была бы пересекать одну из трех ψ₁, ψ₂, ψ₃ окружностей, не совпадая с ней не менее чем в трех точках, что невозможно.

Наибольшее число ячеек, на которое могут разбить плоскость n окружностей, равно n² - n + 2 [22].

При n = 4 можно расположить на плоскости две прямые, окружность и эллипс так, что плоскость разделится на 2ⁿ ячеек (рис. 1.8).

Следовательно, при n = 1, 2, 3, 4 плоскость можно разделить на 2п ячеек с помощью п фигур, ограниченных кривыми без точек самопересечения. Перейдем к общему способу разбиения плоскости на 2ⁿ ячеек с помощью n фигур.

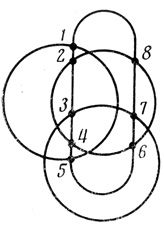
Рис. 1.7

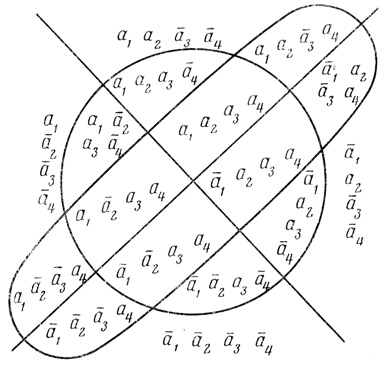
Рис. 1.8

Индуктивный способ разбиения плоскости на 2ⁿ ячеек.

1. При n = 1, 2, 3 способы разбиения окружностями указаны выше (рис. 1.1, 1.3, 1.5).

2. Предположим, что при n = k, k > 3 указано такое расположение k фигур, что плоскость делится на 2^k ячеек. Тогда для расположения k + 1 фигуры на этой плоскости достаточно

во-первых, выбрать незамкнутую кривую υ без точек самопересечения, т, е. незамкнутую кривую Жордана^*, принадлежащую границам всех 2^k ячеек и имеющую с каждой из этих границ только один общий кусок,

^* (Кривая Жордана есть геометрическое место точек плоскости: х = f(t), y = g{t), где функции f(t) и g(t) непрерывны.)

во-вторых, обвести φ замкнутой кривой Жордана %+1 так, чтобы кривая %+1 проходила через все 2k ячеек и пересекала границу каждой ячейки только два раза.

Таким образом, получится такое расположение n = k + 1 фигур, что плоскость разделится на 2k+1 ячеек.

Для расположения k + 2 фигур на плоскости достаточно за φ взять кусок границы k + 1 фигуры.

Например, пусть при n = 3 плоскость разделена на 8 ячеек (рис. 1.5). Для проведения кривой ψ₄ за φ можно взять дугу АВ (рис. 1.5, дуга АВ проведена жирной линией). Обведем φ замкнутой кривой Жордана ψ₄ (рис. 1.9), получим n = 4. Для расположения пятой фигуры за φ можно взять кривую CDEF (рис. 1.10).

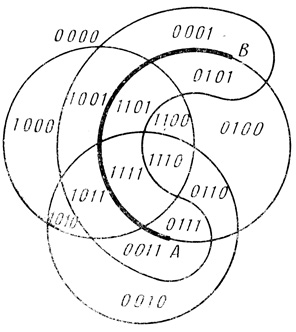
Рис. 1.9

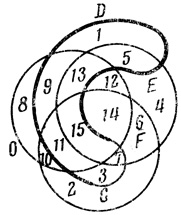
Рис. 1.10

На рис. 1.9 в ячейках плоскости расположены последовательности из n (n = 4) нулей и единиц; единица на j-том месте последовательности означает принадлежность ячейки фигуре a_i, нуль на j-том месте - принадлежность ячейки дополнению фигуры ау. Такие последовательности из п нулей и единиц можно воспринимать как числа в двоичной системе; в десятичной системе эти числа равны соответственно 0, 1,..., 2ⁿ - 1 (при n = 4 эти числа равны 0, 1,.., 15; см., рис. 1.10).

При индуктивном построении с ростом п площадь ячеек уменьшается.

Известны другие способы разбиения плоскости на 2ⁿ ячеек. Например, при разбиении плоскости по методу Минского - Сэлфриджа [23] площадь каждой ячейки не обязательно уменьшается с ростом n.

В методе Минского-Сэлфриджа при построении кривых ψ_i используются куски синусоид, период и амплитуда которых увеличиваются с ростом n: при n = 1 разбиение показано на рис. 1.11, при n = 2 - на рис. 1.12, при n = 3 - на рис. 1.13 и т. д.

Рис. 1.11

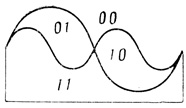
Рис. 1.12

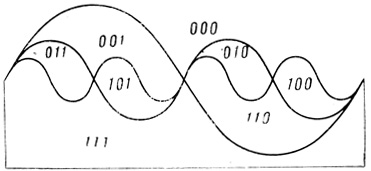
Рис. 1.13

Таблицы Венна. Очевидно, что с ростом n наглядность геометрических картинок уменьшается. Поэтому для больших n удобнее пользоваться таблицами, состоящими из 2ⁿ ячеек - таблицами Венна n переменных.

На рис. 1.14 приведена таблица Венна 5 переменных. Она содержит 32 ячейки. На левой стороне таблицы указаны все возможные комбинации фигур a₁, а₂ и их дополнений ā₁, ā₂, на верхней стороне - все возможные комбинации фигур а̄₃, а̄₄, а̄₅ и их дополнений a₃, а₄, а₅. Следовательно, для каждой ячейки таблицы можно однозначно определить, принадлежит она a_i или ā_i, i = 1,..., 5; так, ячейка, расположенная на пересечении 6-го слева столбца и 2-й сверху строки (на рис. 1.14 в этой ячейке поставлена звездочка), принадлежит ā₁, а₂, а₃, а̄₄, а₅.

На рис. 1.15 нриведена таблица Венна 6 переменных, в каждой ячейке которой расположена соответствующая последовательность из нулей и единиц (единица на j-том месте последовательности означает принадлежность ячейки фигуре а_i, нуль на i-том месте - принадлежность ячейки дополнению фигуры a_j) и десятичная запись числа, образованного этой последовательностью.

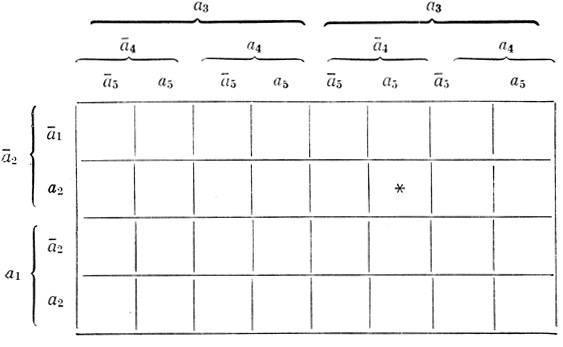
Рис. 1.14

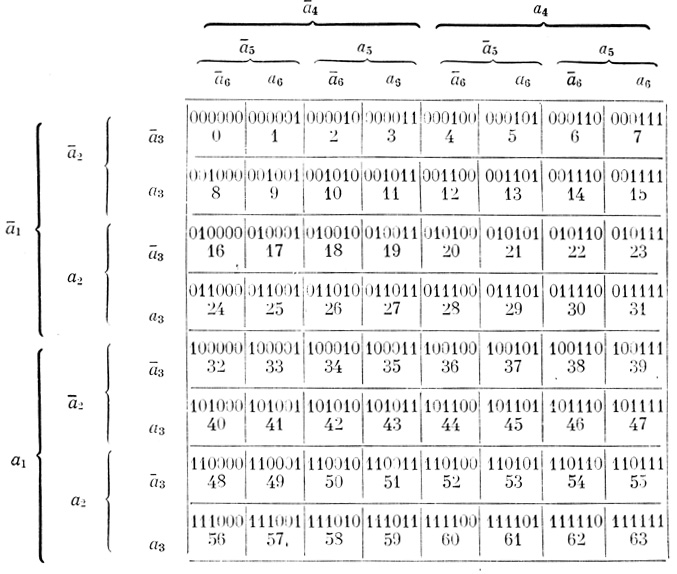
Рис. 1.15

Символ Венна. Для дальнейшего несущественно, каким образом получены 2ⁿ ячеек - разбиением плоскости или построением таблицы. Поэтому введем понятие символа Венна.

Символом Венна n переменных будем называть часть плоскости, состоящую из 2ⁿ ячеек, или таблицу Венна n переменных.

Ячейки символа Венна будем нумеровать числами 0, 1, ..., 2ⁿ-1, двоичная запись каждого из которых совпадает с соответствующей последовательностью из n единиц и нулей (единица на i-том месте последовательности означает принадлежность ячейки фигуре a_i, нуль на j-том месте - принадлежность ячейки дополнению фигуры a_j). Так, на рис. 1.10 в ячейках поставлены их номера при n = 4, а на рис. 1.15 - при n = 6.