§ 1.2. Диаграммы Венна в исчислении высказываний и операции над ними

Определение. Диаграммой Венна n переменных в исчислении высказываний будем называть символ Венна n переменных, в некоторых ячейках которого может быть поставлено по одной жирной точке^*.

^* (В дальнейшем для краткости заменяем слова "жирная точка" словом "точка".)

Диаграмму Венна n переменных будем обозначать через D^τ, иногда указывая справа в круглых скобках число переменных или сами переменные: D^τ(n) или D^τ (а₁,..., а_n).

Ячейки символа Венна перенумерованы, поэтому диаграмму Венна можно представлять в линейной форме в виде (β₀, β₁,...,β_2ⁿ-1) " где

- знак графического равенства, i = 0, 1,..., 2ⁿ - 1.

Пример 1.1. На рис. 1.16 приведена диаграмма Венна трех переменных D^τ(3). Точки находятся в 4-й и 7-й ячейках. В линейной форме D^τ(3)(-,-,-,-,⋅,-,-,⋅)

Операции над диаграммами.

1. Увеличение числа переменных (переход от n переменных к n + k переменным, k > 0). Пусть диаграмма D^τ(n) построена.

Пусть β₁,...,β_h, - все ячейки, в которых на D^τ(n) находятся точки.

Построим символ Венна n + k переменных, k > 0 (каждая ячейка диаграммы D^τ разделится на 2^k ячеек); во всех ячейках, на которые разбиваются β₁,...,β_h, и только в них поставим по одной точке; получим D^τ(n + k).

Пример 1.2. Пусть дана D^τ(2) (рис. 1.17). Построим D^τ(4) (рис. 1.18).

В дальнейшем при рассмотрении операций над несколькими диаграммами будем предполагать, что над ними проведена операция 1 и они содержат одинаковое число переменных.

Рис. 1.17

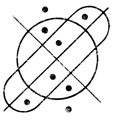
Рис. 1.18

2. Отрицание (дополнение). Пусть дана диаграмма D^τ(n).

Построим символ Венна n переменных. Во всех ячейках, в которых на D^τ(n) нет точек, поставим по одной точке; ячейки, в которых на D^τ(n) есть точки, остаются пустыми. Полученную диаграмму будем называть отрицанием диаграммы D^τ(n) и обозначать D^τ(n).

Пример 1.3. Пусть дана D^τ(4) (рис. 1.18). Построим D^τ(4) (рис. 1.19).

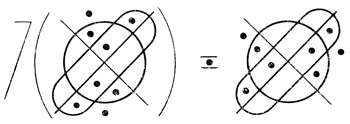
Рис. 1.19

3. Конъюнкция (пересечение). Пусть даны диаграммы D^τ₁(n) и D^τ₂(n).

Построим символ Венна n переменных. В тех и только в тех ячейках, в которых на D^τ₁ и на D^τ₂ одновременно находятся точки, поставим по одной точке. Полученную диаграмму будем называть конъюнкцией диаграмм D^τ₁(n) и D^τ₂(n) и обозначать (D^τ₁&D^τ₂).

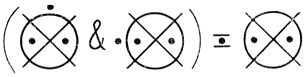
Рис. 1.20

Пример 1.4. Пусть D^τ₁,(-,-,-,⋅,-,⋅,⋅,-), (D^τ₂ (⋅,-,-,⋅,⋅,⋅,-,-,). Тогда (D^τ₁&D^τ₂ (-,-,-,⋅,-,⋅,-,-,)(рис. 1.20).

4. Дизъюнкция (объединение). Пусть даны диаграммы D^τ₁(n) и D^τ₂(n).

Построим символ Венна n переменных; во всех ячейках, в которых на D^τ₁ или на D^τ₂ находятся точки, и только в них поставим по одной точке; полученную диаграмму будем называть дизъюнкцией диаграмм D^τ₁ (n) и D^τ₂(n) и обозначать (D^τ₁∨D^τ₂).

Пример 1.5.

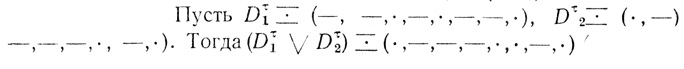
(рис. 1.21)

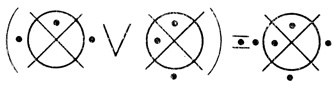
Рис. 1.21