§ 1.3. Соответствие между диаграммами и формулами исчисления высказываний
Между диаграммами Венна в исчислении высказываний и формулами исчисления установим соответствие. Предварительно напомним некоторые наиболее часто встречающиеся понятия; подробное изложение исчисления высказываний содержится в литературе по математической логике, например [24, 25].
Определение формул исчисления. Рассматривается алфавит, состоящий из переменных: a1,...,an, логических знаков:  , &, ∨, ⊃ и скобок: ( , ).
, &, ∨, ⊃ и скобок: ( , ).
Формулы определяются следующими правилами:
1. Если а - переменная, то а - формула.
2. Если Φ - формула, то  - формула.
- формула.
3. Если Φ1 и Φ2 -формулы, то (Φ1 & Φ2), (Φ1 ∨ Φ2) и (Φ1 ⊃ Φ2) - формулы.
Определение индуктивно, что позволяет переходить от уже известных формул к дальнейшим.
С каждой формулой можно связать некоторую функцию, значения которой равны 1 или 0 и которая определена для всевозможных наборов значений аргументов, принимающих также два значения: 1 и 0; 1 обозначает "истину" или "да", 0 - "ложь" или "нет". Функции, связанные только с логическими знаками  , &, ∨ и ⊃, называют элементарными. Элементарные функции определяются с помощью таблиц 1.1-1.4.
, &, ∨ и ⊃, называют элементарными. Элементарные функции определяются с помощью таблиц 1.1-1.4.
По этим таблицам для любого заданного набора значений независимых переменных (аргументов) можно найти соответствующее значение функции, заданной некоторой формулой. Легко видеть, что n независимых переменных принимают только 2n значений. Значения независимых переменных и соответствующие значения функции можно представить в виде таблицы, называемой таблицей истинности. Так как каждому набору значений аргументов сопоставляется только одно из чисел 1 или 0, то число всех различных функций, зависящих от n аргументов, равно 22n.
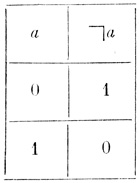
Таблица 1.1
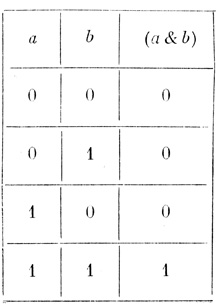
Таблица 1.2
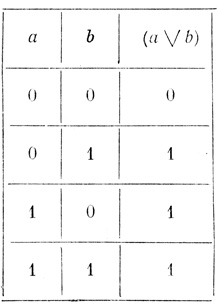
Таблица 1.3
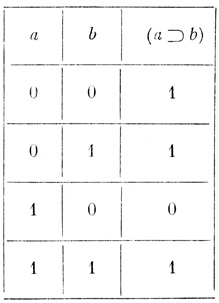
Таблица 1.4
Две формулы Φ1 и Φ2, составленные* из одних и тех же переменных, называются эквивалентными- (записываем Φ1 = Φ2), если их таблицы истинности имеют один и тот же столбец значений.
* (Формула Φ называется составленной из переменных ai1....,aik, если никакая переменная, отличная от ai1....,aik , не входит в Φ. Например (а3 ∨( a4⊃a5)) есть формула, составленная из переменных а1, а3, а4, а5, a8.)
a4⊃a5)) есть формула, составленная из переменных а1, а3, а4, а5, a8.)
Пример 1.6. Формулы Φ (
( (а2∨
(а2∨ a3) & (a1⊃a2), Φ1
a3) & (a1⊃a2), Φ1 (
( (а1∨а2)& а3) эквивалентны, так как их таблицы истинности имеют один и тот же столбец значений (в табл. 1.5 и 1.6 последние столбцы совпадают).
(а1∨а2)& а3) эквивалентны, так как их таблицы истинности имеют один и тот же столбец значений (в табл. 1.5 и 1.6 последние столбцы совпадают).
Формулу Φ называют дизъюнктивной нормальной (ДНФ), если Φ есть дизъюнкция конъюнкций, членами которых являются переменные и отрицания переменных.
Если Φ1 - формула, Φ2 - дизъюнктивная нормальная формула и формулы Φ1, Φ2 эквивалентны, Φ1 ≡ Φ2, то Φ2 называют дизъюнктивной нормальной формой формулы Φ1.
Дизъюнктивную нормальную формулу Φ называют совершенной (СДНФ), если в каждый ее дизъюнктивный член входят все различные переменные (быть может с отрицанием) формулы Φ, при этом каждая переменная может входить только один раз.
Построение формул по диаграммам Венна. Дана диаграмма Dτ(a1,..., аn).
Пусть β1,..., βh - все различные ячейки, в которых на Dτ(a1, ..., аn) находятся точки. Ячейка βi есть ãi1... ãin, где
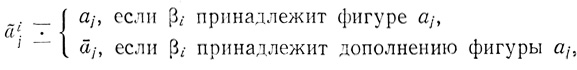
Ячейке βш поставим в соответствие формулу*
* (Некоторые скобки в формулах опускаем в силу ассоциативности как конъюнкции, так и дизъюнкции.)
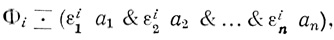
где
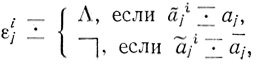
Λ - обозначение пустого слова j = 1,....,n, i = 1,...,h.
Диаграмме Dτ (a1,....,an) поставим в соответствие СДНФ (Φ1∨Φ2∨...∨Φh). Формулу, соответствующую диаграмме Dτ, будем обозначать Φ[Dτ].
Пример 1.1 (продолжение). По диаграмме Dτ(a1, a2, a3) (рис. 1.16) построим формулу*
Φ[Dτ(a1, a2, a3) (a1ā2ā3∨a1a2a3)
(a1ā2ā3∨a1a2a3)
 (a1ā2ā3∨a1a2a3)
(a1ā2ā3∨a1a2a3)
* (В СДНФ будем заменять  ai на āi, опускать & и все скобки, кроме внешних.)
ai на āi, опускать & и все скобки, кроме внешних.)
Если диаграмма Dτ(a1,..., аn) не содержит точек, то в соответствие ей ставим тождественно ложную формулу, например (a1 & a1).
a1).
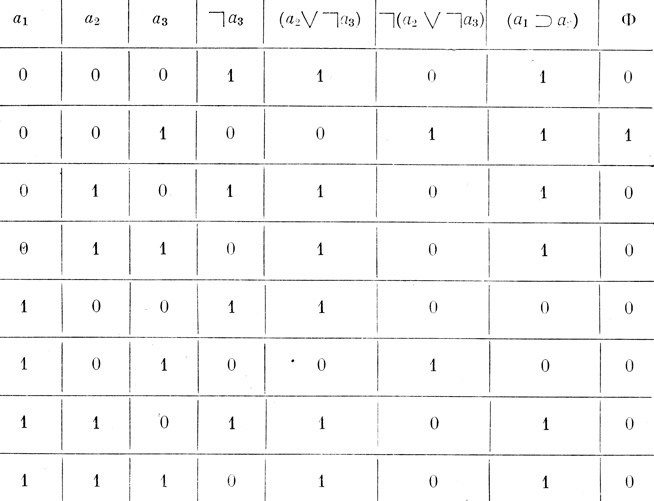
Таблица 1.5
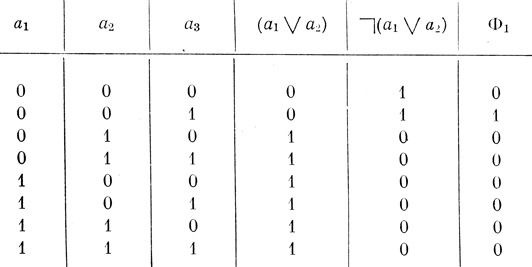
Таблица 1.6
Если на диаграмме число ячеек, занятых точками, больше числа пустых ячеек, то для уменьшения логической длины* удобнее начинать построение с пустых ячеек диаграммы и в соответствие диаграмме Dτ (a1,..., аn) ставить формулу  (Φh+1∨....∨Φ2n) не являющуюся ДНФ. При этом используется эквивалентность
(Φh+1∨....∨Φ2n) не являющуюся ДНФ. При этом используется эквивалентность
* (Логической длиной формулы называется число всех вхождений логических знаков в эту формулу.)
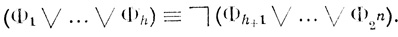 (1.1)
(1.1)
Для примера возьмем диаграмму Dτ(а1, а2, а3), расположенную справа от знака  на рис. 1.21. Логическая длина формулы (Φ1 ∨... ...∨Φh)
на рис. 1.21. Логическая длина формулы (Φ1 ∨... ...∨Φh)  (а̄1а̄2а̄3 ∨ а̄1а2а̄3 ∨ a1ā2ā3 ∨ а1а̄2а3 ∨ a1a2a3) равна 22, а логическая длина формулы (Φh+1 ∨...∨Φ2n)
(а̄1а̄2а̄3 ∨ а̄1а2а̄3 ∨ a1ā2ā3 ∨ а1а̄2а3 ∨ a1a2a3) равна 22, а логическая длина формулы (Φh+1 ∨...∨Φ2n) (а̄1а̄2а̄3 ∨ а̄1а2а3 ∨ а1а2а̄3) равна 12. Поэтому
(а̄1а̄2а̄3 ∨ а̄1а2а3 ∨ а1а2а̄3) равна 12. Поэтому
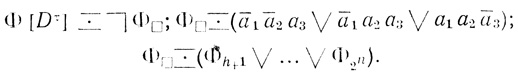
Построение диаграмм по данным формулам. Пусть, наоборот, дана не диаграмма Венна, а формула Φ исчисления высказываний, составленная из переменных а1,...,аn. Требуется построить диаграмму Венна, соответствующую формуле Φ. Диаграмму, соответствующую данной формуле Φ, будем обозначать Dτ[Φ].
Определение диаграммы, соответствующей данной формуле Φ:
а) каждой переменной аi формулы Φ поставим в соответствие следующую диаграмму Венна:
Построим символ Венна n переменных. Во всех ячейках i-той фигуры, и только в них, поставим по одной точке. Получим диаграмму, соответствующую переменной аi, Dτ[ai];
б) каждому логическому знаку формулы Φ поставим в соответствие операции (одну или две) над диаграммами Венна:
1. Предположим, что  Φ1 - подформула* формулы Φ и что диаграмма Dτ[
Φ1 - подформула* формулы Φ и что диаграмма Dτ[ Φ1] построена. Построим диаграмму Dτ[
Φ1] построена. Построим диаграмму Dτ[ Φ1].
Φ1].
* (Понятие "подформулы" данной формулы определяется следующим образом:
Диаграмму Dτ [ Φ1] определим как результат операции отрицания диаграммы Dτ[Φ1], записываем
Φ1] определим как результат операции отрицания диаграммы Dτ[Φ1], записываем
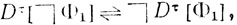 (1.2)
(1.2) где ↔ - знак, обозначающий равенство по определению.
1) если Φ - формула, то Φ является подформулой формулы Φ;
2) если Φ - формула, то подформулы формулы Φ являются подформулами формулы  Φ;
Φ;
3) если Φ1 и Φ2 - формулы, то подформулы формул Φ1 и Φ2 являются подформулами формул (Φ1 & Φ2), (Φ1 ∨ Φ2) и (Φ1 ⊃ Φ2).)
2. Предположим, что (Φ1 & Φ2), (Φ1v∨vΦ2) и (Φ1 ⊃ Φ2) - подформулы формулы Φ и что диаграммы Dτ[Φ1] и Dτ[Φ2] построены. Построим диаграммы Dτ[(Φ1&Φ2),Dτ[(Φ1∨Φ2)] и Dτ[Φ1⊃Φ2]*:
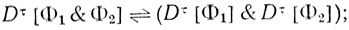 (1.3)
(1.3)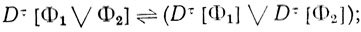 (1.4)
(1.4) 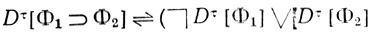 (1.5)
(1.5)* (В дальнейшем в аналогичных выражениях для краткости внешние круглые скобки формул будем опускать.)
Описанный способ определения диаграммы, соответствующей данной формуле Φ, имеет вид индуктивного построения. На первом шаге (пункт "а") строятся диаграммы, соответствующие всем графически различным переменным формулы Φ. Индукция ведется по шагам построения формулы Φ (пункт "б").
Нетрудно доказать, что для любой формулы Φ1 не являющейся тождественно ложной, формул Φ2 [Dτ[Φ1]] есть совершенная дизъюнктивная нормальная форма формулы Φ1 (при этом формулы пишутся по ячейкам, занятым точками).
Пример 1.6. (продолжение). Построим диаграмму Венна формулы
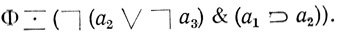
В данную формулу входят три графически различных переменных a1, а2, а3. Поэтому чертим символ Венна не менее трех переменных. Например, возьмем символ Венна трех переменных (рис. 1.6). Диаграммы Венна будем представлять в линейной форме.
Прежде всего построим диаграммы, соответствующие переменным а1, а2 и а3:

Построим диаграмму, соответствующую  a3.
a3.
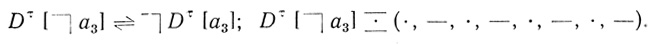
Построим диаграмму, соответствующую (a2∨ а3):
а3):
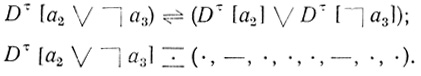
Построим диаграмму, соответствующую  (a2∨
(a2∨ a3):
a3):
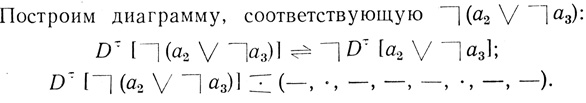
Построим диаграмму, соответствующую (а1 ⊃ а2):
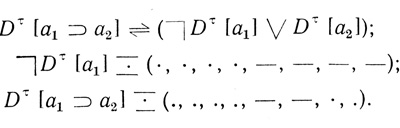
Наконец, построим диаграмму формулы Φ:
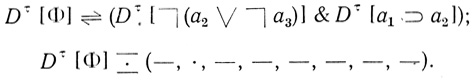
Построим формулу, соответствующую Dτ[Ф], - ( а1 &
а1 &  а2 & а3). Эта формула является совершенной дизъюнктивной нормальной формой исходной формулы Φ и также формулы Φ1
а2 & а3). Эта формула является совершенной дизъюнктивной нормальной формой исходной формулы Φ и также формулы Φ1 Z(
Z( (a1 ∨ а2) & а3) (см. начало этого примера).
(a1 ∨ а2) & а3) (см. начало этого примера).
В силу установленного соответствия между диаграммами Венна и формулами исчисления высказываний можно говорить о геометрическом (диаграммном) построении исчисления высказываний.
Диаграммы Венна можно использовать при решении некоторых задач. Покажем, как на диаграммах Венна решается проблема разрешения для формул исчисления высказываний, опишем способ, позволяющий на диаграммах принципиально обозреть все возможные попарно неэквивалентные логические следствия из данных посылок, выразимых на языке исчисления высказываний. При этом вопрос о логических следствиях изучается вплоть до обзора всех простых нетривиальных - в определенном смысле - следствий.
В следующих параграфах настоящей главы остановимся на вопросах, тесно связанных с избыточностью формул исчисления высказываний.
Проблема разрешения. Нетрудно доказать, что формула Φ универсально общезначима (тождественно истинна) тогда и только тогда, когда в каждой ячейке диаграммы Dτ[Φ] находится по одной точке.
Например, формула Φ ((а ⊃(b ⊃ с)) ⊃ ((а & b) ⊃ c)) универсально общезначима, так как Dτ [Φ](⋅,⋅,⋅,⋅,⋅,⋅,⋅,⋅).
((а ⊃(b ⊃ с)) ⊃ ((а & b) ⊃ c)) универсально общезначима, так как Dτ [Φ](⋅,⋅,⋅,⋅,⋅,⋅,⋅,⋅).
Вывод логических следствий.
Определение. Формулу Ψ называют логическим следствием из посылок Φ1, . . . , Φm тогда и только тогда, когда ((Φ1 & ... & Φm) ⊃ Ψ) есть тождественно истинная формула.
Покажем, что формула Ψ будет логическим следствием посылок Φ1, ..... , Φm тогда и только тогда, когда на диаграмме Dτ[Ψ] n переменных, где n - число графически неравных переменных формулы (Φ1 & ... & Φm), во всех ячейках, в которых на диаграмме Dτ[Ф1 & ... & Φm] n переменных есть точки, содержатся точки.
1. Пусть Ψ есть логическое следствие формул Φ1, . . . , Φm. Докажем, что все точки диаграммы Dτ[Φ1 & ... & Φm] перенесены на диаграмму Dτ[Ψ] в те же ячейки.
Предположим, что в ячейках α1, . . . , αk на Dτ[Φ1 & ... & Φm] есть точки, а на Dτ[Ψ] - нет. Тогда и на диаграмме Dτ[(Φ1 ... & Φm) ⊃ Ψ] n переменных ячейки α1, . . . ,αk пусты, но ((Φ1 & ... & Φm) ⊃ Ψ) есть тождественно истинная формула. Следовательно, если Ψ логическое следствие посылок Φ1, . . . , Φm, то все точки диаграммы Dτ[Φ1 &. . . . . . & Φm] содержатся на диаграмме Dτ[Ψ] в тех же ячейках, что и на Dτ[Φ1 & ... & Φ1].
2. Пусть все точки диаграммы [Φ1 & ... & Φm] перенесены на некоторую диаграмму Dτ(n), тогда формула Ψ, соответствующая получившейся из Dτ(n) диаграмме, есть логическое следствие из формул Φ1, . . . , Φm, так как в каждой ячейке диаграммы Dτ[(Φ1 & ... & Φm) ⊃ Ψ] n переменных содержится по одной точке.
Таким образом, для получения логического следствия из посылок Φ1, . . . , Φm, составленного из δ переменных, где δ>n, n - число графически неравных переменных формулы (Φ1 & . .. ... & Φm), надо построить диаграмму Dτ[Φ1 & . . . . .. . & Φm] n переменных, в некоторых из пустых ячеек диаграммы Dτ[Φ1& ... & Φm] поставить по одной точке, написать формулу, соответствующую полученной диаграмме, которая и будет логическим следствием посылок Φ1, . . . , Φm.
Проставляя точки в различных пустых ячейках диаграммы Dτ[Φ1& ... & Φm], будем получать различные логические следствия из Φ1,. . . , Φm. Перебирая все возможные комбинации пустых ячеек диаграммы Dτ[Φ1& ... &Φm], получим все возможные попарно неэквивалентные следствия из Φ1, . . . , Φm, составленные из 6 переменных.
Простые логические следствия. Среди всех логических следствий посылок Φ1,. . . , Φm выделим простые следствия.
Определение. Логическое следствие Ψ посылок Φ1,....,Φm называют простым, если Ψ есть дизъюнкция переменных (может быть с отрицанием), не поглощаемая никаким другим логическим следствием того же вида.
Конъюнкцию всех простых логических следствий посылок Φ1, ..... .... , Φm называют силлогистическим многочленом формулы (Φ1 & ... & Φm).
Пусть а1, . . . , аn - все графически неравные переменные формулы (Φ1 & ... & Φm).
1. Если на диаграмме Dτ[Φ1 & . . . & Φm] n переменных находится только одна точка, то ε1a1, . . . , εnan - все простые логические следствия посылок Φ1 . . . , Φm (где ε1 - пустое слово или  ; εi
; εi Λ , если точка лежит в ячейке, принадлежащей фигуре ai;εi
Λ , если точка лежит в ячейке, принадлежащей фигуре ai;εi
 если точка лежит в ячейке, принадлежащей дополнению фигуры аi) и (ε1a1 & ε2a2 & ... & εnan) - силлогистический многочлен формулы (Φ1 & ... & Φm).
если точка лежит в ячейке, принадлежащей дополнению фигуры аi) и (ε1a1 & ε2a2 & ... & εnan) - силлогистический многочлен формулы (Φ1 & ... & Φm).
2. Пусть на диаграмме Dτ[Φ1. . . &Φm] находится больше, чем одна точка. Пусть Ψ - логическое следствие посылок Φ1, . . . , Φm.
Если на диаграмме Dτ[Ψ] точки находятся только во всех ячейках фигуры aγβ1β1∪........∪aγβkβk (где γβk - одно из чисел 2, 3: γβi 3, если точки лежат во всех ячейках, принадлежащих фигуре aβi; γβi
3, если точки лежат во всех ячейках, принадлежащих фигуре aβi; γβi 2, если точки лежат во всех ячейках, принадлежащих дополнению фигуры aβi) формула Ψ эквивалентна формуле (εβ1aβ1∨....∨εβkaβk), где εβk
2, если точки лежат во всех ячейках, принадлежащих дополнению фигуры aβi) формула Ψ эквивалентна формуле (εβ1aβ1∨....∨εβkaβk), где εβk Λ если γβi
Λ если γβi 3; εβi
3; εβi
 если γβi
если γβi 2, и (εβ1aβ1∨..........∨εβkaβk) - логическое следствие посылок Φ1, . . . , Φm, состоящее из k переменных.
2, и (εβ1aβ1∨..........∨εβkaβk) - логическое следствие посылок Φ1, . . . , Φm, состоящее из k переменных.
3. Если Ψ1, Ψ2 - такие логические следствия посылок Φ1, . . . , Φm, что Dτ[Ψ1] ∈ Dτ[Ψ2], то формула Ψ2 поглощается формулой Ψ1 где Dτ[Ψ1], Dτ[Ψ2] - диаграммы одинакового числа переменных.
4. Если Ψ1,.......,Ψr - все возможные графически различные (т. е. имеющие различные диаграммы Венна n переменных, а следовательно, попарно неэквивалентные) простые логические следствия посылок Φ1, . . . , Φm, то (Dτ[Ψ1] & . . . &Dτ [Ψr])  Dτ[Φ1&. . .& Φ2], (Ψ1 & ... & Ψr) - силлогистический многочлен формулы (Φ1 & ... & Φm).
Dτ[Φ1&. . .& Φ2], (Ψ1 & ... & Ψr) - силлогистический многочлен формулы (Φ1 & ... & Φm).
5. Сформулируем способ нахождения простых логических следствий посылок Φ1, .. . , Φm.
Берутся Ψ1,. . . , Ψl - все возможные графически различные простые логические следствия из Φ1,. . . , Φm, составленные из одной переменной.
Если (Dτ[Ψ1]& . . . & Dτ [Ψl])  Dτ [Φ1 & ... & Φm], то (Ψ1 & ... & Ψl) - силлогистический многочлен формулы (Φ1 &...& Φm).
Dτ [Φ1 & ... & Φm], то (Ψ1 & ... & Ψl) - силлогистический многочлен формулы (Φ1 &...& Φm).
Если (Dτ[Ψ1] & . . . &Dτ[Ψl] отлична от Dτ[Φ1 & ... & Φm] (при этом рассматриваются диаграммы одинакового числа переменных), то берутся Ψl+1,. . . , Ψl1 - всевозможные графически различные следствия из Φ1, . . . , Φm, составленные из двух переменных, такие, что для любого i (i = 1, ..., l) и для любого j (j = l + 1,.....,l1) Dτ[Ψi] ∉ Dτ[Ψj].
Если (Dτ[Ψ1]& ... & Dτ[Ψl1])  Dτ[Φ1,.....,Φm], то (Ψ1&......&Ψl1) - силлогистический многочлен формулы (Φ1&... &Φm).
Dτ[Φ1,.....,Φm], то (Ψ1&......&Ψl1) - силлогистический многочлен формулы (Φ1&... &Φm).
Если (Dτ[Ψ1]&...&Dτ [Ψl1]) отлична от Dτ [Φ1&... & Φm], то берутся Ψl1+1,......,Ψl2 - все различные логические следствия из Φ1,..., Φm, составленные из трех переменных, такие, что для любого i (i = 1,..., l1) и для любого j(j = l1 + 1,..., l2) Dτ[Ψi]∉Dτ[Ψj], и т. д., пока не найдется такое k, что (Dτ[Ψi] &... ... & Dτ[Ψk]) Dτ [Φ1&... &Φm], тогда Ψ1,...,Ψk - силлогистический многочлен формулы (Φ1&... &Φm).
Dτ [Φ1&... &Φm], тогда Ψ1,...,Ψk - силлогистический многочлен формулы (Φ1&... &Φm).
Примеры:
1.7. Пусть Dτ [Φ1&...&Φm] (-,⋅,⋅,-).
(-,⋅,⋅,-).
а) Все логические следствия: (-, ⋅, ⋅,-), (-, ⋅, ⋅, ⋅), (⋅, ⋅, ⋅, -), (⋅, ⋅, ⋅, ⋅).
б) Простые логические следствия: (-,-, ⋅, ⋅) соответствует формула (а1 ∨ а2), (⋅,⋅,⋅,-) - ( а1 ∨
а1 ∨  a2)
a2)
1.8. Пусть Dτ [Φ1 &... &Φm]  (-, -, ⋅,-, -, -,-).
(-, -, ⋅,-, -, -,-).
Простые логические следствия:
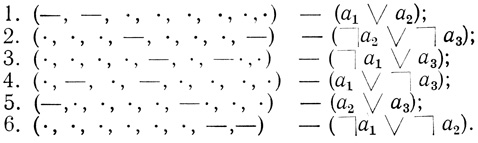
Отметим, что силлогистический многочлен формулы Φ не является минимальным по логической длине среди конъюнктивных нормальных форм формулы Φ. Так, в последнем примере формула (Φ1& ... & Φm) эквивалентна формуле ((а1∨a2) & ( а2∨
а2∨ a3)& ...... & (
a3)& ...... & ( a1∨a3)), если брать первые три диаграммы; формула (Φ1&......&Φm) (эквивалентна формуле ((a1 ∨
a1∨a3)), если брать первые три диаграммы; формула (Φ1&......&Φm) (эквивалентна формуле ((a1 ∨  а3) & (а2 ∨ а3) &(
а3) & (а2 ∨ а3) &( а1 ∨
а1 ∨  а2)), если брать последние три диаграммы.
а2)), если брать последние три диаграммы.
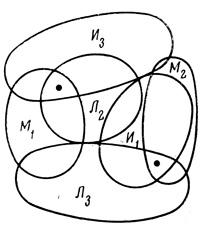
Рис. 1.22
Иногда при решении задач нет необходимости рассматривать все 2n ячеек символа Венна.
Для примера возьмем задачу.
При составлении расписания уроков на определенный день преподаватели высказали пожелания, чтобы их уроки были: по математике - первым или вторым, по истории - первым или третьим, по литературе - вторым или третьим. Можно ли удовлетворить пожелания всех трех учителей?
Пусть М1 и М2 - пожелания математика, И1 и И3 - пожелания историка, Л2 и Л3 - пожелания литератора. Тогда в силу несовместности некоторых из переменных можно ограничиться только 18 ячейками из 64. Соответствующая диаграмма Венна приведена на рис. 1.22. Из диаграммы видно, что пожелания учителей можно удовлетворить, расположив уроки в следующем порядке: математика, литература, история или история, математика, литература.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'