§ 1.4. Сети диаграмм Венна в исчислении высказываний

Как известно, краткость принадлежит к числу бесспорных достоинств хорошего изложения предмета. Бывают, однако, случаи, когда, наоборот, существенную роль играет избыточность информации. Именно за счет такой избыточности и может быть обеспечена, как будет показано в этой работе, надежность системы, состоящей из относительно ненадежных элементов.

Чтобы предварительно пояснить, в чем тут дело, вернемся к при меру 1.6. Две формулы:

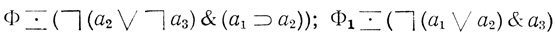
эквивалентны. Однако формула Φ содержит больше логических знаков, чем формула Φ₁. В этом случае говорят, что формула Φ является избыточной по сравнению с формулой Φ₁.

Аналогично формулы

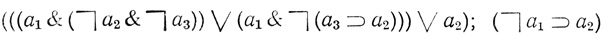
эквивалентны. Однако первая формула содержит большее число переменных и знаков операций, чем вторая, и ее значение не зависит от того, какое значение принимает переменная а₃. В этом случае также говорят, что первая формула является избыточной. Информацию, которую несет первая формула, можно выразить, таким образом, с помощью гораздо более короткой формулы.

Если в какую-нибудь формулу, содержащую n различных переменных, на место этих переменных поставить какие-нибудь формулы от тех же переменных, то получим новую формулу от этих n переменных, в которую в свою очередь можем подставить на место переменных какие-нибудь новые формулы от тех же переменных, и т. д. Каждая такая формула представляет собой некоторую функцию от ее переменных. Но различных функций от n переменных только 2²ⁿ; представляющих же эти функции формул, можно написать сколь угодно много. Вот и получается избыточность информации о функции, задаваемой с помощью формулы. Распоряжаться такой избыточностью будем с помощью сетей диаграмм Венна.

Между диаграммами Венна и функциями n переменных легко устанавливается соответствие.

Отметим, что

1) каждой ячейке β_i диаграммы Венна n переменных соответствует только один набор значений n независимых переменных, при этом номер ячейки β_i, записанный в двоичной системе, совпадает с соответствующим набором значений переменных;

2) на диаграмме Венна формулы Φ в ячейке β_i - тогда и только тогда находится точка, когда значение формулы Φ, соответствующее набору значений переменных, который совпадает с номером ячейки β_i в двоичной системе, равно единице.

3) две формулы Φ₁ и Φ₂, составленные из одних и тех же переменных, эквивалентны тогда и только тогда, когда их диаграммы Венна n переменных графически совпадают.

Выше в диаграммах Венна n переменных предполагалось, что все n переменных независимы. Теперь при одновременном рассмотрении нескольких диаграмм снимем для некоторых из них требование независимости переменных; будем говорить, что все рассматриваемые диаграммы образуют сеть.

Описание строения сетей диаграмм. Каждая сеть состоит из нескольких рядов (рангов) диаграмм. Диаграммы первого ранга являются входными диаграммами, диаграммы последнего ранга - выходными.

Каждая диаграмма, начиная со второго ранга, связана кривыми с одной или несколькими диаграммами сети, на которых эти кривые начинаются. Кривые оканчиваются стрелками на диаграммах. Все кривые данной диаграммы нумеруются.

Номера ставятся слева от стрелки. Число кривых, оканчивающихся на данной диаграмме, равно числу различных переменных этой диаграммы.

Каждую диаграмму сети будем рассматривать как некоторый оператор, функционирование которого ведет к построению диаграммы Венна независимых переменных. Последнюю будем называть результирующей диаграммой оператора (правила построения результирующих диаграмм операторов даны ниже).

Обозначения: D^τ_r,i- диаграмма Венна, расположенная в r-том ранге на i-том месте (ранги нумеруются сверху вниз, диаграммы в ранге - слева направо); [D^τ_r,i] - результирующая диаграмма оператора D^τ_r,i.

Результирующие диаграммы операторов последнего ранга сети будем называть результирующими диаграммами сети. Их число совпадает, с числом выходных диаграмм сети. Сеть называем одновыходной, если в последнем ранге находится только одна диаграмма.

В настоящем параграфе ограничимся случаем, когда кривые начинаются только на диаграммах вышестоящих рангов и когда на диаграммах первого ранга кривые не могут оканчиваться. В § 1.6 разбирается более общий случай.

Одноранговые сети. Каждая диаграмма n переменных является одноранговой сетью с одним выходом. Результирующей диаграммой такой сети считаем данную диаграмму или результат операции 1 над данной диаграммой (при увеличении числа переменных). В последнем случае результирующую диаграмму помещаем в квадратных скобках справа от оператора.

Пример 1.2 (продолжение). На рис. 1.17 расположена одноранговая сеть с одним выходом, результирующая диаграмма совпадает с данной диаграммой. На рис. 1.23 - эта же сеть с результирующей диаграммой четырех переменных (для сравнения см. рис. 1.18).

k диаграмм соответственно n₁,...,n_k переменных, расположенных в одном ранге, образуют одноранговую сеть с к выходами. Результирующие диаграммы каждого из операторов строятся независимо от остальных. Иногда требуется, чтобы все результирующие диаграммы были диаграммами n переменных, n > max {n₁,...,n_k}. Пример 1.9. На рис. 1.24 дана одноранговая сеть с двумя выходами, n₁ = 2, n₂ = 3, n = 4.

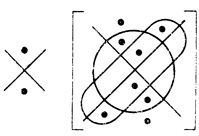
Рис. 1.23

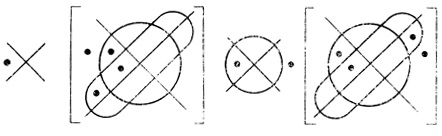
Рис. 1.24

Двухранговые сети с одним выходом. Первый ранг образуют k диаграмм соответственно n₁..., n_k переменных.

Диаграммы этого ранга называются входными.

Во втором ранге находится одна выходная диаграмма n_k+1 переменных, на которой оканчиваются стрелками n_k+1 кривых, начинающихся на диаграммах первого ранга. Все кривые перенумерованы (см., например, рис. 1.25). Если каждая диаграмма первого ранга связана только одной кривой с выходной диаграммой (в этом случае n_k+1 = k), и нумерация кривых совпадает с нумерацией всех диаграмм первого ранга (слева направо), то кривые чертить на рисунках не будем (см., например, рис. 1,26, 1.27). Иногда будем опускать не кривые, а только числа - номера кривых; например, на рис. 1.28 кривые нумеруются слева направо.

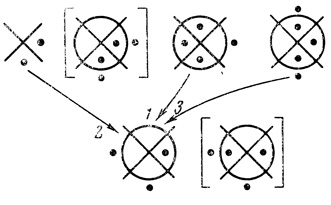
Рис. 1.25

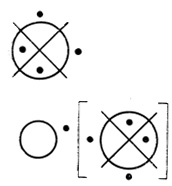
Рис. 1.26

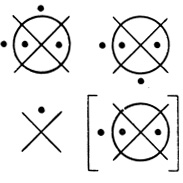
Рис. 1.27

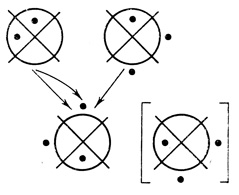
Рис. 1.28

Результирующие диаграммы^* первого ранга строятся аналогично случаю одноранговых сетей. Все они имеют n переменных, n ≥ max {n₁,.....,n_k}.

^* (Для краткости часто слова "результирующие диаграммы операторов r-того ранга" заменяем словами "результирующие диаграммы r-того ранга".)

Построение результирующей диаграммы сети. Пусть на диаграмме D^τ_2,1 в ячейках β₁,...,β_h и только в них находятся точки. Переменные оператора D^τ_2,1 обозначим через d₁ ,..., d_m где m = n_k+1 индексы 1, ..., m совпадают с номерами кривых, оканчивающихся на D^τ_2,1. Образуем диаграммы D^τ₁,...., D^τ_m если i-тая кривая начинается на диаграмме D^τ_1,j, j = 1,....,k, то D^τ_i↔[D^τ_1,j] i = 1,...,m; при этом если на диаграмме D^τ_1,j начинается t кривых, t > 1, то в указанном перечне D^τ₁,..., D^τ_m диаграмма [D^τ_1,j] повторяется t раз.

Построим символ Венна n переменных. Пусть (для определенности) ячейка β₁ есть d₁.....d_i d̄_i+1... d̄_m.

В ячейках символа Венна, совпадающих.с ячейками, в которых на всех диаграммах D^τ₁ ,...,D^τ_i находятся точки, а на всех диаграммах D^τ_i+1,....,D^τ_m нет точек, и только в них поставим по одной точке; если i = 0, то точки ставятся во всех тех ячейках, которые пусты на всех диаграммах D^τ₁,.....,D^τ_h.

Аналогично поступаем с остальными ячейками β_i оператора D^τ_2,1, 1<i≤h, при этом ранее занятые точками ячейки результирующей диаграммы (для β₁,...,β_i-1 ) не рассматриваются. Понятно, что если на операторе D^τ_2,1 нет точек, то результирующая диаграмма пуста, т. е. не содержит точек.

На рисунках результирующие диаграммы будем помещать в квадратных скобках справа от их операторов.

Пример 1.10. На рис. 1.25 дана двухранговая сеть с одним выходом, k = 3, n₁ = 2, n₂ = 3, n₃ = 3, n₄ = 3, n = 3. На выходной диаграмме D^τ_2,1 (d₁, d₂, d₃) точки расположены в ячейках 0, 3 и 4, т. е. β₁d̄₁d̄₂d₃, β₂ d̄₁d̄₂d₃, β₃ d₁d̄₂d̄₃.

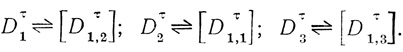
Поставим точки, соответствующие ячейке β₁ оператора D^τ_2,1. На диаграммах D^τ₁, D^τ₂, D^τ₃ только одна пустая ячейка - четвертая, поэтому на результирующей диаграмме [D^τ_2,1] в ячейке 4 ставим точку.

Перейдем к ячейке β₂ оператора D^τ_2,1.

На диаграммах D^τ₂, D^τ₃ в ячейках 0 и 3 находятся точки, а на диаграмме D^τ₁ эти ячейки пусты, поэтому в ячейках 0 и 3 диаграммы [D^τ_2,1] ставим точку; больше таких ячеек, как 0 и 3, на диаграммах D^τ₁, D^τ₂, D^τ₃ нет.

Перейдем к ячейке β₃ оператора D^τ_2,1.

На диаграмме D^τ₁ в ячейке 5 есть точка, а ячейка 5 диаграмм D^τ₂ и D^τ₃ пуста, поэтому в ячейке 5 диаграммы [D^τ_2,1] ставим точку; больше таких ячеек, как пятая, на диаграммах D^τ₁, D^τ₂ и D^τ₃ нет.

Пример 1.11. На рис. 1.28 дана двухранговая сеть с одним выходом; на операторе D^τ_2,1 (3) оканчиваются две кривые, начинающиеся на диаграмме D^τ_1,1(3), и одна кривая, начинающаяся на D^τ_1,3(3); D^τ₁ ↔ [D^τ_1,1], D^τ₂ ↔ [D^τ_1,1], D^τ₃ ↔ [D^τ_1,2].

Правила работы оператора двухранговой сети тесно связаны с операциями над диаграммами Венна.

Если оператор D^τ_2,1 имеет только две ячейки (рис. 1.1), в ячейке ā₁ (номер 0) есть точка, а в ячейке а₁ (номер 1) нет точки, то его результирующая диаграмма совпадает с отрицанием результирующей диаграммы первого ранга. В этом случае оператор будем называть оператором отрицания. Например на рис. 1.26 приведен оператор отрицания диаграммы Венна трех переменных.

Если оператор D^τ_2,1 есть диаграмма m переменных, содержащая точку только в ячейке номер 2^m - 1, то его результирующая диаграмма совпадает с конъюнкцией результирующих диаграмм первого ранга, с которыми связан этот оператор. В этом случае оператор будем называть оператором конъюнкции. Например, на рис. 1.27 содержится оператор конъюнкции двух переменных (для сравнения см. пример 1.4).

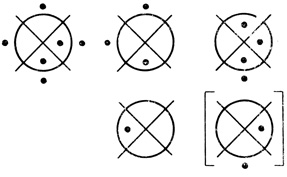
Рис. 1.29

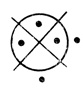
Рис. 1.30

Если оператор D^τ_2,1 есть диаграмма m переменных, m > 1, содержащая только одну точку, например в ячейке d₁... d_l d_l+1... d_m, то результат работы этого оператора совпадает с диаграммой (...((... (D^τ₁&D^τ₂)&...&D^τ_i)& D^τ_i+1)& ... & D^τ_m). Например, на рис. 1.29 дана двухранговая сеть, результирующая диаграмма которой совпадает с диаграммой ((D^τ₁ &D^τ₂)&D^τ₃), где D^τ₁ ↔ [D^τ_1,1], D^τ₂ ↔ [D^τ_1,2] и D^τ₃ ↔ [D^τ_1,3].

Действительно, диаграмма D^τ₂ есть результат операции 2 над диаграммой D^τ₂ (рис. 1.30), (D^τ₁ & D^τ₂) - результат операции 3 над D^τ₁ и D^τ₂ (рис. 1,31), ((D^τ₁&D^τ₂)&D^τ₂) - результат операции 3 над (D^τ₁&D^τ₂) и D^τ₃, графически равный результирующей диаграмме рассматриваемой сети.

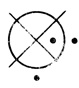
Рис. 1.31

Если оператор D^τ_2,1 есть диаграмма m переменных, содержащая h точек, h > 1, то для каждой точки отдельно можно построить диаграммы D_τ1,..., D^τ_h, тогда результат работы этого оператора совпадает с диаграммой (...(D^τ₁ ∨ D^τ₂) ∨... ∨ D^τ_h). Например, на рис. 1.32 находится двухранговая сеть, результирующая диаграмма которой совпадает с диаграммой ((((D^τ₁ & D^τ₂) & D^τ₃) ∨(( D^τ₁&D^τ₂)&D^τ₃)) ∨ ((D^τ₁ & D^τ₂) & D^τ₃)), где D^τ₁, D^τ₂ и D^τ₃ - результирующие диаграммы первого ранга.

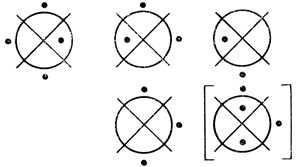
Рис. 1.32

Оператору D^τ_2,1 (m) соответствует формула Φ, составленная из переменных d₁,...., d_m, где индексы 1,..., m совпадают с номерами кривых, оканчивающихся на D^τ_2,1. i-той кривой соответствует диаграмма D^τ_i, i = 1,..., m, если кривая начинается на диаграмме D^τ_1,j, j = 1,..., k, то D^τ_i ↔ [D^τ_1,j]. Диаграмме D] соответствует формула Φ_i, составленная из n графически различных переменных, i = 1,....., m.

Пусть а₁,..., а_n - все графически различные переменные формул Φ₁,..., Φ_m. Пусть формула Ψ, составленная из n переменных а₁,...,а_n, соответствует результирующей диаграмме [D^τ_2,1] сети. Тогда формула Y есть совершенная дизъюнктивная нормальная форма формулы X, где X - результат подстановки в формулу Φ вместо переменных d₁,..., d_m соответственно формул Φ₁,..., Φ_m:

XFd1.....dmΦ1....ΦmΦ, (1.6)

Это предложение вытекает из рассмотренных правил работы оператора D^τ_2,1 двухранговой сети, связанных с операциями над диаграммами Венна в исчислении высказываний.

Пример 1.10 (продолжение). Для сети на рис. 1.25

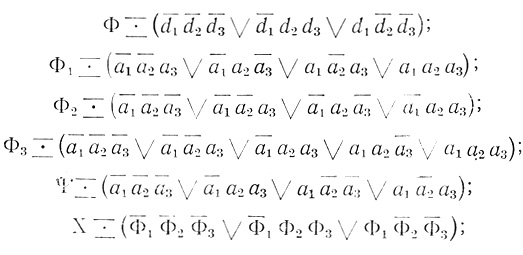
Ψ - совершенная дизъюнктивная нормальная форма формулы X.

Ясно, что без использования оператора D^τ_2,1 построение совершенной дизъюнктивной нормальной формы, составленной из переменных а₁, а₂, a³ формулы X будет более громоздким. Этот пример показывает, как сети диаграмм можно использовать для преобразования формул.

Выше (§ 1.3.) отмечалось, что по диаграмме Венна переменных а_n можно также строить формулы с меньшей логической длиной, чем их совершенная дизъюнктивная нормальная форма, в каждый дизъюнктивный член которой входят все переменные а₁...а_n (может быть с отрицанием). В случае, когда число пустых ячеек диаграммы меньше числа ячеек, занятых точками, построение удобнее начинать с пустых ячеек. Можно идти дальше, выделяя те фигуры, все ячейки которых пусты. Так, формула Φ₃, логическая длина которой равна 21, эквивалентна формуле Φ'₃ (a₁ & а₂& а₃) ∨ (а₁ & а₂)) логической длины 8; обе ячейки а₁а̄₂а̄₃ а₁а̄₂а̄₃ фигуры а₁а̄₂ на диаграмме D^τ_1,3 (рис. 1.25) пусты.

Аналогично при построении формул по ячейкам, занятым точками, можно выделять те фигуры, в каждой ячейке которых находятся точки, при этом получится ДНФ. Так, формула Φ₂ логической длины 19 эквивалентна формуле Φ'₂ ⋅ а₁ логической длины 1; ячейки ā₁ā₂ā₃, а̄₁а̄₂a₃, ā₁a₂ā₃ и ā₁a₂a₃ фигуры ах на диаграмме [D^τ_1,1] (или ячейки ā₁ā₂ и а̄₁а₂ фигуры ах на диаграмме D^τ_1,1) заполнены точками. Формула Ψ эквивалентна формуле Ψ' (а₂ & a₃) ∨ (a₁& a₂ & a₃) ∨ (a₁ & а₂)) с меньшей логической длиной.

Формула X, составленная из переменных а₁, а₂, а₃ и определяемая сетью на рис. 1.25, является избыточной по сравнению с формулой Ψ (и еще более по сравнению с формулой Ψ'), составленной из тех же переменных а₁, а₂ и а₃ и определяемой результирующей диаграммой этой сети.

Пример 1.11 (продолжение). Для сети на рис. 1.28

Φ₁Φ₂(a₁ā₂a₃∨a₁a₂a₃), Φ₁ ≡ Φ'₁

Φ'₁(а₁&а₃) (все ячейки фигуры а₁а₃ на D^τ_1,1 содержат точки);

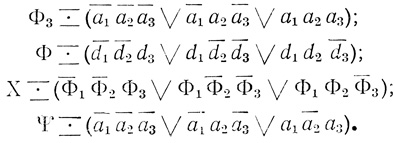
Формула X, составленная из переменных a₁, а₂ и а₃ и определяемая сетью на рис. 1.28, является избыточной по сравнению с формулой Ψ, составленной из тех же переменных а₁, а₂ и а₃ и определяемой результирующей диаграммой этой сети.

Каждой диаграмме Венна n переменных можно поставить в соответствие несколько эквивалентных между собой формул исчисления высказываний. Диаграмму можно считать результирующей диаграммой некоторой двухранговой сети с одним выходом. В этом случае число графически различных, но эквивалентных между собой формул, представляющих данную диаграмму, резко возрастает.

Совершенной дизъюнктивной нормальной формулой (СДНФ) диаграммы Венна n переменных будем называть совершенную дизъюнктивную нормальную формулу, соответствующую этой диаграмме, в каждый член которой входят все переменные а₁,...,а_n (может быть с отрицанием).

Число всех различных диаграмм Венна n переменных равно 2²ⁿ. Следовательно, один символ Венна n переменных может выражать 22" неэквивалентных между собой формул - СДНФ различных диаграмм Венна n переменных.

В двухранговой сети с одним выходом содержится k +1 символов Венна соответственно n₁, n₂,..., n_k, n_k+1 переменных. Поэтому число всех возможных случаев расположения точек на этих символах Венна, т. е. число графически различных сетей, равно

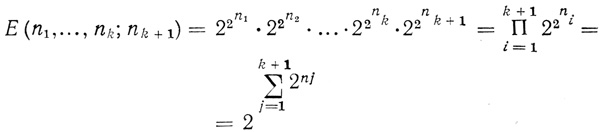(1.7)

(при этом порядок расположения кривых не учитывается).

Если n₁ = n₂ = ... = n_k = n_k+1 - n, то (1.7) преобразуется

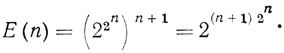(1.8)

Так как информацию, которую несет любая двухранговая сеть с одним выходом, можно выразить с помощью только одной диаграммы - результирующей диаграммы сети, то среди всех Е(n₁,... ..., n_k, n_k+1) графически различных сетей много эквивалентных.

Две сети называем эквивалентными, если их результирующие диаграммы, построенные из одних и тех же переменных, графически совпадают.

Две сети эквивалентны тогда и только тогда, когда формулы их результирующих диаграмм эквивалентны.

Обозначим число неэквивалентных между собой двухранговых сетей с одним выходом через F(n₁,..., n_k, n_k+1).

Если n₁ = n₂ = ...= n_k+1 = n, то вместо F(n₁,..., n_k, n_k+1) аналогично (1.8) пишем F(n):

- числу всех различных диаграмм Венна n переменных.

Логической избыточностью для двухранговых сетей с одним выходом будем называть отношение общего числа всех возможных графически различных сетей к общему числу всех попарно неэквивалентных сетей.

Обозначать логическую избыточность будем R₂(n₁,...., n_k; n_k+1);

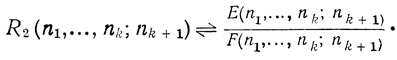(1.10)

В случае (1.8), (1.9)

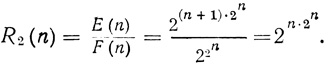(1.11)

Таким образом, сеть позволяет говорить о логической избыточности диаграмм, являющихся результатом работы сети.

Рис. 1.33

Например, для n = 1, E(n) = 16, F(n) = 4, R₂(n) = 4; на рис. 1.33 приведены все графически различные диаграммы, а на рис. 1.34 - все 16 возможных сетей для этого случая.

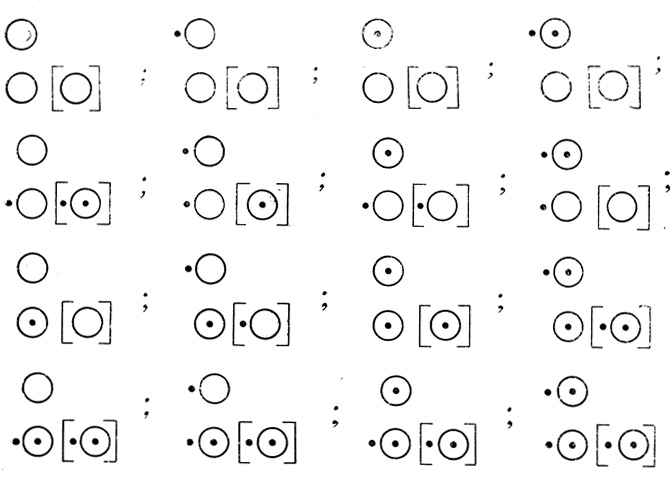
Рис. 1.34

Двухранговые сети с несколькими выходами. По построению и функционированию двухранговые сети с несколькими выходами ничем не отличаются от двухранговых сетей с одним выходом. Результирующие диаграммы операторов второго ранга строятся независимо друг от друга.

Число диаграмм в первом ранге обозначим k₁ во втором - k₂. Число переменных i-той диаграммы первого ранга обозначим n_i, i = 1,..., k₁ число переменных j-той диаграммы второго ранга - n_j, j = k₁ + 1,....., k₁+k₂ Переменные оператора D^τ_2,u, u = 1,.....,k₂ обозначим d_u,1,...,d_u,nj, где индексы 1,..., n_j совпадают сномерами кривых, оканчивающихся на D^τ_2,u, j_τ = k_τ + 1,...,k₁ + k₂.

Для каждого оператора D^τ_2,u образуем диаграммы [D^τ]_u,1, [D^τ]_u,nj: если v-тая кривая начинается на диаграмме D^τ_1,w w = 1,..., k₁, то [D^τ]_u,v ↔ [D^τ_1,w], v = 1,..., n_j.

Формулу, соответствующую оператору D^τ_2,u(n_j), фбозначим Φ_2,u. Формула Φ_2,u есть формула, составленная из переменных d_u,1 ,....,d_u,nj.

Формулу, соответствующую диаграмме [D^τ]_u,v, обозначим Φ₂, Формулу, соответствующую результирующей диаграмме [D^τ_2,u], обозначим Ψ_2,u.

Аналогично случаю двухранговых сетей с одним выходом формула Ψ_2,u и является совершенной дизъюнктивной нормальной формой формулы Х_2,u, где

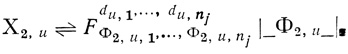(1.12)

т. е. формула Х_2,u есть результат подстановки в формулу Φ_2,u вместо переменных d_{u, 1},..., d_u,nj соответственно формул Φ_2,u,1,......,Φ_2,u,nj

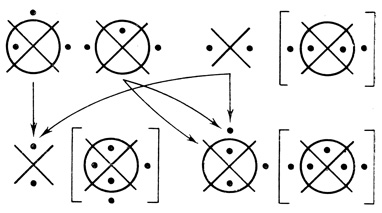
Рис. 1.35

Пример 1.12. На рис. 1.35 показана двухранговая сеть с двумя выходными диаграммами. Результирующих диаграмм две, они строятся независимо друг от друга. k₁ = 3, k₂ = 2, n₁ = 3, n₂ = 3, n₃ = 2.

Для первой выходной диаграммы D^τ_2,1(2): n₄ = 2; d_1,1, d_1,2 - переменные; [D^τ]_1,1 ↔ [D^τ_1,1], [D^τ_1,1]D^τ_1,1, [D^τ]_1,2 ↔[D^τ_1,3] точки находятся в ячейках 0 и 3;

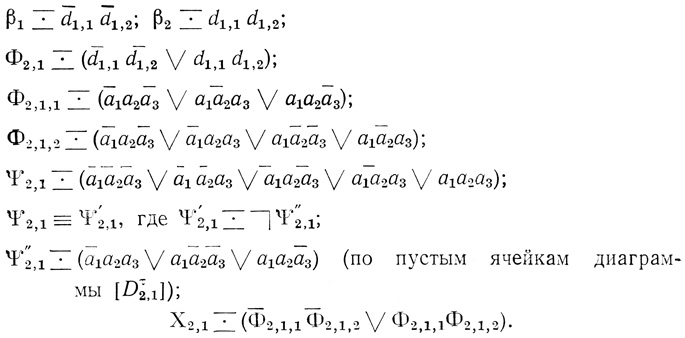
Для второй выходной диаграммы D^τ_2,2(3): n₅ = 3, d_2,1, d_2,2, d_2,3 - переменные; [D^τ]_2,1 ↔ [D^τ_1,2], [D^τ]_2,2 ↓ [D^τ_1,2], [D^τ_1,2] D^τ_1,2, [D^τ]_2,1 [D^τ]_2,2, [D^τ]_2,3 ↔ [D^τ_1,3] точки находятся в ячейках 1, 2, 6 и 7;

β₁d̄_2,1d̄_2,2d_2,3; β₂d̄_2,1d_2,2d̄_2,3' β₃d_2,1d_2,2d̄_2,3; β₄ d_2,1d_2,2d_2,3

заметим, что для ячейки (32 на диаграммах [D^τ]_2,1, [D^τ]_2,2 и [D^τ]_2,3 нет таких ячеек, в которых на [D^τ]_2,2 есть точки, а на [Dτ]_2,1 и [D^τ]_2,3 пусто, поэтому на результирующей диаграмме [D^τ_2,2] нет точек, соответствующих β₂.

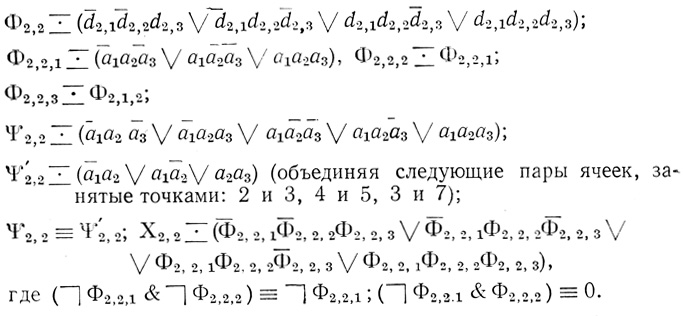
Многоранговые сети. Сети, имеющие несколько рангов, называются многоранговыми. Каждый ранг строится аналогично первому и второму рангам двухранговой сети. В первом ранге находится k₁ входных диаграмм соответственно n₁,...., n_k1 переменных, в i-том ранге k_i диаграмм соответственно n_{k1+...+ki-1+1},......., n_k1+...+ki; переменных, 1 < i ≤ g, где g - число рангов в сети.

Диаграммы g-ого ранга называются выходными.

На каждой из диаграмм n_i переменных, i ≥ k₁+1, оканчиваются стрелками n_i кривых, соединяющих эту диаграмму с некоторыми из диаграмм вышестоящих рангов.

Нумерация кривых, оканчивающихся на данной диаграмме, аналогична нумерации в двухранговых сетях. Кривые, оканчивающиеся на диаграммах, а иногда только их нумерацию, можно опустить аналогично случаю двухранговых сетей.

Построение результирующих диаграмм ведется последовательно: строятся результирующие диаграммы в первом ранге; потом - результирующие диаграммы во втором ранге, при этом диаграммы второго ранга играют роль операторов над связанными с ними результирующими диаграммами первого ранга; затем - результирующие диаграммы в третьем ранге, при этом диаграммы третьего ранга играют роль операторов над связанными с ними результирующими диаграммами в первом и во втором рангах, и т. д.; наконец, строятся результирующие диаграммы в g-том ранге, при этом выходные диаграммы играют роль операторов над связанными с ними результирующими диаграммами в вышестоящих рангах.

Результирующие диаграммы последнего ранга являются результирующими диаграммами сети.

Правила работы операторов в i-том ранге, 3 ≤ i ≤ g, ничем не отличаются от правил работы операторов в одноранговых и двухранговых сетях.

Обозначения переменных операторов и формул, соответствующих различным диаграммам, вводятся аналогично случаю двухранговых сетей с несколькими выходами.

Пример 1.13. На рис. 1.36 расположена трехранговая сеть с двумя выходами. k₁ = 3, k₂ = 3, k₃ = 2, n₁ = 3, n₂ = 3, n₃ = 2.

Для первой диаграммы второго ранга, т. е. для оператора D^τ_2,1 (4): n₄ = 4, d_2,1,1, d_2,1,2, d_2,1,3, d_2,1,4 переменные, [D^τ]_2,1,1↔[D^τ_1,1], [D^τ_1,1]D^τ_1,1, [D^τ]_2,1,2↔[D^τ_1,1], [D^τ]_2,1,3[D^τ]_2,1,1 (две кривые начинаются на первой диаграмме первого ранга), [D^τ]_2,1,3 ↔ [D^τ_1,2], [D^τ_1,2]D^τ_1,2, [D^τ]_2,1,4↔[D^τ_1,3], [D^τ_1,3]≡D^τ_1,3

точки находятся в ячейках 3,11 и 12;

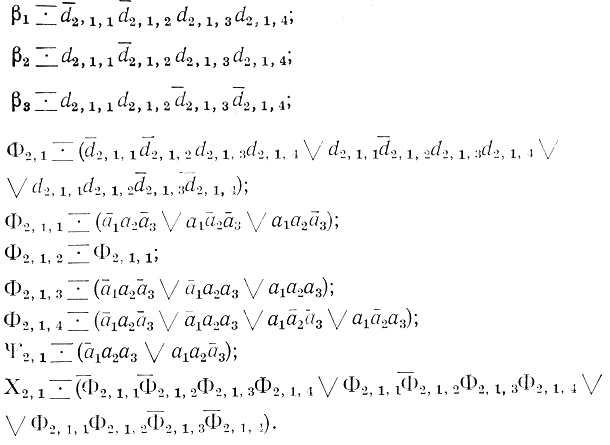
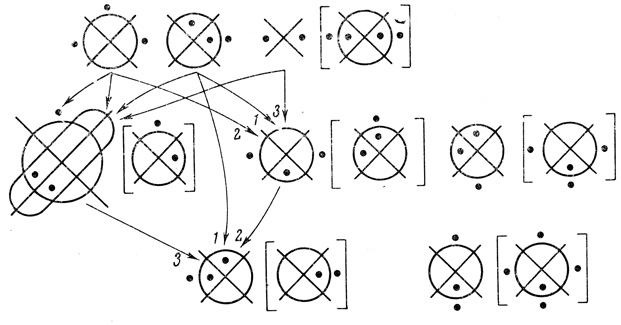
Рис. 1.36

Для второй диаграммы второго ранга, т. е. для оператора D^τ_2,2 (3): n₅ = 3; d_2,2,1, d_2,2,2, d_2,2,3 - переменные; точки находятся в ячейках 1, 2 и 4;

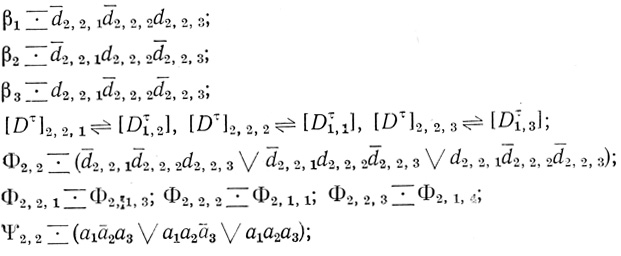
Х_2,2 (Φ̄_2,2,1Φ̄_2,2,2Φ̄_2,2,3∨Φ̄_2,2,1Φ2,2,2ΡΦ̄_2,2,3 ∨ Φ̄_2,2,1Φ̄_2,2,2Φ̄_2,2,3)

Для третьей диаграммы второго ранга D^τ_2,3(3): n₆ = 3; d_2,3,1, d_2,3,2, d_2,3,3 - переменные; [D^τ]_2,3,1 ↔ [D^τ_1,1], [D^τ]_2,3,2 ↔ [D^τ_1,2], [D^τ]_2,3,3 ↔ [D^τ_1,3] точки находятся в ячейках 0,5 и 7;

PI J_ 4, 3, l4, 3, г4, 3, з;

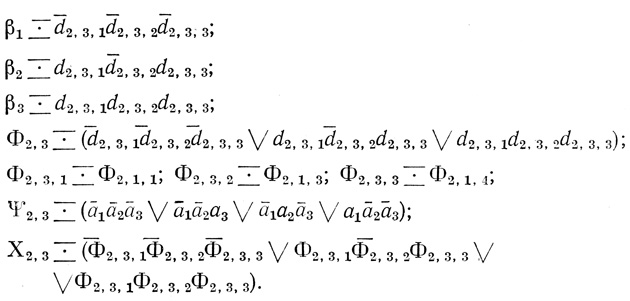
Для первой диаграммы третьего ранга D^τ_3,1(3): n₇ = 3; d_3,1,1, d_3,1,2, d_3,1,3 - переменные; [D^τ]_3,1,1 ↔ [D^τ_1,2], [D^τ]_3,1,2 ↔ [D^τ_2,2], [D^τ]_3,1,3 ↔ [D^τ_2,1]; точки находятся в ячейках 4, 5 и 7;

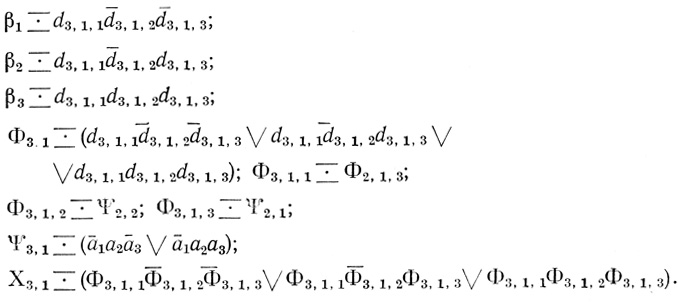
Для второй диаграммы третьего ранга D^τ_3,2(3): n₈ = 3; d_3,2,1, d_3,2,2, d_3,2,3 - переменные; [D^τ]_3,2,1 ↔ [D^τ_2,1], [D^τ]_3,2,2 ↔ [D^τ_2,2], [D^τ]_3,2,3 ↔ [D^τ_2,3]; точки находятся в ячейках 0,1 и 6;

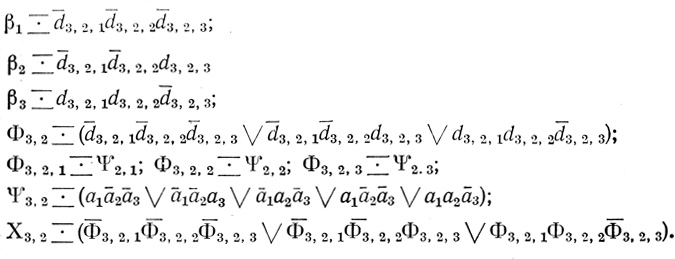
Результирующими формулами сети являются формула Ψ_3,1 - СДНФ диаграммы [D^τ_3,1] и формула Ψ_3,2 - СДНФ диаграммы [D^τ_3,2].

Формулы Х_3,1 и Х_3,2, составленные из переменных а₁, а₂ и а₃ и определяемые сетью на рис. 1.36, являются избыточными по сравнению соответственно с формулами Ψ_3,1 и Ψ_3,2, составленными из тех же переменных а₁, а₂ и а₃ и определяемыми результирующими диаграммами этой же сети.