§ 1.5. Регулярные сети диаграмм Венна

Среди сетей диаграмм выделим сети более простые по построению. Называть такие сети будем регулярными. Покажем, что для любой сети можно построить эквивалентную ей регулярную сеть.

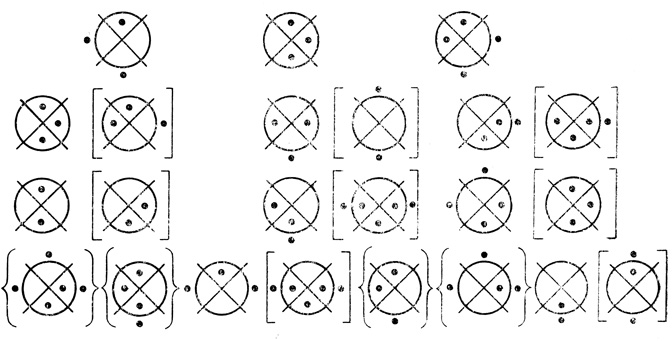
Рис. 1.37

Сеть будем называть М-регулярной, если диаграммы i-того ранга могут соединяться кривыми только с диаграммами (i - 1)-га ранга, 1 < i ≤ g, g - число рангов в сети.

Примеры М-регулярных сетей приведены на рис. 1.37, 1.38 (о диаграммах в фигурных скобках рассказывается ниже).

Очевидно, что любая двухранговая сеть является М-регулярной.

М-регулярную сеть будем называть регулярной, если она удовлетворяет следующим условиям.

1. Диаграммы первого ранга содержат одинаковое число переменных. Число переменных каждой диаграммы i-того ранга равно числу диаграмм в (i - 1)-ом ранге, 1 <i ≤ g, g - число рангов в сети.

2. На каждой диаграмме (i - 1)-го ранга может начинаться только одна кривая, оканчивающаяся на данной диаграмме i-того

ранга. Нумерация кривых, оканчивающихся на любой диаграмме t-того ранга, совпадает с нумерацией диаграмм в (i - 1)-ом ранге (слева направо), 1 < i ≤ g. В этом случае кривые на рисунках можно не чертить.

Например, сеть, показанная на рис. 1.37, регулярна, а сеть на рис. 1.38 не является регулярной.

Результирующие диаграммы первого ранга регулярных сетей совпадают с операторами первого ранга, если число переменных не увеличивается.

Обозначения для регулярных сетей:

a₁,....,a_n - различные переменные каждой диаграммы первого ранга;

k_i - число диаграмм в i-том ранге, 1 ≤ i ≤ g, g - число рангов в сети, kt равно числу переменных каждой диаграммы (i + 1)-го ранга, 1 ≤ i < g;

d_i,1,...,d_ik_i-1 различные переменные каждой диаграммы i-того ранга 1 < i ≤ g;

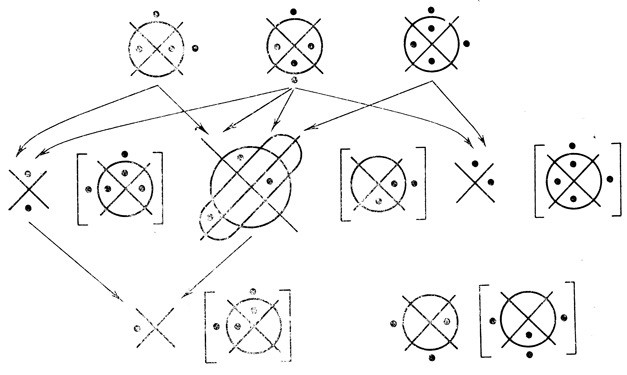
Рис. 1.38

Φ_1,1,....,Φ_1,k1 - формулы, соответствующие диаграммам первого ранга D^τ_1,1,..., D^τ_1,k1. Эти формулы составлены из переменных a₁,..., а_n и являются формулами, соответствующими результирующим диаграммам первого ранга [D^τ_1,1],..., [D^τ_1,k1]

Φ_i,1,..., Φ_i,ki - формулы, соответствующие диаграммам i-того ранга D^τ_i,1,...,D^τ_i,ki, 1 < i ≤ g. Они составлены из переменных d_i,1,......,d_i,ki-1

Ψ_i,1,.....,Ψ_i,ki - формулы, соответствующие результирующим диаграммам i-того ранга [D^τ_i,1],..., [D^τ_{i,ki1,..., аn и являются совершенными дизъюнктивными нормальными формами формул Хi,1,...,Xi,ki где}

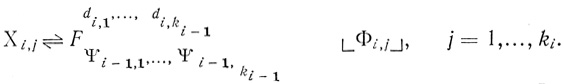(1.13)

Если i = 2,то формула Ψ_i-1,t совпадает с формулой Φ_1,t, t = 1,...,k₁.

Если i > 2, то формулы Ψ_i-1,1,...,Ψ_i-1, составленные из переменных а₁,..., а_n, являются совершенными дизъюнктивными нормальными формами формул Х_i-1,1,..., Х_i-1,ki-1, где

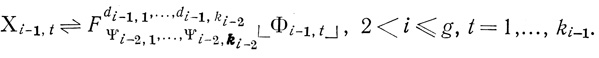(1.14)

В силу определения совершенных дизъюнктивных нормальных

формул X_i,j = X'_i,j, 2 < i ≤g, j = 1,..., k_i,

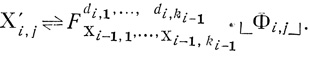(1.15)

Подставив X_i-1,t, t = 1,...., k_i-1 из (1.14) в (1.15), получим

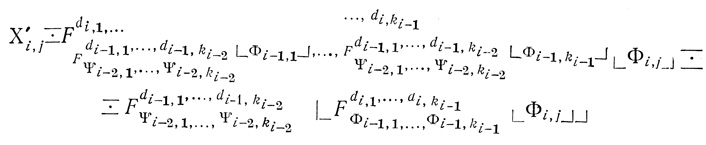(1.16)

(используется известное свойство операции подстановки: результат подстановки в некоторую формулу Φ вместо ее переменных d₁,..., d_k, формул φ₁,..., φ_k, которые в свою очередь являются результатами подстановки соответственно в формулы ψ₁,...,ψ_k, составленные из одних и тех же переменных а₁,...,a₁ вместо их переменных а₁,..., а_n формул τ₁,....., τ_n, равен результату подстановки вместо переменных а₁,...,a_n соответственно формул τ₁,..., τ_n в результат подстановки в формулу Φ вместо ее переменных d₁,..., d_k соответственно формул ψ₁,....,ψ_k).

Если i = 3, то формула Ψ_i-2,t в (1.14) - (1.16) совпадает с формулой Φ_1,t, t = 1,..., k₁.

Таким образом, результирующие диаграммы регулярных сетей с числом рангов большим чем два (g ≥ 2) можно строить не только начиная с операторов второго ранга, но и начиная с выходных операторов сети.

Во втором случае, используя (1.16), на первом шаге заменяем два последних ранга результирующими диаграммами их работы. Следовательно, на первом шаге сеть заменяется эквивалентной, но имеющей число рангов на единицу меньше, и т. д. В конце концов получаем двухранговую сеть, результирующие диаграммы которой являются результирующими диаграммами исходной сети.

На рисунках результирующие диаграммы, заменяющие два последних ранга, помещаем в фигурных скобках слева от соответствующих операторов. На втором шаге диаграммы в фигурных скобках рассматриваются как операторы над диаграммами (g - 2) -го ранга исходной сети. Если g > 3, то результирующие диаграммы этих операторов помещаем в фигурных скобках слева от соответствующих операторов. Если g = 3, то результирующие диаграммы совпадают с результирующими диаграммами исходной сети (располагаются в квадратных скобках справа от выходных диаграмм исходной сети). Общее число диаграмм, находящихся в фигурных скобках слева от выходной диаграммы сети, равно g - 2.

Формулами регулярной сети G будем называть следующие формулы X_t, t = 1,..., k_g, где k_g - число диаграмм в последнем, g-том, ранге сети G:

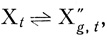(1.17)

где

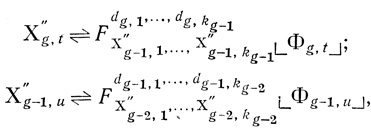
u = 1,..., k_g-1, k_g-1 - число диаграмм в (g - 1)-ом ранге сети G и т. д.;

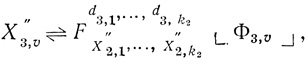
v = 1,..., k₃; k₃ - число диаграмм в третьем ранге сети G;

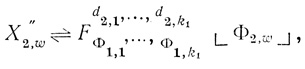
w = 1,..., k₂; k₂ - число диаграмм во втором ранге, k₁ - в первом ранге сети.

Введем также формулу X (G) ↔ (Х_⊥ & ... &X_kg).

Определим понятие избыточности относительно двух эквивалентных регулярных сетей G₁ и G₂. Будем говорить, что сеть G₁ избыточнее сети G₂, если формула X (G₁) избыточнее формулы X(G₂).

Например, четырехранговая регулярная сеть с двумя выходами (рис. 1.37) эквивалентна менее избыточной трехранговой регулярной сети (рис. 1.39), отличающейся от исходной только тем, что два последних ранга заменены их результирующими диаграммами.

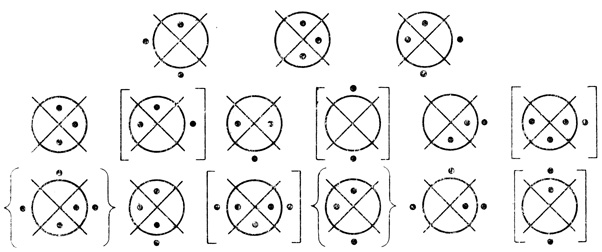
Рис. 1.39

Следовательно, описанный второй способ построения результирующих диаграмм позволяет заменить любую данную регулярную сеть эквивалентной регулярной сетью с меньшим числом рангов и поэтому являющейся менее избыточной по сравнению с исходной.

Этот процесс обратим, т. е. для любых заданных диаграмм можно построить такую регулярную сеть с любым требуемым числом рангов и с указанным количеством диаграмм в рангах, что данные диаграммы будут являться результатами ее работы. Сеть при этом строится неоднозначно. С ростом числа рангов и числа диаграмм в рангах избыточность сети увеличивается. Очевидно также, что избыточность сети увеличивается с увеличением числа точек на ее диаграммах; само собой разумеется, что речь идет о построении сетей более избыточных, но эквивалентных исходной.

Естественно, возникает вопрос о связи регулярных сетей с сетями более сложной природы (сети без обратных связей, более сложные, чем регулярные, описаны в предыдущем параграфе; о сетях с обратными связями рассказывается в следующем параграфе).

Заметим, что операцию подстановки можно проводить, начиная с последнего ранга, в любых сетях без обратных связей (необязательно регулярных). Правда, запись, похожая на (1.17), будет более громоздкой, так же как, видимо, и вопрос об обратимости этого процесса.

Покажем, что для любой сети (без обратных связей) можно построить эквивалентную ей регулярную сеть.

Начнем с М-регулярных сетей. Опишем способ построения эк-вивалентных им регулярных сетей, после чего перейдем к произвольным сетям. Укажем способ построения для любой сети (без обратных связей) эквивалентной ей М-регулярной сети. Тем самым поставленная задача о нахождении для любой сети эквивалентной ей регулярной сети будет решена.

В § 1.2 даны четыре операции над диаграммами Венна, .введем еще две операции.

5. Изменение нумерации кривых оператора. Пусть дана двух-ранговая сеть с одним выходом. Пусть β₁,...,β_h - все ячейки, в которых на D^τ_2,1 находятся точки. Пусть 1,..., m - номера кривых сети.

Построим новую двухранговую сеть с одним выходом, операторы этой сети будем обозначать D̂^τ_2,1.

Диаграммы первого ранга совпадают с результирующими диаграммами первого ранга исходной сети и имеют одно и то же число переменных. Кривые сети по расположению также совпадают с кривыми исходной сети, но нумерация их изменяется произвольным образом - число l заменяется числом l'.

Переменные D̂^τ_2,1, обозначим d'₁,....,d'_m- Каждая ячейка β на D^τ_2,1 имеет вид d̃^β₁,....,d̃^β_m, где

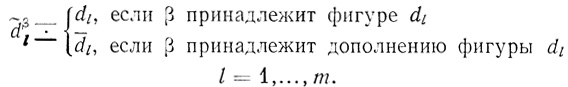
Каждой ячейке β диаграммы D^τ_2,1 поставим в соответствие ячейку β' диаграммы D̂^τ_2,1, β' ↔ d̃'^β₁ ,...,d̃'^β_m , где

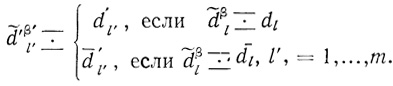
Получаем, что ячейке d₁...d_m соответствует ячейка d'₁...d'_m, а ячейке d̄₁...d̄_m - ячейка d̄'₁ ...d̄'_m.

В качестве выходной диаграммы сети возьмем оператор D̂^τ_2,1 (d'₁,...,d'_m), у которого точки находятся только в ячейках β'₁,...,β'_h соответствующих ячейкам β₁,..., β_h диаграммы D^τ_2,1.

Нетрудно убедиться, что построенная сеть эквивалентна исходной. Ее будем называть результатом операции 5 при данном изменении нумерации кривых исходной сети. В дальнейшем при применении операции 5 будем предполагать, что нумерация кривых изменяется так, что получается регулярная сеть.

Пример 1.10 (продолжение). Сеть (рис. 1.25) эквивалентна регулярной двухранговой сети с одним выходом (рис. 1.40).

6. Увеличение числа кривых оператора. Пусть дана двухранговая сеть с одним выходом. Пусть β₁,..., β_h - все ячейки, в которых на D^τ_2,1 находятся точки. Пусть 1,..., m - номера кривых сети.

Построим новую одновыходную двухранговую сеть, операторы которой будем обозначать D̄^τ_2,1.

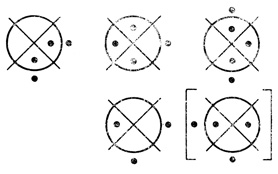
Рис. 1.40

Диаграммами первого ранга будем считать результирующие диаграммы первого ранга исходной сети и какую-то произвольную диаграмму, т. е. число диаграмм первого ранга равно k + 1, где k - число диаграмм в первом ранге исходной сети. Новая диаграмма может быть расположена в любом месте первого ранга. Будем предполагать, что все диаграммы первого ранга новой сети имеют одинаковое число переменных n, n = max (n₁,....,n_k), где n_i - число переменных на D^τ_1,i , i = 1,..., k.

Сеть имеет m + 1 кривую: m кривых по расположению и нумерации совпадают с кривыми исходной сети, (m + 1)-я кривая начинается на новой (k + 1)-й диаграмме первого ранга.

Оператором D̄;^τ_2,1 будем считать результат операции 1 над диаграммой D^τ_2,1 при увеличении числа переменных на единицу; новая переменная соответствует (m + 1)-й кривой.

Полученную сеть будем называть результатом операции 6. Нетрудно убедиться, что результат операции 6 эквивалентен исходной сети, но построенная новая сеть избыточнее исходной. Например, сеть на рис. 1.32 можно заменить эквивалентной сетью с большим числом диаграмм в первом ранге (рис. 1.41.)

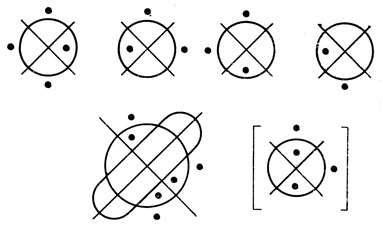
Рис. 1.41

Построение регулярных сетей, эквивалентных данной М-р егулярной сети. Дана произвольная М-регулярная сеть G. Опишем способ построения регулярной сети, эквивалентной данной.

1. Диаграммы первого ранга заменим их результирующими диаграммами с одним и тем же числом переменных n, n = max (n₁,....., n_k), где n_i - число переменных на i-той диаграмме, i = 1,.., - число диаграмм в первом ранге исходной сети. Получим сеть G₁ эквивалентную G.

2. Если на некоторой диаграмме D^τ_r,j сети G₁ начинается l кривых, l > 1, оканчивающихся на одной диаграмме D^τ_r+1,t, то в r-том ранге добавляем l - 1 диаграмму, каждая из которых отличается от D^τ_r,j только тем, что на ней начинается только одна кривая, связывающая ее с D^τ_r+1,t, при этом на D^τ_r,j из l кривых оставляем только одну; нумерация кривых, оканчивающихся на D^τ_r+1,t, не изменяется.

В результате получаем, что на каждой диаграмме r-того ранга может начинаться одна кривая из числа оканчивающихся на данной диаграмме (r + 1)-го ранга, r = 1,..., g - 1, g - число рангов в исходной сети. Построенная сеть G₂ эквивалентна G₁.

3. Увеличим число кривых, оканчивающихся на каждом операторе D^τ_r,j сети G₂, начиная со второго ранга, так, чтобы число переменных каждой диаграммы r-того ранга стало равным числу диаграмм в (r - 1)-ом ранге, 1 < r ≤ g, и чтобы на каждой диаграмме (r - 1)-го ранга начиналась только одна кривая, оканчивающаяся на рассматриваемом операторе D^τ_r,j. При этом используется операция 6, она может применяться последовательно несколько раз: при первом применении роль диаграмм первого ранга играют диаграммы (r - 1)-го ранга исходной сети, связанные с D^τ_r,j роль новой диаграммы - одна из диаграмм (r - 1)-го ранга, не связанная с D^τ_r,j.

В результате получаем, что число переменных на каждой диаграмме r-того ранга равно числу диаграмм в (r - 1)-ом ранге, на каждой диаграмме (r - 1)-го ранга начинается только одна кривая, оканчивающаяся на а число кривых, начинающихся на каждой диаграмме (r - 1)-го ранга, равно числу переменных каждой диаграммы r-того ранга. Получим сеть G₃, эквивалентную G₂.

4. Изменим нумерацию кривых, оканчивающихся на каждой, диаграмме r-того ранга сети G₃ так, чтобы она совпадала с нумерацией диаграмм в (r - 1)-ом ранге (слева направо), r = 2,..., g. При этом используется операция 5, роль диаграмм первого ранг& играют все диаграммы (r - 1)-го, а роль оператора D^τ_2,1 - диаграмма D^τ_r,j изменения при применении операции 5 могут происходить только на диаграмме D^τ_r,j.

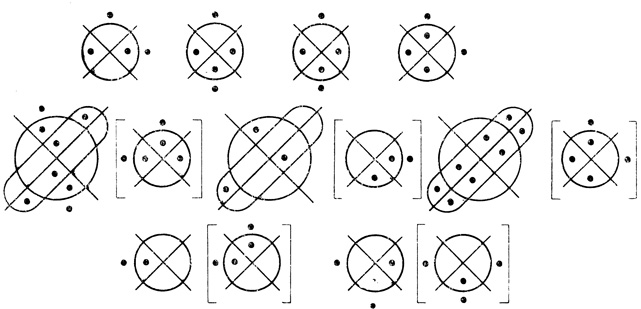
Рис. 1.42

В результате получаем регулярную сеть G₄ эквивалентную исходной сети G.

Пример 1.14. На рис. 1.42 построена регулярная сеть, эквивалентная М-регулярной сети рис. 1.38.

Построение М-регулярных сетей, эквивалентных данной. Дана произвольная сеть G. Требуется построить М-регулярную сеть, эквивалентную G.

Пусть кривая а начинается на диаграмме D^τ_r,j и оканчивается операторе D^τ_r+i,j, i > 1, 1 ≤ r < g - 1 - число рангов сети G.

Кривую α заменим последовательностью диаграмм одной переменной, в первой ячейке которых находится точка, а нулевая ячейка пуста.

К (r+1)-ому рангу добавим диаграмму D^τ_r+1,kr+1+1 одной переменной, в первой ячейке которой содержится точка, где k_r+1 - число диаграмм в (r + 1)-ом ранге. Соединим эту диаграмму кривой с диаграммой D^τ_r,t.

Аналогично добавляем диаграмму D^τ_r+u,kr+u+1 одной переменной с точкой в первой ячейке к (r + u)-ому рангу. От диаграммы D^τ_{r+u-1,kr+u-1+1} (1) К диаграмме D^τ_r+u,kr+u+1 (1) проводим кривую, u = 2,..., i - 1.

От диаграммы D^τ_r+i-1,kr+u+1 (1) проводим кривую, оканчивающуюся на диаграмме D^τ_r+i,j Этой кривой присваиваем номер кривой α сети G.

Таким способом можно заменить все кривые сети G, начинающиеся в r-том ранге и оканчивающиеся в (r + i)-ом ранге, i > 1, 1 ≤ r < g - 1. В результате получаем М-регулярную сеть G₁, эквивалентную исходной сети G. Для сети G₁ можно построить эквивалентную ей регулярную сеть G₂.

Следовательно, для любой сети можно построить эквивалентную ей регулярную сеть.

Пример 1.13 (продолжение). Трехранговая сеть G с двумя выходами (рис. 1.36) нерегулярна. На рис. 1.43 построена M-регулярная сеть, эквивалентная G.

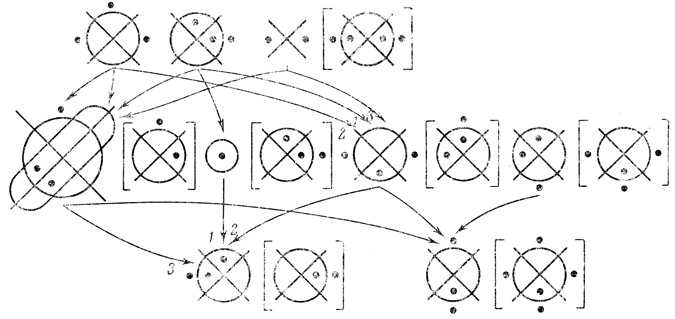
Рис. 1.43

Вернемся к соответствию между диаграммами Венна и формулами исчисления высказываний (см. § 1.3.). Покажем, что для каждой формулы Φ можно построить одновыходную сеть, результирующей диаграммой которой будет диаграмма формулы Φ.

Известно, что каждой формуле Φ, составленной из переменных a₁,...,a_n, можно поставить в соответствие дерево ее построения.

Пример 1.15. Пусть формула Φ есть ((а₂ ∨ а₃) & (а₁ ⊃ a₂))- На рис. 1.44 показано одно из деревьев ее построения, в вершинах расположены логические знаки формулы.

Дерево построения формулы Φ можно преобразовать в сеть диаграмм Венна.

Диаграммы, соответствующие переменным а₁,..., а_n, образуют первый ранг сети. Они строятся так же, как в § 1.3.

Логическому знаку отрицания соответствует оператор отрицания (см. выходную диаграмму на рис. 1.26).

Логическому знаку конъюнкции & соответствует оператор конъюнкции (см. выходную диаграмму на рис. 1.27).

Остальные логические операции можно выразить, как известно, через отрицание и конъюнкцию:

(1.18)

(1.19)

где Φ₁ и Φ₂ - произвольные формулы.

Используя (1.18), построим оператор дизъюнкции двух переменных как результирующую диаграмму сети на рис. 1.45.

Используя (1.19), построим оператор импликации как результирующую диаграмму сети на рис. 1.46.

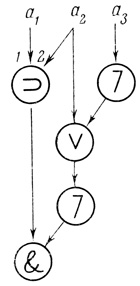
Рис. 1.44

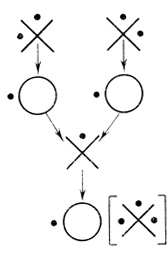
Рис. 1.45

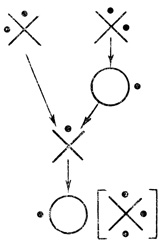
Рис. 1.46

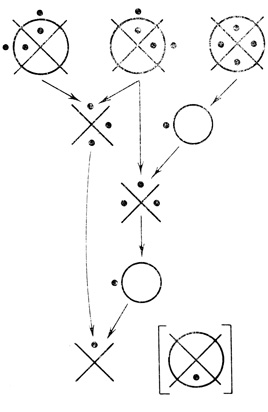
Рис. 1.47

Таким образом, сеть диаграмм G, соответствующая дереву построения формулы Φ, имеет вид: первый ранг образуют диаграммы переменных a₁,...,a_n из которых составлена формула Φ; остальные ранги получаются заменой логических знаков в дереве построения формулы на соответствующие операторы.

Построенная сеть G имеет только одну выходную диаграмму, результат ее работы является диаграммой формулы Φ. При этом сеть G, как правило, не является М-регулярной. Но можно построить эквивалентную G регулярную сеть G₁, формула X (G₁) которой является более избыточной, чем исходная формула Ф.

Пример 1.15 (продолжение). Из дерева Φ ((a₂∨a₃)&(a₁⊃a₂)) (рис. 1.44) получим сеть G диаграмм (рис. 1.47). Результат работы сети G есть диаграмма, соответствующая формуле Φ, совершенной дизъюнктивной нормальной формой которой является формула (а₁ & а₂ & а₃), построенная по результирующей диаграмме сети.