§ 1.6. Об обратных связях в сетях диаграмм Венна

Рассмотрим сети, на каждой диаграмме которых могут оканчиваться кривые, связывающие эту диаграмму с любыми диаграммами сети (в том числе и самое с собой), т. е. на каждой из диаграмм n_j переменных, начиная со второго ранга (i ≥ k₁ + 1), оканчивается стрелками n_j кривых, соединяющих эту диаграмму с некоторыми диаграммами сети, и на каждой из диаграмм первого ранга n_j переменных, 1 ≤ j ≤ k₁, могут также оканчиваться стрелками rij кривых.

В таких сетях понятие ранга не играет роли (это понятие наиболее существенно для регулярных и М-регулярных сетей), но для удобства будем им пользоваться; назовем, как и выше, диаграммы первого ранга входными, а диаграммы последнего ранга - выходными.

Будем говорить, что сеть является сетью с обратной связью, если в ней имеется по крайней мере одна диаграмма D^τ_r,j, на которой находится стрелка кривой, связывающей эту диаграмму с одной из диаграмм (r + i)-го ранга, i > 1, или с одной из диаграмм этого же, r-того, ранга.

Пример 1.16. На рис. 1.48 приведена трехранговая сеть с обратной связью: вторая кривая диаграммы D^τ_2,1 и первая кривая диаграммы D^τ_2,2 начинаются на диаграмме D^τ_3,1.

Рассматривать работу сетей будем в равноотстоящие моменты времени. Такой (временной) подход особенно удобен для сетей с обратной связью; сети без обратных связей можно исследовать независимо от времени.

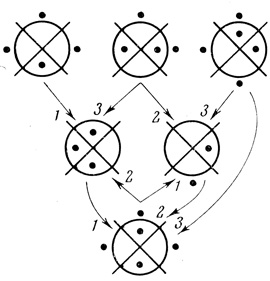
Рис. 1.48

Построение результирующих диаграмм в равноотстоящие моменты времени. Будем предполагать, что в момент времени t (начальный момент) строятся только результирующие диаграммы всех входных операторов, правила построения которых те же, что и для диаграмм первого ранга двухранговой сети; для остальных диаграмм их результирующие пусты, т. е. не содержат точек. В (t+i)-тый момент времени строятся только результирующие операторов, на которых оканчиваются стрелки кривых (в случае, когда кривые опущены, связь подразумевается).

Пример 1.13 (продолжение). Остановимся на функционировании диаграмм сети, приведенной на рис. 1.36. Рассматриваем равноотстоящие моменты времени.

В момент времени t не пусты только результирующие диаграммы первого ранга (рис. 1.49, момент t).

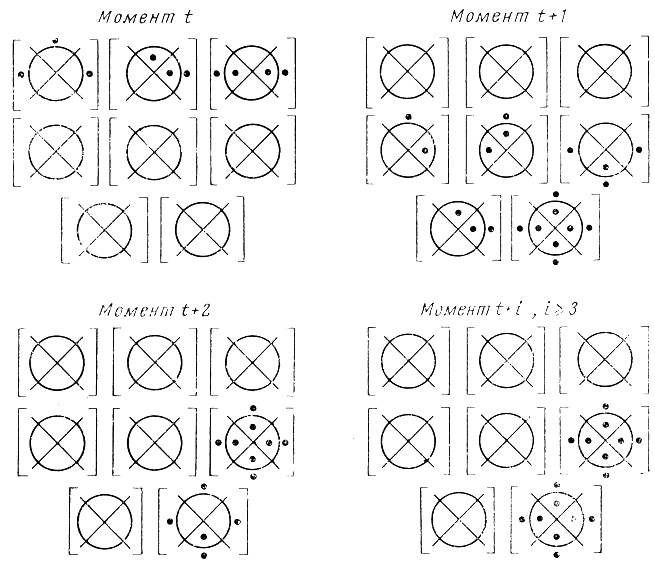
Рис. 1.49

В момент времени t + 1 пусты только результирующие диаграммы первого ранга (рис. 1.49, момент t + 1).

В моменты времени t + 2, t + 3, t + 4 и т. д. не пусты только результирующие операторов D^τ_2,3 и D^τ_3,2 (рис. 1.49, моменты t + 2, t + t, i > 2); начиная с момента времени t + 3 результирующие операторов сети повторяются.

Таким образом, ни в один из моментов времени все результирующие диаграмм сети не совпадают с результирующими диаграмм этой сети, построенными на рис. 1.36 (когда предполагалась независимость от времени).

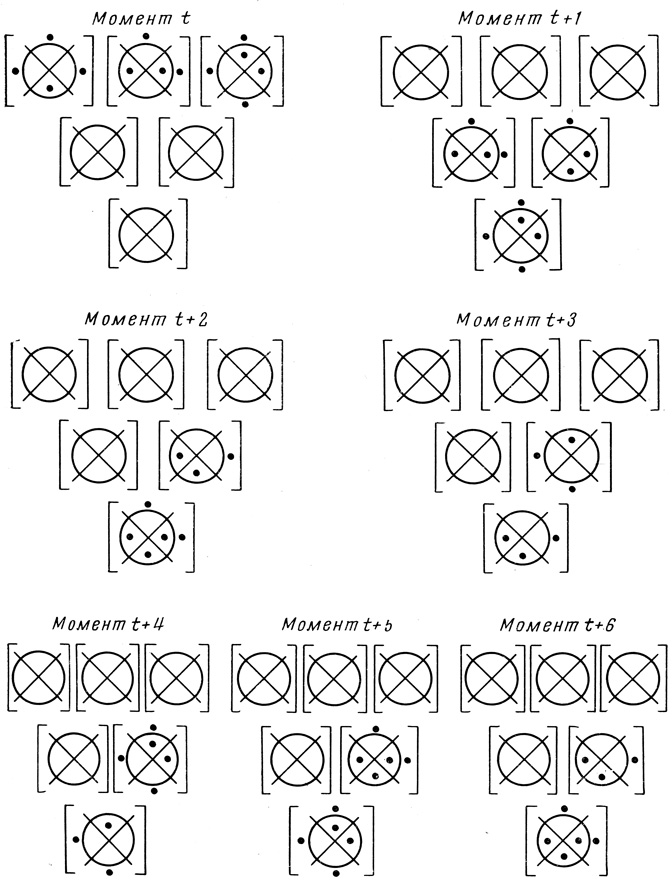
Рис. 1.50

Пример 1.16 (продолжение). На рис. 1.50 изображены результирующие диаграммы операторов сети рис. 1.48 в равностоящие моменты времени. Видим, что результирующая диаграмма сети, т. е. результат работы D^τ_3,1 не пуста, начиная с (t + 1)-го момента времени, и что результаты функционирования всех операторов сети периодически повторяются, начиная с (t +' 2)-го момента времени,- результирующие диаграммы в момент t + 2 графически совпадают с результирующими диаграммами в момент t + 6.

Определение. Будем говорить, что сеть образует временной цикл длины μ, если результирующие диаграммы всех операторов сети периодически (с периодом μ повторяются, начиная с некоторого момента времени; этот момент времени будем называть началом цикла.

В примере 1.16 момент t + 2 "является началом цикла, длина которого равна 4, μ = 4.

Временной цикл будем называть вырожденным, если, начиная с начала цикла, результаты работ всех операторов сети содержат по одной точке в каждой ячейке или являются пустыми диаграммами.

Так, например, любая М-регулярная сеть образует вырожденный цикл.

Пример 1.17. В этом примере разбирается функционирование сети (рис. 1.51), содержащей кривую, начинающуюся и оканчивающуюся на одной и той же диаграмме: вторая кривая диаграммы D^τ_2,1.

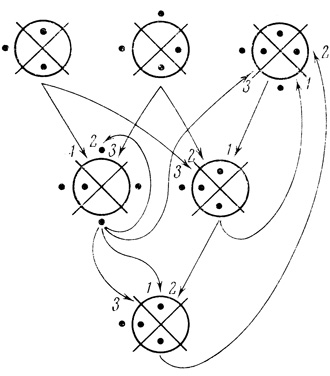
Рис. 1.51

Получается (рис. 1.52, моменты t, t + 1, t + 2, t + 3, t + i (i > 4)), что сеть образует временной цикл длины μ = 1, началом цикла является момент t + 4.

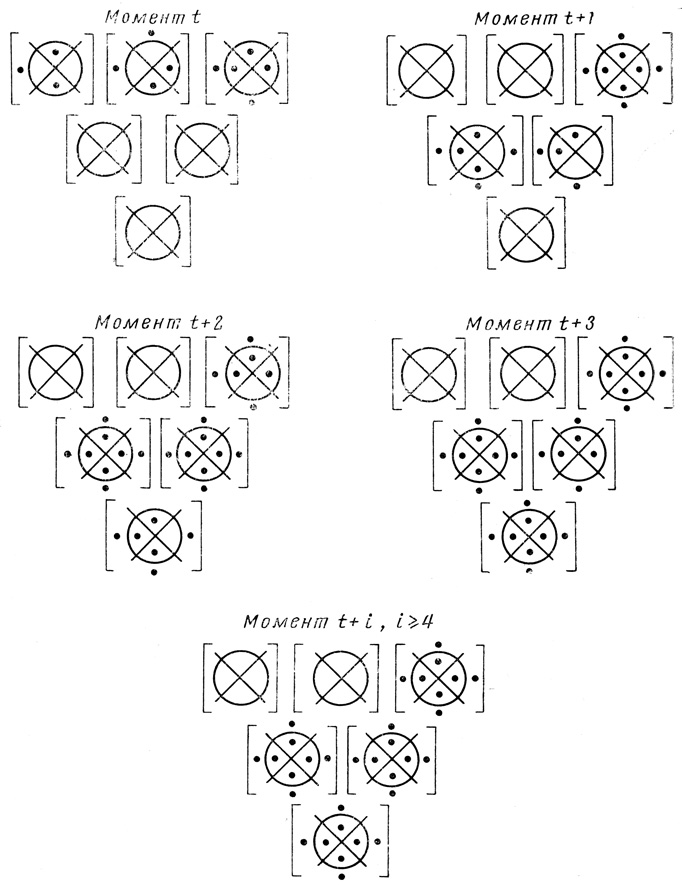
Рис. 1.52