§ 1.7. Сети вероятностных диаграмм

На сетях диаграмм Венна точки в некоторых ячейках операторов не оказывают влияния на соответствующие результирующие диаграммы.

Аналогично можно заметить, что в некоторых других ячейках (пустых) оператора можно поставить точки, не изменяя результата работы, что, конечно, ведет к увеличению избыточности сети.

Например, на диаграмме D^τ_2,1 (рис. 1.36) точку в ячейке 11 можно уничтожить, а в ячейках 4-10,14 можно поставить точки, не изменяя диаграммы [D^τ_2,1].

Из правил построения результирующих диаграмм (в том числе и для сетей с обратными связями) следует, что увеличивать или уменьшать число точек можно для операторов, начиная со второго ранга.

Если стремиться только к сохранению результирующих диаграмм сети, то число точек на операторах можно увеличивать и дальше, не обращая внимания на изменение результата работы, диаграмм, не являющихся выходными.

Каждой ячейке диаграммы Венна n переменных взаимно однозначно соответствует определенная последовательность из n единиц и нулей, которую будем называть элементарной. Среди всех 2ⁿ элементарных последовательностей, образуемых переменными оператора, можно выделить те, которые не влияют на результаты работы этого оператора. Для выделения на операторе ячеек, точки в которых не изменяют результата функционирования оператора или только выходных диаграмм сети, используются следующие вероятностные диаграммы.

Вероятностной диаграммой п переменных будем называть символ Венна n переменных, в каждой ячейке которого поставлена одна из трех букв: 1, р, 0.

На рис. 1.53 показана вероятностная диаграмма четырех переменных.

Вероятностную диаграмму n переменных будем обозначать через D^ρ, иногда указывая справа в круглых скобках число переменных или сами переменные: D^ρ (n) или D^ρ (а₁,..., а_n).

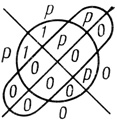
Рис. 1.53

Используя нумерацию ячеек символа Венна n переменных, вероятностную диаграмму можно записывать в линейной форме: D^ρ(n)(α₀,..., αⁿ_2-1), где α_j - одна из букв 1, ρ, 0, j = 0,..., 2ⁿ -1. Например, D^ρ (4) (0, 0, 0, 0, 0, 0, р, 0, р, 0, 1, 0, р, р, 1, р) - линейная запись вероятностной диаграммы четырех переменных на рис. 1.53.

Каждая из букв р на вероятностной диаграмме может принимать значение 1 или 0 независимо от остальных букв р на этой диаграмме.

Между вероятностными диаграммами и диаграммами Венна n переменных можно установить соответствие.

Единица в t-той ячейке вероятностной диаграммы взаимно однозначно соответствует точке в i-той ячейке диаграммы Венна.

Ноль в j-той ячейке вероятностной диаграммы обозначает, что j-тая ячейка на соответствующей диаграмме Венна пуста, и наоборот.

Буквы р вероятностной диаграммы могут принимать значения 1 или 0, независимо друг от друга, следовательно, каждой вероятностной диаграмме л переменных, в I ячейках которой находятся буквы р, соответствует 21 диаграмм Венна.

Например, вероятностной диаграмме D^ρ (3)(p, 0, 1, 1, 0, р, 0, 1) соответствуют четыре диаграммы Венна:

Из вероятностных диаграмм можно строить сети. Построение осуществляется аналогично случаю сетей диаграмм Венна, в том числе аналогично строятся М-регулярные и регулярные сети вероятностных диаграмм, а также сети с обратными связями. Единственное отличие от сетей диаграмм Венна состоит в предположении, что все входные диаграммы, содержащие по крайней мере по одной букве р, имеют одинаковое число переменных (обозначим его через n), а все остальные диаграммы первого ранга имеют число переменных, не превосходящее n.

Например, на рис. 1.54 приведена трехранговая сеть вероятностных диаграмм с двумя выходами, а на рис. 1.55 - сеть вероятностных диаграмм с обратными связями.

Будем предполагать, что все диаграммы первого ранга имеют одинаковое число переменных л.

В противном случае заменяем каждую диаграмму первого ранга D^ρ_1,i (m), m<n (без букв р) ее результирующей, содержащей n переменных. Построение результирующей диаграммы [D^ρ_1,i] осуществляется аналогично случаю одноранговых сетей диаграмм Венна (в силу установленного соответствия между вероятностными диаграммами без букв р и диаграммами Венна). Если на диаграмме D^ρ_1,i (m) оканчивается m кривых (возможно только для сетей с обратными связями), то число кривых, оканчивающихся на увеличивается до n (некоторые из кривых повторяются несколько раз; похоже на операцию 6, § 1.5).

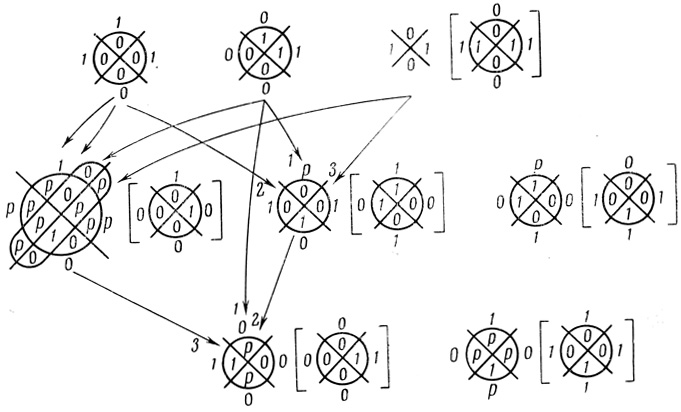
Рис. 1.54

Если на всех входных диаграммах нет букв p, то n положим равным шах (n₁,..., n_k), где n_i - число переменных на i-той диаграмме; k - число диаграмм в первом ранге; i = 1,..., k.

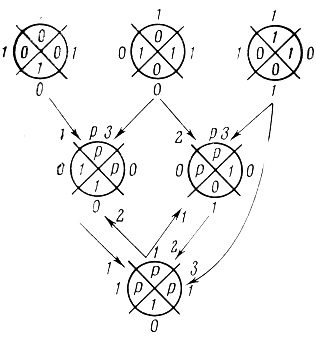
Рис. 1.55

Например, сеть на рис. 1.56 заменяем сетью на рис. 1.57.

Каждой сети вероятностных диаграмм будем ставить в соответствие одну или несколько вероятностных диаграмм n переменных а₁,...,а_n, где а₁,..., а_n - различные переменные каждой из диаграмм первого ранга. Такие диаграммы будем называть результирующими диаграммами сети. Их число совпадает с числом выходных диаграмм сети. На рисунках результирующие диаграммы помещаем в квадратных скобках справа от соответствующих выходных диаграмм.

Перейдем к построению результирующих диаграмм.

Способ 1.Перебор всех сетей диаграмм Вен-на, соответствующих данной сети вероятностных диаграмм. Пусть дана сеть G вероятностных диаграмм без обратных связей с одним выходом. Пусть I - число всех букв р на диаграммах сети G.

Тогда число сетей диаграмм Венна, соответствующих данной сети G, равно 27.

Пример 1.18. На рис. 1.59 приведены все 8 сетей диаграмм Венна, соответствующих сети вероятностных диаграмм на рис. 1.58,

Для каждой из 27 сетей диаграмм Венна можно построить соответствующую результирующую диаграмму n переменных, n - число различных переменных в первом ранге.

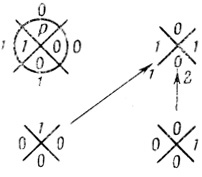
Рис. 1.56

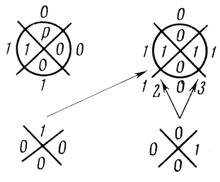
Рис. 1.57

Предположим, что все 27 результирующие диаграммы Венна построены; обозначим их D^τ₁,..., D^τ_2^I. Тогда результирующая вероятностная диаграмма исходной сети G такова:

возьмем символ Венна n переменных;

если в ячейках s₁,.....,s_k на каждой из диаграмм D^τ₁,.....,D^τ_2^I есть точки, то в соответствующих ячейках s₁,..., s_k символа Венна поставим единицы;

если ячейки i₁,.....,i_r на каждой из диаграмм D^τ₁,......,D^τ_2^I пусты, то в соответствующих ячейках i₁,...,i_r символа Венна поставим нули;

в каждой из остальных ячеек символа Венна поставим буквы р.

В полученной результирующей диаграмме сети G буква р стоит в тех и только тех ячейках, которые пусты, по крайней мере на одной из диаграмм D^τ₁,..., D^τ_2^I, и в которых на некоторых из них обязательно есть точки.

Пример 1.17 (продолжение). Вернемся к рис. 1.59. В ячейке 3 на всех результирующих диаграммах D^τ₁, ..., D^τ₈ есть точки, поэтому в ячейке 3 на результирующей диаграмме сети (рис. 1.58) находится единица. Ячейки 6 и 7 пусты на всех диаграммах D^τ₁ ,...,D^τ₈, поэтому в них на рис. 1.58 стоят нули. Для всех остальных ячеек имеются диаграмма D^τ_i, на которой эта ячейка пуста, и диаграмма D^τ_j, на которой в этой ячейке есть точка, поэтому в них на результирующей диаграмме сети (рис. 1.58) расположены буквы р.

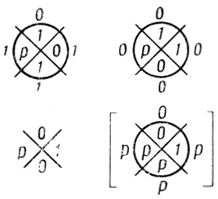
Рис. 1.58

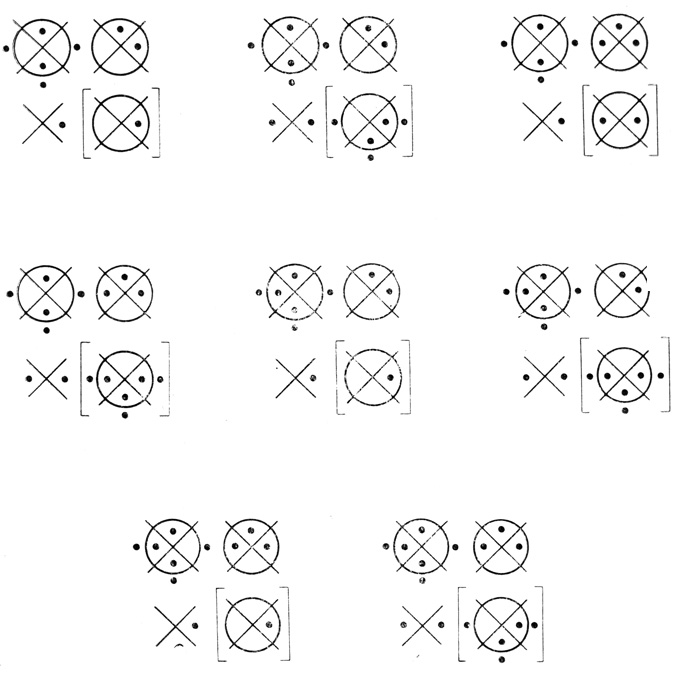
Рис. 1.59

Следует обратить внимание на то, что не любая комбинация значений букв р на результирующей вероятностной диаграмме дает некоторую из диаграмм D^τ₁ ,..., D^τ_2^I. Так, на рис. 1.59 всего четыре различных результирующих диаграммы, а букв р на результирующей диаграмме сети рис. 1.58 - пять.

Если дана сеть G вероятностных диаграмм без обратных связей с несколькими выходами, то результирующие диаграммы для каждого выхода можно строить независимо от остальных выходов. Для этого вместо сети G рассматривается l сетей G₁, ....., G_l с одним выходом, где l - число выходных операторов сети G; все ранги сети G, (i = 1,..., l), кроме последнего, совпадают с соответствующими рангами сети G, а в последнем ранге находится только i-тая выходная диаграмма сети G.

Пример 1.19. На рис. 1.54 содержится трехранговая сеть вероятностных диаграмм с двумя выходами: l = 2, I = 13 для сети G₁, I = 15 для сети G₂. Результирующие диаграммы сети не содержат букв р, им соответствуют результирующие диаграммы Венна в примере 1.13.

Остановимся на функционировании сетей вероятностных диаграмм во времени, особенно обращая внимание на сети с обратными связями.

Каждой сети вероятностных диаграмм G (G может быть сетью с обратной связью) соответствует 2^I сетей диаграмм Венна, где I - число всех букв р на диаграммах сети G. Если G - сеть с несколькими (l) выходами, то и каждая из 2^I сетей диаграмм Венна имеет I выходов.

В каждый данный момент времени t + i, i > 0, для каждой из 21 сетей диаграмм Венна можно построить свою результирующую диаграмму (см. § 1.6). Перебирая все 21 сетей диаграмм Венна в момент времени t + i, можно сконструировать результирующие вероятностные диаграммы исходной сети G в момент времени t + i аналогично случаю сетей вероятностных диаграмм без обратных связей, независящих от времени.

Пример 1.20. На рис. 1.55 приведена одновыходная сеть вероятностных диаграмм с обратной связью. Результирующие вероятностные диаграммы сети в различные моменты времени t + i, i ≥ 0, не содержат букв р, им соответствуют результирующие диаграммы Венна сети в примере 1.16.

Для построения результирующей диаграммы сети вероятностных диаграмм мы использовали 2^I сетей диаграмм Венна. Нетрудно убедиться, что среди этих 2^I сетей диаграмм Венна встречаются попарно эквивалентные между собой. Например, сети диаграмм Венна на рис. 1.59 можно разбить на четыре группы, внутри каждой из которых все сети попарно эквивалентны.

Следовательно, при нахождении результирующей вероятностной диаграммы часто можно не перебирать все 2^I сетей диаграмм Венна. Так, в примере 1.18 (рис. 1.58 и 1.59) можно ограничиться только четырьмя попарно неэквивалентными сетями диаграмм Венна.

Для каждой ячейки первого ранга буква в ячейке с тем же номером на результирующей вероятностной диаграмме определяется независимо от букв в остальных ячейках первого ранга, а каждая буква любого оператора, начиная со второго ранга, на сети диаграмм Венна функционирует независимо от остальных букв. Поэтому при конструировании результирующей вероятностной диаграммы можно ограничиться рассмотрением только тех сетей диаграмм Венна, которые получаются, когда все буквы р на каждой вероятностной диаграмме исходной сети принимают одинаковые значения. Обозначив за J количество вероятностных диаграмм данной сети, содержащих буквы р, получим, что при определении результирующей вероятностной диаграммы достаточно перебрать 2^J соответствующих сетей диаграмм Венна. В примере 1.18 J = 3, т. е. 2^J = = 27, в примере 1.19 J = 4, а I = 15 для сети С₂.

Способ 2. Перебор элементарных последовательностей n переменных. Пусть G - любая сеть вероятностных диаграмм (G может быть сетью с обратной связью и с несколькими выходами), n - число различных переменных на каждой из диаграмм первого ранга.

Если G - сеть с обратной связью, то ее поведение исследуется в фиксированные моменты времени t + i, i ≥ 0. Если G - сеть без обратных связей, то ее функционирование можно изучать как независимо от времени, так и в зависимости от момента времени, в последнем случае сеть работает аналогично сетям с обратными связями (для сравнения см. § 1.6.).

При рассмотрении сетей, зависящих от времени, основную роль играют связи между диаграммами; на чертежах эти связи выражаются с помощью кривых (иногда кривые можно опускать, тогда они подразумеваются). В момент времени t + i функционируют только те операторы сети, на которых оканчиваются стрелки кривых. Все остальные операторы сети можно считать пустыми - результатами их работы также являются пустые диаграммы (аналогично см. § 1.6). В момент времени t - начальный момент - функционируют только операторы первого ранга - входные диаграммы, а все остальные операторы можно предполагать пустыми.

Таким образом, в каждый данный момент времени t + i, i≥0, вместо сети G можно рассматривать некоторую другую сеть G_i, отличающуюся от G только тем, что некоторые диаграммы сети G воспринимаются как пустые. Поэтому при изложении второго способа построения результирующих диаграмм не будем специально выделять случай, когда работа сети зависит от времени. Само собой разумеется, что в каждом конкретном примере должно быть указано, зависит результирующая диаграмма от времени или нет (это касается только сетей без обратных связей, сети с обратными связями обязательно зависят от времени). Если предполагается зависимость от времени, то в каждый данный момент t + i сеть G заменяется сетью G_i i ≥ 0 (G0 - сеть в начальный момент времени t).

Каждой ячейке на диаграммах первого ранга соответствует определенная последовательность s_l из букв 1, р и 0 (l - номер этой ячейки), l = 0,..., 2ⁿ - 1, s_l δ_1,l,..., δ_k,l, где k - число диаграмм в первом ранге, δ_i,l есть 1,0 или р в зависимости от того, какая из букв 1, 0, р стоит в l-той ячейке на i-той диаграмме первого ранга, i = 1,..., k.

Если среди δ_1,l,..., δ_k,l нет букв р, то s_l есть элементарная последовательность. Если среди δ_1,l,..., δ_k,l встречается r букв р, то, придавая р значение 1 или 0, получим 2^r различных элементарных последовательностей.

Для каждой последовательности s_l в случае регулярных сетей можно проследить, переходя от диаграмм j-того ранга к диаграммам (j + 1)-го ранга, 1 - 1, ≤j≤g-1 гдe g - число рангов в сети, какое значение 1, 0 или р принимает данный выход сети G. Для сетей более сложных, чем регулярные, существенную роль при этом играют связи между диаграммами.

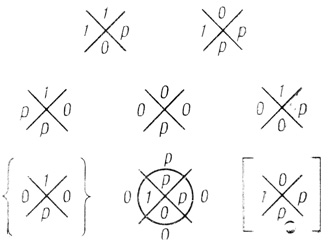
Рис. 1.60

Пример 1.21. Построим результирующую диаграмму регулярной сети на рис. 1.60. В первом ранге находится две, во втором - три вероятностные диаграммы двух переменных, а в третьем ранге - одна выходная вероятностная диаграмма трех переменных. На каждой диаграмме есть буквы р; общее число букв р в сети I = 10. Предполагаем, что функционирование сети не зависит от времени.

1. Нулевой ячейке первого ранга соответствует последовательность s₀ 0 р. Этот случай разбивается на два подслучая: р = 1, р = 0.

1,1. p = 1, т. е. значением первой диаграммы первого ранга Di, 1 (aiy аъ) является 0: записываем D^ρ_1,1 (0, 0) = 0; значением

второй диаграммы первого ранга D^ρ_1,2 (а₁, а₂) является 1: D^ρ_1,2 (0, 0)= 1, при этом а₁, а₂ - переменные первого ранга. Значения диаграмм первого ранга образуют элементарную последовательность 01, поэтому переходим к ячейке 1 (01 есть 1 в десятичной системе) диаграмм второго ранга. D^ρ_2,1 (0,1) = 0 - в ячейке 1 диаграммы D^ρ_2,1 находится 0, D^ρ_2,2 (0,1) = 0, D^ρ_2,3 (0,1) = р. Случай 1,1 в свою очередь разбивается на два подслучая.

1, 1, 1. р = 1. Значения диаграмм второго ранга образуют элементарную последовательность 001, переходим к ячейке 1 выходной диаграммы, D^ρ_3,1 (0, 0, 1) = 0.

1, 1, 2. р = 0. Значения диаграмм второго ранга образуют последовательность 000, смотрим на нулевую ячейку диаграмм третьего ранга, D^ρ_3,1 (0, 0, 0) = 0.

1, 2. р = 0. Значения диаграмм первого ранга образуют последовательность 00, D^ρ_2,1 (0,0) = р, D^ρ_2,2 (0,0) = р, D^ρ_2,3 (0,0) = 0. Следовательно, случай 1,2 распадается на 4 подслучая.

1, 2, 1. D^ρ_2,1 (0,0) = 1, D^ρ_2,2 (0,0) = 1. Значения диаграмм второго ранга образуют последовательность 110; берем ячейку 6 диаграммы D^ρ_3,1, D^ρ_3,1(1, 1, 0) = р.

Дальше случай 1 можно не разбирать, так как независимо от остальных подслучаев в нулевой ячейке результирующей диаграммы необходимо поставить р. Это аналогично нахождению двух соответствующих сетей диаграмм Венна, в нулевой ячейке результирующих диаграмм которых на одной из них пусто, а на другой стоит точка; эти сети таковы, что в нулевой ячейке диаграмм D^ρ_1,2, D^ρ_2,1, D^ρ_2,2 на обеих находятся точки, а в ячейке 6 диаграммы D^ρ_3,1 на одной пусто, а на другой есть точка.

2. Первой ячейке первого ранга соответствует последовательность s₁ pp.

2, 1. D^ρ_1,1(0,1) = 1, D^ρ_1,2 (0,1) = 1. Переходим ко второму Рангу к ячейке 3 (11 есть 3 в десятичной системе), D^ρ_2,1(1,1) = 1, D^ρ_2,2 (1,1) = 0, D^ρ_2,3 (1,1) = 1. Смотрим ячейку 5 третьего ранга (10 1 есть 5): D^ρ_1,3(1, 0, 1) = 1.

2,2. D^ρ_1,1 (0,1) = 1, D^ρ_1,2 (0,1) = 0, D^ρ_2,1 (1,0) = р, D^ρ_2,2 (1,0) = 0, D^ρ_2,3 (1,0) = 0.

2,2,1. D^ρ_2,1 (1,0) = 1, D^ρ_3,1 (1,0,0) = 0.

Дальше случай 2 можно не разбирать, так как независимо от остальных подслучаев в первой ячейке результирующей диаграммы необходимо поставить р, D^ρ_3,1 (1, 0, 1) = 1, D^ρ_3,1 (1, 0, 0) = 0.

3. Рассмотрим ячейку 2 первого ранга; ей соответствует последовательность s₂ 11, которая является элементарной последовательностью двух переменных, D^ρ_1,1 (1,0) = 1 и D^ρ_1,2 (1,0) = 1. Следовательно, D^ρ_1,2 (1,1) = 1, D^ρ_2,2 (1,1) = 0 и D^ρ_2,3 (1,1) = 1. Поэтому D^ρ_3,1 (1, 0, 1) = 1 (во второй ячейке результирующей диаграммы ставим 1).

4. Наконец, перейдем к ячейке 3 первого ранга s 10, D^ρ_1,1 (1,1) = 1, D^ρ_1,2 (1,1) = 0, D^ρ_2,1 (1,0) = р, D^ρ_2,2 (1,0) = 0, D^ρ_2,3 (1,0) = 0.

4.1. D^ρ_2,1 (1,0) = 1, D^ρ_3,1 (1,0,0) = 0.

4.2. D^ρ_2,1 (1,0) = 0, D^ρ_3,1 (0,0,0) = 0.

Таким образом, поставив в ячейке 3 букву 0, завершим построение результирующей диаграммы; на рис. 1.60 она расположена в квадратных скобках справа от выходной диаграммы.

Результаты вычислений приведены в табл. 1,7. В первом столбце даны номера ячеек первого ранга в двоичной системе (т. е. различные элементарные последовательности n переменных, n = 2), которые совпадают с номерами ячеек результирующей диаграммы; в следующих столбцах приведены значения диаграмм сети (числа в соответствующих ячейках диаграмм); ячейки с буквами р разбиваются на подъячейки (подстроки) - перебираются все возможные комбинации значений букв р, столбцы обозначаются парами чисел r, С (r - номер ранга, i - номер диаграммы в ранге), при этом в случае, когда в столбце выходной диаграммы получается или буква р, или 1 и 0 в разных подъячейках, соответствующих одной ячейке диаграмм первого ранга, перебор значений р можно прекратить, в ячейке результирующей диаграммы ставится р (в таблице, чтобы подчеркнуть, что не все возможные комбинации рассмотрены, проводим двойную горизонтальную черту и оставляем пустые под ячейки).

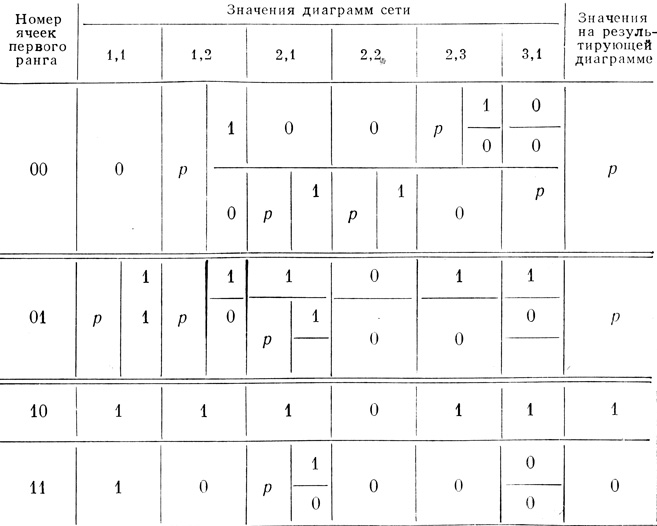
Таблица 1.7

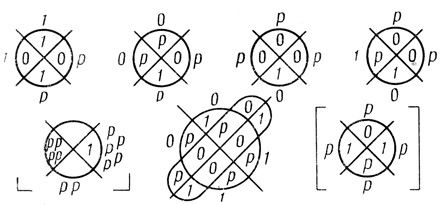
Рис. 1.61

Пример 1.22. Разберем построение результирующей диаграммы сети на рис. 1.61; она расположена в квадратных скобках справа от выходной диаграммы.

В нулевой ячейке результирующей диаграммы стоит р, так как возможны два случая: 1) D^ρ_1,1 (0, 0, 0) = 0, D^ρ_1,2 (0, 0, 0) = 0, D^ρ_1,3 (0, 0, 0) = 0 и D^ρ_1,4 (0, 0, 0) = 0, тогда D^ρ_2,1 (0, 0, 0, 0) = 1; 2) D^ρ_1,1 (0,0,0) = 1, D^ρ_1,2(0, 0,0) = 0, D^ρ_1,3 (0, 0, 0) = 0, D^ρ_1,4(0, 0, 0)= 0, тогда D^ρ_2,1 (1, 0, 0, 0) = 0.

В ячейке 1 результирующей диаграммы - р, так как D^ρ_1,1 (0, 0, 1) = D^ρ_1,2 (0, 0, 1) = D^ρ_1,3 (0, 0, 1) = D^ρ_1,4 (0, 0, 1) = 1, а D^ρ_2,1 (1, 1, 1, 1) = р.

В ячейке 2 - р, так как возможны два случая, как и для нулевой ячейки.

В ячейке 3-1: D^ρ_1,1(0, 1, 1) = D^ρ_1,2 (0, 1, 1) = D^ρ_1,3 (0, 1, 0) = D^ρ_1,4 (0, 1, 1) = 0, a D^ρ_2,1 (0, 0, 0, 0) = 1.

В ячейке 4 - p: D^ρ_1,1 (1, 0, 0) = 1, D^ρ_1,2(1, 0, 0) = 0, D^ρ_1,4(1, 0, 0) = 1, возможно D^ρ_1,3 (1, 0, 0) = 0, a D^ρ_2,1 (1, 0, 0, 1) = р.

В ячейке 5-1, так как возможны четыре случая:

1) D^ρ_1,i(1, 0, 1) = 0, i = 1, 2, 3, 4, a D^ρ_1,2(0, 0, 0, 0) = 1;

2) D^ρ_1,i (1,0,1) = 0,i = 1,2,3, D^ρ_1,4 (1, 0, 1) = 1, a D^ρ_2,1 (0, 0, 0,1) = 1;

3) D^ρ_1,i (1, 0, 1) = 0, 1 = 1, 3, 4, D^ρ_1,2 (1, 0, 1) = 1, а D^ρ_2,1(0, 1, 0, 0) = 1;

4) D^ρ_1,1(1, 0, 1) = D^ρ_1,3 (0, 0, 1) = 0, D^ρ_1,2 (1,0, 1) = D^ρ_1,4 (1, 0, 1) = 1, a D^ρ_2,1(0, 1, 0, 1) = 1.

В ячейке 6 - р: возможен случай D^ρ_1,1 (1, 1, 0) = 1 , D^ρ_1,2(1,1, 0) = 0, D^ρ_1,3(1, 1, 0) = 1, D^ρ_1,4 (1, 1, 0) = 0, a D^ρ_2,1 (1, 0, 1, 0) = p.

Наконец, в ячейке 7 - 0, так как если D^ρ_1,1( 1, 1, 1) = 1, D^ρ_1,i (1,1, 1) = 0, i = 2,3,4, то D^ρ_2,1 (1, 0, 0, 0) = 0 и если D^ρ_1,i( 1, 1, 1) = 1, i = 1,2, D^ρ_1,j( 1, 1, 1) = 0, j = 3,4, то D^ρ_2,1 (1, 1, 0,0) = 0.

Пример 1.19 (продолжение). Построение результирующих диаграмм сети (рис. 1.54) приведено в табл. 1.8. Столбцы в таблице, соответствующие значениям диаграмм сети, обозначены выражениями r, i (r₁, i₁) (r₂, i₂)... (r_k, i_k), где r - номер ранга; i - номер диаграммы D^ρ_r,i в ранге; r - номер ранга; i - номер диаграммы в r_j-том ранге, связанной с рассматриваемой диаграммой D^ρ_r,i(k) кривой с номером i, j = 1,..., k. На рис. 1.54 результирующие диаграммы находятся в квадратных скобках справа от выходных диаграмм сети.

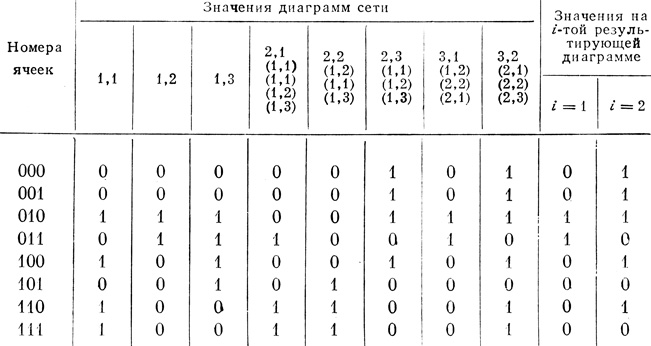
Таблица 1.8

Способ 3. Уменьшение числа рангов в регулярной сети вероятностных диаграмм. Первые два способа построения результирующих диаграмм сети связаны с перебором.

Для регулярных сетей предложим еще один метод нахождения результирующих диаграмм. Он состоит в последовательном уменьшении числа рангов, для чего два последних ранга сети заменяются вероятностными диаграммами их работы. При этом каждую выходную диаграмму сети можно рассматривать как оператор с определенными правилами функционирования.

Уменьшая число рангов, получаем новую сеть, эквивалентную исходной.

Сети G₁ и G₂ вероятностных диаграмм называем эквивалентными, если все результирующие диаграммы сети G₁ и только они являются результирующими диаграммами сети G₂ (для сравнения см. эквивалентные сети диаграмм Венна).

Уменьшать число рангов в данной регулярной сети G можно по способам 1 и 2.

Построим вероятностные диаграммы работы сети, состоящей из двух рангов - последнего и предпоследнего исходной сети G. Заменим найденными диаграммами два последних ранга сети G. Получим сеть G₁ вероятностных диаграмм, состоящую из g - 1 рангов, где g - число рангов в сети G. Сеть G₁ эквивалентна сети G. И так далее последовательно уменьшаем число рангов в сети G. В конце концов получаем одноранговую сеть, диаграммы которой являются результирующими диаграммами сети G.

На каждом шаге строятся результирующие диаграммы двухранговых сетей. Выходные диаграммы двухранговых сетей можно считать операторами, работающими над диаграммами первого ранга. Введение операторов позволяет полностью исключить перебор.

Так как результирующие диаграммы для каждого оператора строятся независимо друг от друга, то ограничимся случаем одно-выходных сетей.

Будем также предполагать, что на выходной диаграмме содержится по крайней мере одно из значений 1, р. В противном случае результирующая диаграмма имеет, как и оператор, только нули; в этом случае выходную диаграмму называем пустым оператором.

Правила работы выходного оператора регулярной двухранговой сети вероятностных диаграмм

П₀. Оператор N-переноса. Пусть выходная диаграмма D^ρ_2,1 сети G имеет только две ячейки, n_k+1 = 1. Тогда k = 1, т. е. в первом ранге находится только одна диаграмма (n).

Пусть на диаграмме D^ρ_2,1 (1) в нулевой ячейке находится 0, в первой - 1; на диаграмме (n) в ячейках β₁,..., β_l - 1, в ячейках β₁,..., β_r - р, в ячейках _r+1,..., β_2ⁿ - 0.

Построим символ Венна n переменных, в ячейках поставим буквы, графически равные буквам, лежащим в соответствующих ячейках диаграммы D^ρ_1,1(n). Получим вероятностную диаграмму [D^ρ_2,1] - результат работы данной сети G. В этом случае диаграмму D^ρ_2,1 называем оператором N-переноса, в силу построения [D^ρ_2,1][D^ρ_1,1(n)]

Π^p₀. Оператор N_p-переноса. Пусть предположения правила П₀ сохраняются, за исключением того, что в первой ячейке на D^ρ_2,1 (1) стоит не единица, а р. Диаграмму D^ρ_2,1 (1) называем оператором N_p-переноса.

Построим символ Венна n переменных, в ячейках β₁,..., β_r поставим р, в ячейках β_r+1,..., β_2ⁿ - 0. Получим вероятностную диаграмму [D^ρ_2,1] - результат работы данной сети G.

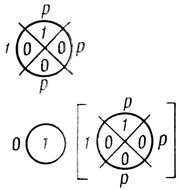
Рис. 1.62

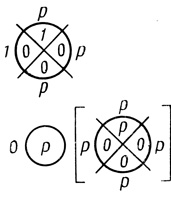
Рис. 1.63

Пример 1.23. Работа оператора N-переноса демонстрируется на рис. 1.63, а работа оператора N_р-переноса - на рис. 1.62; диаграммы первого ранга на обоих рисунках совпадают.

П₁. Оператор N-отрицания. Пусть предположения правила П₀ сохраняются, только пусть на диаграмме D^ρ_2,1 (1)в нулевой ячейке находится 1, а в первой - 0.

Такую диаграмму D^ρ_2,1(1) будем называть оператором N-отрицания.

Построим символ Венна n переменных, в ячейкам β_r+1,...,β_2ⁿ поставим 1, в ячейках β_l+1,..., β_r - р, в ячейках β₁,.. , β_l - 0. Получим вероятностную диаграмму [D^ρ_2,1], являющую результирующей диаграммой исходной сети G.

П^p₁. Оператор N_p-отрицания. Пусть предположения правила П₁ сохраняются, только в нулевой ячейке на диаграмме D^ρ_2,1 (1) стоит не единица, а буква р. В этом случае диаграмму D^ρ_2,1 (1) называем оператором N_р-отрицания.

Построим символ Венна n переменных, в ячейках β_l+1 ,...,β_2ⁿ поставим р, в ячейках β₁,..., β_l - 0. Получим вероятностную диаграмму [D^ρ_2,1], которая является результирующей диаграммой исходной сети G.

Пример 1.24. На рис. 1.64 показана работа оператора N-отрицания при n = 3. На рис. 1.65 - работа оператора N_р-отрицания при n = 4.

П₂. Оператор N-конъюнкции. Пусть рассматривается сеть G, выходная диаграмма которой имеет 4 ячейки, n_k+1 = 2. Тогда k = 2, т. е. в первом ранге сети G расположены две диаграммы: D^ρ_1,1 (n) и D^ρ_1,2 (n).

Пусть на D^ρ_2,1 (2) в ячейке 3 стоит 1, а в остальных ячейках -0, в ячейках β₁,....,β_l диаграмм D^ρ_1,1 (n) и D^ρ_1,2 (n) = 1, в ячейках β_s+1,.....,β_m-1 диаграмм D^ρ_1,1 (n) и D^ρ_1,2(n) = р, в ячейках β_s+1,.....,β_q-p на диаграмме D^ρ_1,1(n) и р на диаграмме D^ρ_1,2(n), в ячейках β_m+1,......,β_q-p на D^ρ_1,1 (n) и 1 на D^ρ_1,1 (n), во всех остальных ячейках стоит нуль, по крайней мере, на одной из диаграмм D^ρ_1,1 (n) или D^ρ_1,2 (n).

Диаграмму D^ρ_2,1 (2) будем называть оператором N-конъюнкции.

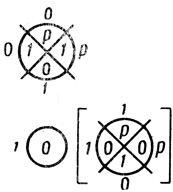
Рис. 1.64

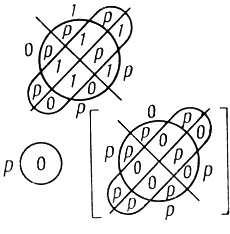
Рис. 1.65

Построим символ Венна n переменных, в ячейках β₁,..., β_l, поставим 1, в ячейках β_l+1,...., β_q - p, во всех остальных ячейках - 0.- Получим вероятностную диаграмму [D^ρ_2,1] - результат работы оператора N-конъюнкции.

П^p₂. Оператор N_p-конъюнкции. Пусть предположения правила П₂ сохраняются, только пусть в ячейке 3 диаграммы D^ρ_2,1(2) стоит не единица, а р.

Построим символ Венна n переменных, в ячейках β₁,..., β_q поставим р, во всех остальных - 0. Получим вероятностную диаграмму [D^ρ_2,1] - результат работы данной сети G. В этом случае D^ρ_2,1 (2) называем оператором N_р-конъюнкции.

Пример 1.25. На рис. 1.66 и 1.67 дана соответственно работа операторов N-конъюнкции и N_p-конъюнкции при n = 4.

П₃. Рассмотрим случай, когда на выходной диаграмме D^ρ_2,1 находится только одна отличная от нуля буква - единица. Предположим, что диаграмма D^ρ_2,1 отличается от выходных диаграмм в правилах П₀, П₁ и П₂.

Пусть эта единственная единица на D^ρ_2,1 (m) лежит в ячейке Δ d̃₁,....., d̃_m, где d₁,..., d_m - все графически различные переменные диаграммы D^ρ_2,1,

j = 1,..., m.

Для определенности пусть Δ d̄₁ ... d̄_id̄_i+1... d̄_m (0 ≤ i≤ m, i = 0 означает, что Γ d₁... d_m, i = m - Δ d̄₁... d̄_m).

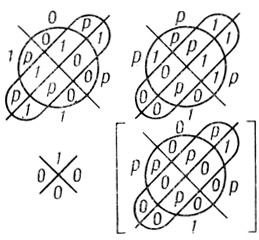
Рис. 1.66

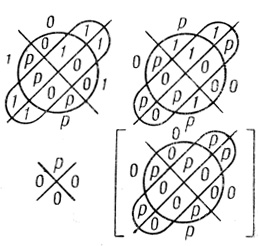
Рис. 1.67

Построим N-отрицания диаграмм D^ρ_1,1(n),..., D^ρ_1,i (n) (по правилу П₁). К полученным диаграммам [D^ρ_1,1],..., [D^ρ_1,i] и к диаграммам D^ρ_1,i+1(n),...., D^ρ_1,m(n) применим последовательно правило П₂: от диаграмм [D^ρ_1,1] и [D^ρ_1,2] перейдем к диаграмме D^ρ₁, от диаграмм D^ρ₁ и [D^ρ_1,3] - к диаграмме D^ρ₂ и т. д. от диаграмм D^ρ_i-1 и D^ρ_1,i+1 - к диаграмме D^ρ_i, и т. д., наконец, D^ρ_m-2 и D^ρ_1,m к диаграмме D^ρ_m-1, являющейся результирующей диаграммой работы исходной сети.

Правило П₃ можно сформулировать также следующим образом.

Перенесем на символ Венна результирующей диаграммы, во-первых, те и только те единицы, для которых соответствующие ячейки на всех диаграммах D^ρ_1,1,..., D^ρ_1,i пусты, а ячейки на всех диаграммах D^ρ_1,i+1,..., D^ρ_1,m заполнены единицами, во-вторых, те и только те нули, для которых в соответствующих ячейках, по крайней мере на одной из диаграмм D^ρ_1,1,..., D^ρ_1,i, стоит единица или, по крайней мере на одной из диаграмм D^ρ_1,i+1,..., D^ρ_1,m - нуль.

Во всех остальных ячейках символа Венна результирующей диаграммы (не заполненных нулями и единицами) расположим по одной букве р.

Правило П₃ является обобщением правил П₀, П₁ и П₂. Поэтому, говоря об этом правиле, в дальнейшем предполагаем, что П₀, П₁ и П₂ - частные случаи П₃.

П^p₃. Правило П₃ отличается от П₃ только тем, что на диаграмме D^ρ_2,1 единица заменена на р, а вместо правила П₂ применяется правило П₂.

Правило П₃ короче формулируется так.

Перенести на символ Венна результирующей диаграммы те И только те нули, для которых в соответствующих ячейках, по крайней мере на одной из диаграмм D^ρ_1,1,..., D^ρ_1,i, находится единица или на одной из диаграмм D^ρ_1,i+1,..., D^ρ_1,m - нуль; во всех остальных ячейках символа Венна поставить буквы р.

Аналогично П₃ правило П₃ является обобщением правил П^p₀, П^p₁ и П^p₂.

Пример 1.26. Возьмем регулярную сеть вероятностных диаграмм на рис. 1.68. Она имеет два выхода. Первый (слева) выходной оператор действует по правилу П₃, второй - по правилу П^p₃.

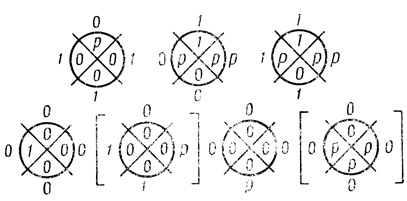
Рис. 1.68

П₄. Оператор N-дизъюнкции. Пусть на D^ρ_2,1 (m) находится s, s > 1, отличных от нуля букв 1, р: Δ₁,..., Δ_r,.,...,Δ_s, где Δ_i 1, i = 1, .., r, r > 0; Δ_j р, j = r + 1 s, s > r.

По правилу П₃ для Δ₂, если Δ_r 1, построим вероятностную диаграмму, не обращая внимания на буквы Δ_s, сотрем на ней все нули, получим диаграмму С₁.

По правилу П₃ для Δ₂, если Δ₂ 1, построим вероятностную диаграмму, не обращая внимания на буквы Δ₁, Δ₃,..., Δ_s, перенесем с нее все знаки 1, р в соответствующие ячейки диаграммы С₁, получим диаграмму С₂, в некоторых ячейках которой может содержаться две буквы р.

И так далее. По правилу П₃ для Δ_r, если Δ_r 1. построим вероятностную диаграмму, не обращая внимания на буквы Δ_r-1,Δ_r+1,..., Δ_s, перенесем с нее все знаки 1, р в соответствующие ячейки диаграммы С_r-1, получим диаграмму С_r.

По диаграмме С_r построим вероятностную диаграмму D^ρ_r (n).

Возьмем символ Венна n переменных. В ячейках β_j символа Венна, соответствующих пустым ячейкам диаграммы С_r, поставим 0. В ячейке β_i поставим 1, если 1 находится в ячейке β_i диаграммы С_r или если в m-членной последовательности из знаков 1,0, р, соответствующей ячейке β_i вероятностных диаграмм первого ранга, находится только t букв р, а в ячейке β, диаграммы С_r находится 2^t букв р. Пусть β₁,.....,β_u - все ячейки символа Венна, в которых постановлена одна из букв: 1 или 0. Во всех остальных ячейках поставим по одной букве р. Получим диаграмму D^ρ_r (n). Если r - 0, то будем считать, что на D^ρ_r (n) находятся только нули.

По правилу П^р₃ для Δ_r+1, если Δ_r+1p, построим вероятностную диаграмму, не обращая внимания на буквы Δ₁,..., Δ_r, Δ_r+2,..., Δ_s, перенесем с нее знаки р в соответствующие ячейки диаграммы D^ρ_r(n), не занятые 1, р (заменяя 0 на р), получим диаграмму D_r+1(n).

И так далее. По правилу П^p₃ для Δ_s, если Δ_sр, построим вероятностную диаграмму, не обращая внимания на буквы Δ₁,.....,Δ_s-1 перенесем в нее знаки р в соответствующие ячейки диаграммы Dps~1 (п), не занятые 1, р (заменяя 0 на р), получим диаграмму D^ρ_s-1 (n) - результат работы исходной сети.

В этом случае диаграмму D^ρ_2,1(m) называем оператором N-дизъюнции, а диаграмму D^ρ_s(n) - результатом функционирования оператора N-дизъюнкции.

Пример 1.22 (продолжение). Оператор D^ρ_2,1 (4) сети (рис. 1.61) содержит s = 10 отличных от нуля букв, поэтому он является оператором N-дизъюнкции. В ячейках 0, 1, 4, 5 и 14 расположены единицы, r = 5; в ячейках 2, 6, 9, 10 и 15 - буквы р, во всех остальных ячейках - нули.

Диаграмма С_r построена в угловых скобках слева от оператора.

При построении вероятностной диаграммы работы регулярной сети третий способ предпочтительнее, потому что выходная диаграмма двухранговых сетей есть оператор с указанными правилами работы. У многоранговых регулярных сетей последовательное уменьшение рангов можно вести снизу вверх, заменяя два последних ранга сети вероятностной диаграммой их работы, но нельзя вести сверху вниз - нельзя заменять первые два ранга сети результатами работы соответствующих двухранговых сетей.

Пример 1.21 (продолжение). На рис. 1.60 в фигурных скобках слева от выходной диаграммы - результат работы двух последних рангов. Рассматриваемая сеть эквивалентна двухранговой сети, первый ранг которой совпадает с первым рангом на рисунке, а второй образует диаграмма в фигурных скобках.

Пример 1.27 Трехранговая сеть на рис. 1.69 неэквивалентна сети рис. 1.70, хотя у этих сетей выходные диаграммы совпадают, а первый ранг сети на рис. 1.70 образован соответствующими результирующими диаграммами второго ранга.

Операторы, рассмотренные при третьем способе построения результирующих диаграмм сети, связаны с операциями над диаграммами Венна в исчислении высказываний не только по названию. Если ограничиться сетями вероятностных диаграмм без букв р, то оператору N-отрицания в сетях диаграмм Венна соответствует оператор отрицания, оператору N-конъюнкции - оператор конъюнкции, а результату работы оператора N-дизъюнкции соответствует s-кратное применение операции дизъюнкции (s - количество единиц на операторе N-дизъюнкции).

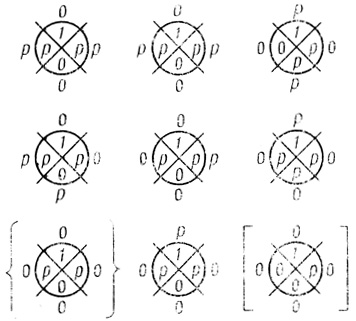
Рис. 1.69

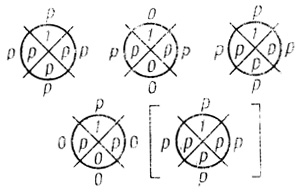
Рис. 1.70

Определения. Сеть вероятностных диаграмм называется надежной, если результирующие диаграммы сети не содержат букв р.

Сеть называется не вполне надежной, если среди ее результирующих диаграмм имеется по крайней мере одна, содержащая буквы р.

В частности, вероятностная диаграмма является не вполне надежной или надежной в зависимости от того, есть на ней буквы р или нет.

Так, сети, разобранные в примерах 1.19 (рис. 1.54) и 1.20 (рис. 1.55), являются надежными, а сети в примерах 1.21 (рис. 1.60) и 1.22 (рис. 1.61) - не вполне надежными.

Ниже сети вероятностных диаграмм будут использованы не только для описания функционирования формальных нейронов, но и при решении проблемы конструирования надежных сетей из не вполне надежных формальных нейронов (глава 4 настоящей работы). На языке вероятностных диаграмм задача построения надежных сетей из не вполне надежных элементов ставится следующим образом.

Даны надежные вероятностные диагоаммы n переменных D^ρ₁(n),...,D^ρ_k (n), k > 1.

Требуется построить надежную сеть G вероятностных диаграмм, состояющую из g рангов, g > 1, и имеющую в r-том ранге n не вполне надежных вероятностных диаграмм, содержащих максимально возможное число букв р, r = 1,....,g, так, чтобы результирующими диаграммами сети G являлись только данные вероятностные диаграммы D^ρ₁(n),..., D^ρ_k (n), не содержащие букв р.