Глава 2. Функционирование формальных нейронов и сетей из них

§ 2.1. Описание функционирования формальных нейронов диаграммами Венна в исчислении высказываний

Вернемся к формальным нейронам в смысле Мак-Каллока (§ 0.3).

В каждый данный момент времени t входы нейрона А (а₁,..., а_n) образуют определенную последовательность из n нулей и единиц, где единица на i-том месте обозначает возбужденность входа а_j, нуль на j-том месте - не возбужденность входа а_j. Эту последовательность из n нулей и единиц называем элементарной или входной последовательностью переменных а₁,..., а_n.

Каждой элементарной последовательности поставим во взаимно однозначное соответствие ячейку символа Венна n переменных. При этом будем предполагать, что номер ячейки, записанный в двоичной системе, совпадает с рассматриваемой элементарной последовательностью. Например, для n = 4 (рис. 1.9) числа, написанные в ячейках плоскости, можно воспринимать как соответствующие входные последовательности нейрона, который имеет четыре входа.

Порог θ нейрона А в момент t принимает определенное значение θ_j. Нейрон возбуждается в рассматриваемый момент времени t, если сумма возбуждающих и тормозящих единиц, соответствующих входной последовательности в момент времени t - 1 (с учетом действия всех запретов), не меньше θ_j.

Если значение порога θ фиксировано θ = θ₀, то нейрон возбуждается или не возбуждается в зависимости только от входных последовательностей.

Функционирование нейрона с n входами при фиксированном значении его порога, θ = θ₀, можно описать на языке диаграмм Венна в классическом исчислении высказываний:

если нейрон возбуждается при данной входной последовательности s, то в s-той ячейке символа Венна n переменных ставится точка;

если нейрон не возбуждается при данной входной последовательности s, то s-тая ячейка символа Венна n переменных пуста.

При изменении значения порога 0 диаграмма Венна может изменяться, и для каждого значения порога может быть вычерчена своя диаграмма Венна.

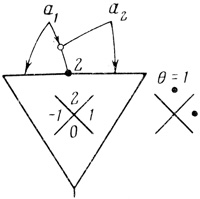
Рис. 2.1

Пример 2.1. Построим диаграммы Венна для различных значений порога нейрона, расположенного на рис. 2.1. Записывать диаграммы Венна будем в линейной форме.

Нейрон имеет два входа: а₁ и а₂, поэтому диаграммы содержат по две переменных а₁ и а₂:

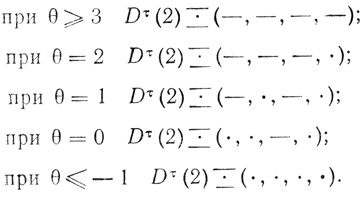
Возможны случаи, когда при изменении значения порога нейрона на единицу число точек на соответствующей диаграмме Венна не изменяется или изменяется сразу на k, k > 1. Такие нейроны называются вырожденными.

Определение. Нейрон называется невырожденным в данном интервале изменения его порога 0 в том и только в том случае, если при изменении значения его порога на единицу, не выходя за границы указанного интервала, количество точек на соответствующей диаграмме Венна изменяется также на единицу.

Заметим, что при уменьшении значения порога θ, после того как получена полная диаграмма D^τ, любой нейрон вырождается; диаграмму D^τ называем полной, если во всех ее ячейках находятся точки. Аналогично любой нейрон вырождается при увеличении значения порога 0 после того, как получена пустая, т. е. не содержащая точек, диаграмма D*.

Пример 2.1 (продолжение). Нейрон (рис. 2.1) является невырожденным в интервале α₁ ≥ θ ≥ α₂, где α₁ и α₂ - такие целые числа, что 3 ≥ α₁ ≥ α₂ ≥ - 1.

Если α₁ ≥ θ ≥ α₂, где α₁, α₂ - целые числа, то длиной интервала изменения порога θ будем называть число θ̄ ↔ α₁ - α₂.

Если θ̄ = 0, то любой нейрон будет невырожденным.

Пример 2.2. Диаграммы Венна нейрона рис. 0.1 имеют три переменных: а₁, а₂, а₃ и

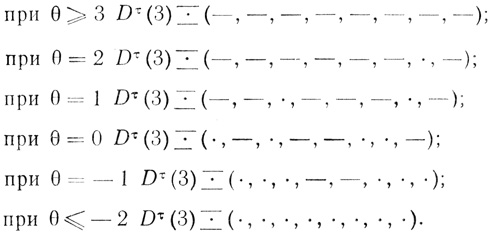
Следовательно, этот нейрон является невырожденным при θ̄ ≠ 0 тогда и только тогда, когда 3≥α₁>α₂≥1.

Сети формальных нейронов. Каждая сеть состоит из нескольких рядов (рангов) формальных нейронов. Входами сети являются все различные входы нейронов первого ранга, выходами - все выходы нейронов последнего ранга. Входами нейронов, начиная со второго ранга, могут являться только входы сети или выходы некоторых нейронов сети (возможен случай, когда выход нейрона совпадает с его входом).

Все входы каждого нейрона нумеруются числами, которые ставятся слева от них. Для однозначности иногда справа от этих чисел в круглых скобках ставим номер ранга - r и номер нейрона в ранге - i; например, 2 (5,3) - второй вход третьего нейрона в пятом ранге, r = 5, i = 3 (на рисунках ранги нумеруются сверху вниз, нейроны в рангах-слева направо). В случае, когда входы расположены линейно (слева направо) и когда не может быть их разно-чтения, числа (номера входов) будем опускать.

В настоящем параграфе ограничимся случаем, когда входами нейронов r-того ранга, r > 1, могут быть только входы сети или выходы нейронов вышестоящих рангов (вышестоящие ранги: первый,..., (r- 1)-й), а все входы первого ранга независимы (т. е. ни один из них не может совпадать с выходом некоторого нейрона сети). При этом предполагается, что функционирование нейронов сети не зависит от времени - это соответствует тому, что при пере-ходе через синапс не происходит задержки на единицу времени. Более общий случай разбирается в этой главе далее.

Одноранговые сети формальных нейронов. Каждый нейрон с n входами представляет собой одноранговую сеть с одним выходом. Для любого значения его порога θ можно построить соответствующую диаграмму Венна п переменных. Такую диаграмму будем называть квазирезультирующей диаграммой при данном значении порога θ. Квазирезультирующую диаграмму будем считать одноранговой сетью диаграмм Венна с одним выходом, результирующую диаграмму которой будем рассматривать как результирующую диаграмму исходной сети формальных нейронов при данном значении порога θ.

Квазирезультирующую диаграмму нейрона помещаем справа - от нейрона или на теле нейрона, указывая значение порога θ, при котором она получена.

Например, на рис. 2.1 справа От нейрона - квазирезультирущая диаграмма D^τ (2) при θ = 1. k нейронов соответственно с n₁... ..., nk входами, расположенными в одном ранге, образуют одноранговую сеть с k выходами. Порог θⁱ каждого нейрона изменяется независим от порогов остальных нейронов, i = 1,..., k. Квазирезультирующие диаграммы нейронов при фиксированном значении их порогов строятся отдельно для каждого нейрона. Они представляют второй ранг двухранговой сети диаграмм Венна с k выходами.

Первый ранг этой сети образуют n диаграмм Венна n переменных, где n - число различных входов исходной сети формальных нейронов. При этом входы а₁,....,а_n воспринимаются как переменные, а диаграммы (n) находятся аналогично § 1.3 (см. построение диаграмм по данным формулам), т. е. D^τ_1,i (n) ↔ D^τ [a_i], i = 1,... ..., n. От диаграммы D^τ_1,i (n) к диаграмме D^τ_2,j проводится кривая с номером / тогда и только тогда, когда a_i является l-тый входом j-того нейрона, квазирезультирующей диаграммой которого является D^τ_2,j.

Результирующие диаграммы полученной двухранговой сети будем называть результирующими диаграммами исходной сети нейронов при данных значениях их порогов.

При изменении значений порогов нейронов операторы второго, ранга сети диаграмм Венна могут изменяться.

Легко убедиться, что при k = 1 получим двухранговую сеть диаграмм Венна, эквивалентную одноранговой сети, соответствующей этому нейрону, как сети с одним выходом при этом же значении порога θ.

Пример 2.1 (продолжение). Рассматривая нейрон на рис. 2.1 как сеть из k элементов, k = 1, получим при θ = 1 двухранговую сеть (рис. 2.2), эквивалентную одноранговой сети, расположенной справа от нейрона на рис. 2.1.

Пример 2.3 На рис. 2.3 дана одноранговая сеть с четырьмя входами и двумя выходами, n₁ = 2, n₂ = 3. При θ¹ = 2, θ² = 1 квазирезультирующие диаграммы совпадают с операторами сети примера 1.9.

Соответствующая двухрангорая сеть построена на рис. 2.4.

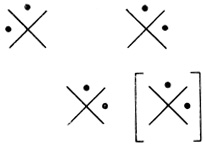
Рис. 2.2

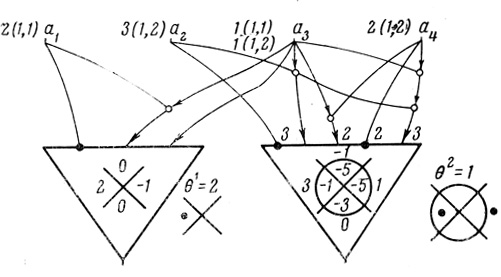
Рис. 2.3

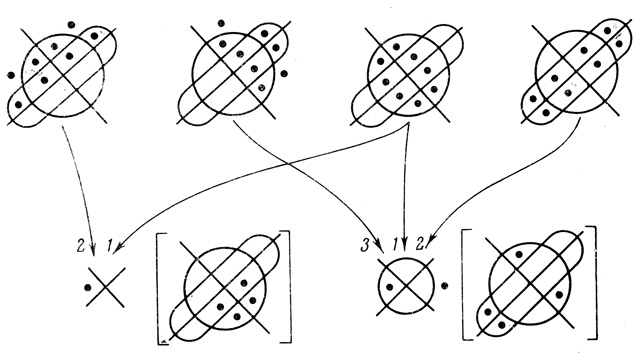
Рис. 2.4

Многоранговые сети формальных нейронов. Сети формальных нейронов, имеющие несколько рангов, называются многоранговыми.

В первом ранге многоранговых сетей находится kx формальных нейронов соответственно с n₁,...,n_k1 входами; все входы первого ранга независимы. В r-том ранге - k_r нейронов соответственно с n_{k1+...+kr-1+1},.......,n_k1+....+kr входами, 1 < r ≤g, g - число рангов в сети; входами каждого нейрона в r-том ранге могут быть только входы сети (входы сети есть все различные входы нейронов первого ранга) или выходы нейронов, расположенных в первом, во втором,... в (r - 1)-м рангах.

Порог θ^r,i каждого нейрона (r - номер ранга, i - номер нейрона в ранге, r = 1,..., g, i = 1,...., k_r) изменяется независимо от порогов остальных нейронов сети.

Квазирезультирующие диаграммы нейронов при фиксированном значении их порогов строятся отдельно для каждого нейрона сети. Число переменных каждой квазирезультирующей диаграммы равно числу входов соответствующего нейрона.

Квазирезультирующие диаграммы всех нейронов r-того ранга, r = 1,..., g, образуют (r + 1)-й ранг сети G диаграмм Венна, состоящей из (g + 1)-го ранга. Количество выходов сети G совпадает с количеством выходов исходной сети формальных нейронов.

В первом ранге сети G расположено n диаграмм Венна D^τ_1,1 ... ...,D^τ_1,n, каждая n переменных, где n-число различных входов а₁,...,а_n данной сети формальных нейронов. Диаграммы i = 1,..., n, строятся аналогично диаграммам Венна первого ранга двухранговой сети, которая соответствует одноранговой сети формальных нейронов с несколькими выходами.

От диаграммы D^τ_s,i к диаграмме сети G (s = 1,..., r = 1; i = 1,..., k_s; r = 2,..., g + 1; j = 1,..., k_r) проводится кривая с номером I тогда и только тогда, когда ш является /-тым входом j-того нейрона A_r,j (в r-том ранге) для случая s = 1 или D^τ_s,i - квазирезультирующей диаграммой нейрона A_s,i, выход которого есть j-тый вход нейрона A_r,j для случая s > 1.

Результирующие диаграммы сети G воспринимаем как результирующие диаграммы исходной сети формальных нейронов при фиксированных значениях порогов всех нейронов сети.

При изменении значений порогов нейронов сети соответствующие операторы r-того ранга (r > 1) сети G могут изменяться.

Пример 2.4. На рис. 2.5 дана двухранговая сеть формальных нейронов с тремя входами и одним выходом, n₁ = 3, n₂ = 3, n₃ = 2, n₄ = 4. При θ^1,1 = 1, θ^1,2 = 2, θ_1,3 = 1, θ^2,1 = 1 получаем трехранговую сеть, показанную на рис. 2.6.

Регулярные сети формальных нейронов. Сеть формальных нейронов называем регулярной, если она построена следующим образом.

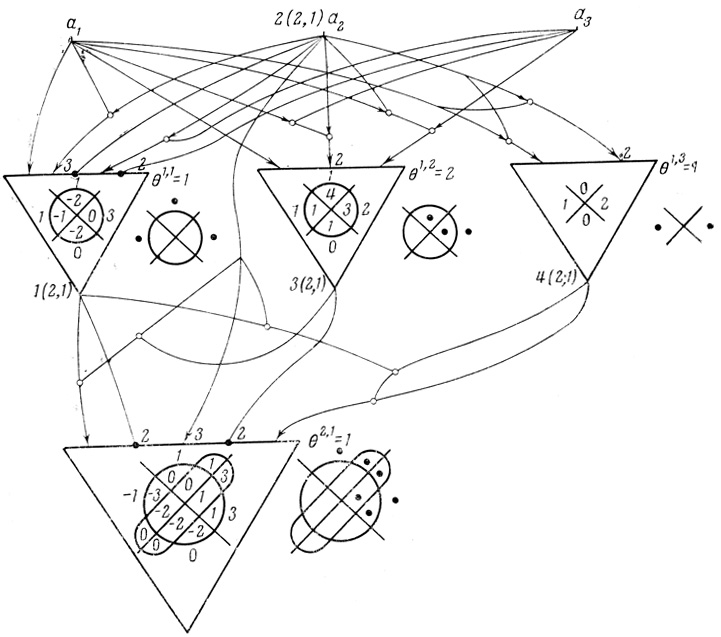
Рис. 2.5

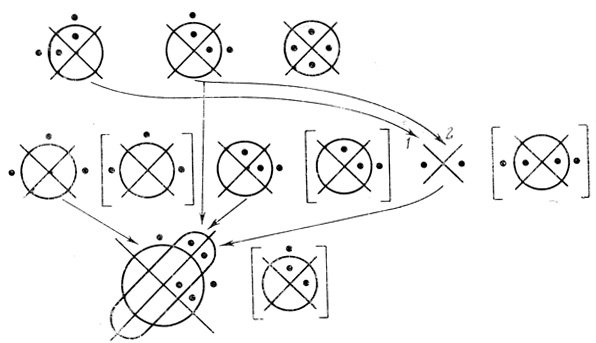
Рис. 2.6

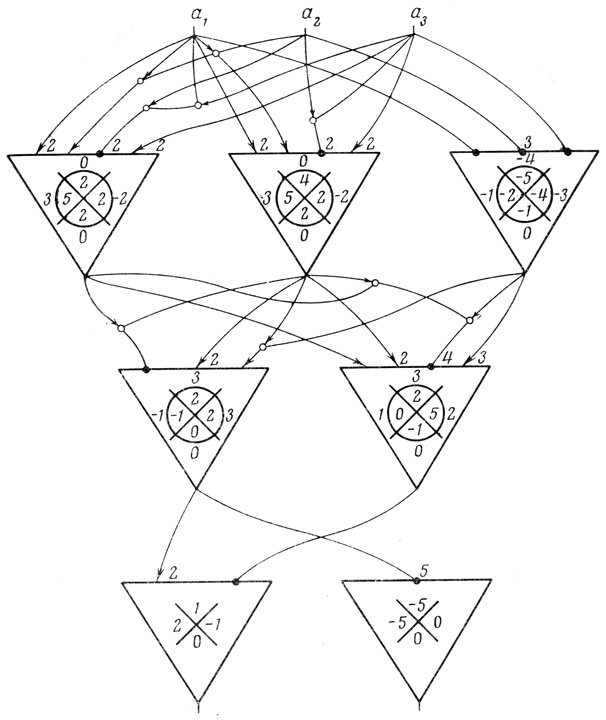
Рис. 2.7

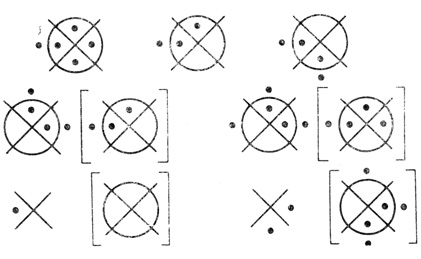
Рис. 2.8

Сеть имеет n входов которые являются различными входами n_r нейронов первого ранга. Входами n_r нейронов r-того ранга (r > 1) могут быть только выходы нейронов (r - 1)-го ранга. При этом предполагается, что все выходы нейронов (r - 1)-го ранга, r > 1 (при r = 1 говорится о входах сети), являются входами нейронов r-того ранга, которые нумеруются слева направо (в этом случае номера входов можно не писать).

Из построения следует, что в сети диаграмм Венна, соответствующей регулярной сети формальных нейронов при фиксированных значениях порогов всех нейронов, результирующие диаграммы первого ранга совпадают с операторами первого ранга (в предположении, что число переменных на-результирующей диаграмме равно числу переменных на соответствующем операторе). Поэтому в сетях диаграмм Венна, соответствующих регулярным сетям формальных нейронов, первый ранг можно не строить. При этом будут получаться g-ранговые регулярные сети диаграмм Венна, где g - число рангов в исходной сети формальных нейронов.

Регулярную сеть формальных нейронов будем называть просто регулярной, если число входов и число нейронов во всех рангах, кроме последнего, одинаково, а в последнем ранге - один нейрон. Такие сети рассматриваются, например, в работах [13, 16].

Пример 2.5. На рис. 2.7 дана трехранговая регулярная сеть с тремя входами и двумя выходами, n = 3, n₁ = 3, n₂ = 2, n₃ = 2. На рис. 2.8 - соответствующая трехранговая регулярная сеть диаграмм Венна при θ^1,1 = 2, θ^1,2 = 3, θ^1,3 = - 2, θ^2,1 = 2, θ^2,2 = 1, θ^3,1 = 2, θ^3,2 = 0.