§ 2.2. Обобщение понятия формального нейрона

В § 0.3 дано определение формального нейрона в смысле Мак-Каллока. При этом подчеркивается, что, кроме запрещающих волокон, оканчивающихся на волокнах, направленных на тело нейрона (см. [13, 16,26]), можно рассматривать запрещающие волокна, оканчивающееся на других запрещающих волокнах,- так называемые волокна типа "Запрет запрета". Введение этого типа волокон, как показано в следующей главе, может' привести к уменьшению общего числа необходимых волокон нейрона.

В настоящем параграфе приводится обобщение понятия формального нейрона. В частности, предполагается, что волокна нейронов могут не только ветвиться, но и объединяться. Получающиеся при этом вершины (точки объединения) играют роль задержек сигналов на единицу времени.

Ясно, что при большом числе волокон наглядность геометрического изображения нейрона уменьшается. Поэтому, а также в целях- уточнения понятия, установим соответствие между некоторыми так называемыми нейронными словами в алфавите и формальными нейронами (об алфавитах и словах в алфавитах см. [27]).

Для описания функционирования формальных нейронов с n выходами вводятся Т-диаграммы n переменных. Т-диаграммы позволяют в каждый данный момент времени определить слово (называемое входным), соответствующее возбужденным (активированным) волокнам, направленным на тело нейрона.

Как и в § 0.3, нейрон имеет тело, порог, конечное число входов a₁,....,а_n и один выход. Тело нейрона на рисунках изображается треугольником. Входы нейрона не находятся на теле и не касаются его. Выход расположен на теле нейрона. Входы и выход могут находиться только в одном из двух состояний - возбужденном или невозбужденном. Порог 0 нейрона выражается числом, он может изменяться в некоторых пределах {θ₁,..., θ_r}, где θ₁,..., θ_r - различные целые числа, расположенные в порядке убывания. Сигналы (возбуждения) могут проходить только в одном направлении - от входов к выходу.

Нейрон может иметь волокна. Типы волокон такие же, как и описанные в § 0.3: возбуждающие, тормозящие и запрещающие, но каждое волокно может иметь более сложную структуру.

Строение волокна α. Первый ярус. Все входы нейрона a₁,..., а_n и только они являются входами первого яруса.

Некоторую точку b_j, отличную от входов первого яруса, будем называть вершиной первого яруса, если существуют входы первого яруса a_i1,..., a_ik, 0 < k ≤ n, которые соединяются одной или несколькими незамкнутыми кривыми Жордана с точкой b_j, т. е. от каждого из входов a_i1,..., a_ik до точки b_j проводится одна или не сколько линий. Эти линии будем называть ребрами первого яруса. Началом каждого ребра является вход первого яруса, концом - вершина b_j. Будем предполагать, что никакие два различных ребра не могут объединяться и не могут иметь общих кусков.

Каждое ребро может осуществлять передачу сигналов от входов, первого яруса к вершине b_j. О вершине b_j будем говорить в этом случае, что она связана о. входами a_i1,..., a_ik. В примерах вершина b_j обозначается жирной точкой и располагается ниже входов нейрона. Вершины первого яруса между собой не соединяются. От каждой вершины первого яруса проведено по крайней мере одно ребро к вершинам следующих ярусов.

Второй ярус. Пусть b₁,...,b_m - все различные вершины первого яруса.

Входы и вершины первого яруса являются входами второго яруса.

Вершины и ребра второго яруса определяются аналогично соответствующим понятиям первого яруса. При этом от вершин первого яруса к данной вершине второго яруса может проводиться только одно ребро.

Если вершина с второго яруса связана с вершиной b первого яруса, а вершина b связана с входами нейрона a_i1,....,a_is, то будем говорить, что вершина с связана с входами a_i1,.....,a_is, итак далее.

Последний (q-тый) ярус волокна а имеет только одну вершину.

От вершины последнего яруса (при q = 0 от некоторого входа нейрона) проведем ребро, оканчивающееся стрелкой (если α - возбуждающее волокно), точкой (если а- тормозящее волокно), петлей (если α - запрещающее волокно).

Запрещающее волокно оканчивается на некотором ребре другого волокна, которое при этом называется запрещаемым ребром. Запрещающие волокна проводятся так, что в каждый данный момент ясно, какое ребро какими волокнами запрещается.

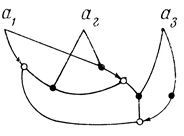
Рис. 2,9

Определение. Будем говорить, что запрещающие волокна ξ₁,......,ξ_l, l > 1 образуют замкнутую цепь, если волокно ξ_j- оканчивается на некотором ребре волокна ξ_j+1, j = 1,..., l - 1, а волокно ξ_l - на некотором ребре волокна ξ₁.

Примеры замкнутых цепей запрещающих волокон приведены на рис. 0.3 и 2.9.

Будем предполагать, что запрещающие волокна нейрона замкнутых цепей не образуют.

Возбуждающие и тормозящие волокна оканчиваются на теле нейрона.

Пример возбуждающего волокна приведен на рис. 2.10, где а₁, а₂, а₃, а₄ - входы нейрона; q = 3.

Ребра волокон нейрона могут находиться только в одном из двух состояний: возбужденном или невозбужденном.

Ребро у первого яруса, началом которого является вход a_i первого яруса, может быть возбуждено только тогда, когда возбужден вход а,. В случае возбуждения ребра у возбужден и его конец - вершина первого яруса, являющаяся входом во второй ярус.

Аналогично будем говорить о возбуждении ребер и вершин t-того яруса, 1 < i ≤ q.

Ребро, проведенное из вершины последнего (g-того) яруса, может быть возбуждено только тогда, когда возбуждена вершина последнего (q-того) яруса.

Волокно нейрона считается возбужденным только тогда, когда возбуждено ребро, проведенное от вершины последнего яруса.

Возбуждение запрещающего волокна означает, что запрещаемое им ребро не возбуждается (даже в том случае, когда это же ребро, но без запрещающего волокна, было бы возбуждено).

Вопрос об условиях возбуждения нейрона будет разбираться несколько ниже.

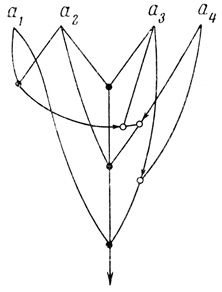
Рис. 2.10

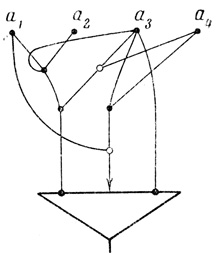
Рис. 2.11

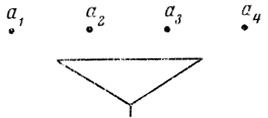
Рис. 2.12

Примеры формальных нейронов. На рис. 0.1 - нейрон в смысле Мак-Каллока. На рис. 2.11 - обобщенный нейрон с четырьмя входами: а₁, а₂, а₃, а₄. На теле нейрона оканчиваются три волокна. Первое (слева направо) волокно тормозящее, оно имеет два яруса (q = 2); в первом ярусе находится одна вершина, соединенная ребрами с входами а₃, a₁, а₂, во втором ярусе - также одна вершина, соединенная ребрами с вершиной первого яруса и с входом а₃; на ребре, соединяющем вершину второго яруса с входом а₃, оканчивается запрещающее волокно от входа а₄. Второе волокно возбуждающее, q = 1, вершина соединена с входами а₃ и а₄ на ребре, направленном на тело нейрона, оканчивается запрещающее волокно от входа a₁. Третье волокно тормозящее, q = 0, началом волокна является вход а₃.

На рис. 2.12 показан нейрон с четырьмя входами без волокон.

Нейронные слова. Пусть Б - алфавит, Б̃ - алфавит двойников алфавита Б, Б a₁...а_n, Б̃ а̃₁... а̃_n, где a_i - буква алфавита Б, ã_i - двойник буквы a_i, i = 1,..., n (об алфавитах, буквах, их двойниках см. [27]). Пусть скобки (, ), [,], <,> не принадлежат алфавиту ББ.

Нейронные слова (для краткости TV-слова) в алфавите В, В ↔ ББ̃ ( ) [ ] < >, определяем индуктивно:

1) если а - буква алфавита ББ̃, то а - N-слово;

2) пустое слово есть N-слово;

3) если β - N-слово в алфавите Д,Д, ↔ Б ( ) [ ], β≠Λ, то [β] - слово вида N₁, <β> - слово вида N̄₁;

4) если β - буква алфавита ББ̃ или β - слово вида N₁ или N̄₁ γ -не пустое N-слово в алфавите Д, то β (γ)-слово вида N₂;

5) если β - слово вида N₂, γ - N-слово в алфавите Д, γ≠Λ, то β(γ) - слово вида N₂;

6) если β - слово вида N₁, или N̄₁ или N₂, то β - N - слово;

7) Если β - непустое N-слово, γ - буква алфавита ББ̃ или Y - слово вида N₁ или N₁ или N₂, то βγ - N-слово.

Слова, определяемые в пунктах 1, 3, 4, 5, будем называть элементарными.

Всякому N-слову можно поставить в соответствие дерево его построения, каждому узлу которого соответствует один (и только один) из шагов построения 1-5,7. Так, N-слову а₁ < а₂а₃ [а₁а₂]} а̃₃ (а₂) соответствует его дерево построения по шагам (рис. 2.13). Номер шага есть его имя, слева от N-слов - номера правил построения.

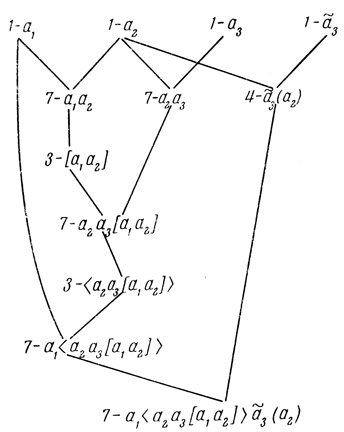
Рис. 2.13

Нетрудно показать, что дерево построения N-слова определяется им (N-словом) однозначно, т. е. что при чтении N-слов не может возникнуть омонимия. Доказательство этого нетрудно провести аналогично тому, как доказываются обычные теоремы о скобках (см., например, [28]).

Соответствие между N-словами и формальными нейронами

1. Пусть β - N-слово. Построим формальный нейрон, соответствующий слову β.

Пусть а₁,...а_n - все различные буквы алфавита Б. Поставим им в соответствие входы нейрона, которые будем обозначать этими же буквами а₁,..., а_n.

Если в слове β нет вхождений буквы a_i то будем говорить, что у соответствующего нейрона вход a_i является фиктивным.

Построение волокон нейрона будем вести индукцией по построению слова Р (пункт 6 определения N-слова в построении не участвует) .

Пусть βa_i, a_i ∈ Б (пункт 1 определения N-слова).

От входа a_i на тело нейрона проведем возбуждающее волокно. Получим нейрон, соответствующий N-слову β.

Пусть βã_i, ã_i ∈ Б (пункт 1).

От входа a_i на тело нейрона проведем тормозящее волокно. Получим нейрон, соответствующий N-слову β.

Пусть βΛ (пункт 2).

Тогда все входы нейрона фиктивны. Будем считать, что это соответствует случаю, когда нейрон не имеет волокон.

Пусть β - слово вида N₁, β[β₁], где β₁ - непустое N-слово в алфавите Д (пункт 3). Предположим, что волокна, соответствующие N-слову β₁, проведены.

Волокна, соответствующие N-слову β₁ и направленные на тело нейрона, соединим между собой, уничтожив на них стрелки (так, как это показано ниже в примере 2.6). От точки соединения на тело нейрона проведем ребро, оканчивающееся стрелкой. Получим нейрон, соответствующий N-слову β.

Пусть β - слово вида N̄₁, ββ₁> где β₁ - не пустое N-слово в алфавите Д (пункт 3). Предположим, что волокна, соответствующие N-слову β₁, проведены.

Волокна, соответствующие N-слову β₁ и направленные на тело нейрона, соединим между собой, уничтожив на них стрелки (так, как это показано ниже в примере 2.7). От точки соединения на тело нейрона проведем ребро, оканчивающееся жирной точкой. Получим нейрон, соответствующий N-слову β.

Пусть β - слово вида N₂, ββ₁(β₂) где β_i, i = 1,2 - непустые N-слова; β_2ΩД (знак Ω - сокращение записи "слово в алфавите"); β₁ - буква алфавита ББ̃, или - слово вида Nl₁ или N̄₁ или N₂ (пункты 4 и 5). Предположим, что волокна, соответствующие N-словам β₁ и β₂, проведены.

Волокна, соответствующие N-слову β₂ и направленные на тело нейрона, соединим между собой. От точки соединения проведем ребро, оканчивающееся петлей на ребре волокна, соответствующего N-слову β₁, направленному на тело нейрона. Получим нейрон, соответствующий N-слову β (см. ниже пример 2.8).

Пусть ββ₁β₂, где β₁ - непустое N-слово; β₂ - элементарное слово (пункт 7). Предположим, что волокна, соответствующие N-слову β₁, проведены.

После всех волокон, соответствующих N-слову β₁, проведем волокно, соответствующее N-слову β₂. Получим нейрон, соответствующий N-слову β.

2. Пусть, наоборот, нам дано не N-слово, а нейрон А с входами а₁,..., а_n, по которому нужно построить соответствующее ему N-слово β. Опишем процесс построения такого слова.

Если нейрон А не имеет волокон, то βΛ.

Если b_i есть i-тое волокно нейрона, оканчивающееся на теле нейрона, то просматриваем его (i-тое волокно), начиная с корня (корень волокна - стрелка или жирная точка на теле нейрона). Если волокно имеет несколько ребер, то просматриваем их последовательно слева направо. Запрещающие волокна просматриваем во вторую очередь.

Будем говорить, что запрещающие волокна, петельки которых находятся на ребрах рассматриваемого волокна b_i, также образуют ребра волокна b_i, петельки являются вершинами, а сами волокна b_i, оканчивающиеся на теле нейрона, в этом случае будем называть нейронными деревьями (для краткости, N-деревьями).

Таким образом, получаются N-слова β₁,..., β_k, где k - число волокон нейрона, оканчивающихся на теле нейрона (т. е. k - число N-деревьев нейрона). N-слово ββ₁,..., β_k будем считать словом, соответствующим данному нейрону А.

2.1. Если корень N-дерева b_i есть стрелка, то β_i - буква алфавита Б, или β_i - слово вида N₁ или β_i - слово вида N₂.

2.1.1. β_i-буква алфавита Б, если N-дерево b_i имеет только одно ребро без петель - от стрелки до входа a_j⋅β_ia_j.

2.1.2. β_i - слово вида N₁, если, поднимаясь от корня, первой встретим вершину, β_i[D_1,i, ..., D_r,i], где D_r,i - N-слова, соответствующие ребрам последнего яруса, оканчивающимся в этой вершине.

2.1.3. β_i- - слово вида N₂, если, поднимаясь от корня, первой встретим петельку, запрещающую возбуждение рассматриваемого волокна (в случае возбуждения запрещающего волокна). β_iD_i(E_i), где E_i - N-слово, соответствующее запрещающему волокну; D_i - N-слово, соответствующее запрещаемому волокну; D_iΩД; началом слова Di является или буква алфавита Б̃, или [.

2.2. Если корен дерева b_i есть точка, то β_i - буква алфавита Б̃, или β_i - слово вида N₁, или β_i - слово вида N₁.

2.2.1. β_i - буква алфавита Б̃, если дерево имеет только одно ребро без петель - от точки до входа а_j ⋅ β_ja_j.

2.2.2. β_i - слово вида N̄₁ если, поднимаясь от корня, первой встретим вершину. β_i<D_1,i,.....,D_r,i> где D_1,i,......,D_r,i слова, соответствующие ребрам последнего яруса, оканчивающимся в этой вершине.

2.2.3. β_i - слово вида N₂, если, поднимаясь от корня, первой встретим петельку, запрещающую возбуждение рассматриваемого волокна (в случае возбуждения запрещающего волокна). β_iD_i(E_i), где E_i - N-слово, соответствующее запрещающему волокну; E_i - N-слово, соответствующее запрещаемому волокну; E_i Ω Д; началом слова D_i является или буква алфавита Б̃, или <.

Из однозначности чтения N-слов и установленного соответствия между N-словами и нейронами следует, что если β - N-слово, А - нейрон, построенный по слову β, β₁ - N-слово, построенное по нейрону A, то β_iβ.

Примеры:

2.6. Пусть β [а₁ [а₁ а₂]] и алфавит Б есть a₁a₂a₃. Построим нейрон, соответствующий N-слову β:

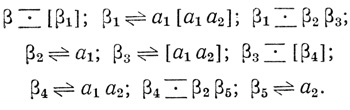
а) Построим нейрон, соответствующий N-слову β₂ (рис. 2.14).

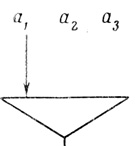
Рис. 2.14

б) Построим нейрон, соответствующий N-слову β₃ (рис. 2.15).

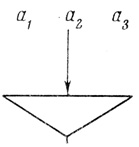
Рис. 2.15

в) Построим нейрон, соответствующий N-слову β₄ (рис. 2.16).

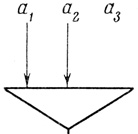
Рис. 2.16

г) Построим нейрон, соответствующий N-слову β₃ (рис. 2.17).

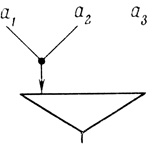
Рис. 2.17

д) Построим нейрон, соответствующий N-слову β₁ (рис. 2.18),

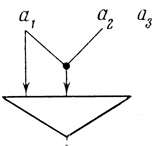
Рис. 2.18

е) Построим нейрон, соответствующий N-слову β (рис. 2.19).

У построенного нейрона вход а₃ является фиктивным.

2.7. Пусть β < [а₁а₂]>, Б а₁а₂а₃. Построим нейрон, соответствующий N-слову р.

Построение ведется аналогично примеру 2.6, п. "а" - "д":

β<β₁>

е) Построим нейрон, соответствующий N-слову β (рис. 2.20).

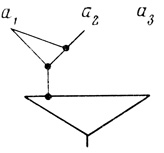
Рис. 2.20

2.8. Пусть β<a₁[a₁a₂]>(a₃)Б а₁а₂а₃. Построим нейрон, соответствующий N-слову β:

ββ₁(β₂); β₁↔<a₁[a₁a₂]>; β₂↔a₃

О построении нейрона, соответствующего слову β₁, см. пример 2.7.

Нейрон, соответствующий N-слову β₂, приведен на рис. 2.21.

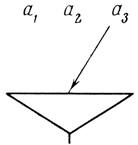
Рис. 2.21

Следовательно, нейрон, соответствующий N-слову β, имеет вид, приведенный на рис. 2.22.

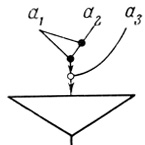
Рис. 2.22

Операция N-вычеркивания. Пусть β - непустое N-слово. Пусть в β выделено (подчеркнуто) конкретное вхождение непустого N-слова β₁, основу этого вхождения обозначим β₁*.

В слове β вычеркнем β₁* вместе со всеми следующими за ним вполне круглыми словами.

Понятие "вполне круглое слово" для N-слов определяется следующим образом.

Если β - N-слово, то (β) является вполне круглым словом с основой β.

Аналогично определяются вполне квадратные и вполне уголковые слова.

В получившемся из слова β слове вычеркиваем все слова ( ), [ ], < > (т. е. вполне круглые, вполне квадратные, вполне уголковые слова с пустой основой) до тех пор, пока не получим некоторое слово D, в которое не входят эти слова ( ), [ ], < >.

Полученное слово D называем результатом операции N-вычеркивания. Нетрудно убедиться, что D является N-словом.

Примеры:

2.9. β↔a₁ (a̱₂ (a₃ [a₁])). Тогда Da₁.

2.10. β↔a̱₁(a₂(a₃ [a₁])). Тогда DΛ.

2.11. β↔a₁(a̱₂ (a₃[a₁])]). Тогда Da₁.

Входные слова формального нейрона. Пусть А - нейрон с входами а₁,..., а_n, В каждый данный момент времени входы и выход нейрона могут находиться только в одном из двух состояний - возбужденном или невозбужденном. Поэтому в каждый данный момент времени входы нейрона образуют только одну элементарную последовательность из n нулей и единиц (единица, стоящая на i-том месте, соответствует возбужденности входа нуль, стоящий на j-том месте, соответствует не возбужденности входа а_j).

Всех возможных элементарных последовательностей n переменных - 2ⁿ.

Каждой элементарной последовательности а переменных a₁,..., а_n поставим в соответствие N-слово.

Пусть для определенности не возбуждены только входы а_i1,..., a_ik, 0 ≤ k ≤ >n (k = 0 означает, что все входы нейрона возбуждены).

Пусть β - N-слово, соответствующее нейрону А.

Выполним последовательно следующие операции над словом β:

1) N-вычеркнем из β все буквы а_ij, ã_ij, j = 1,..., k.

Получим N-слово β₁;

2) N-вычеркнем из N-слова β₁ последовательно все подслова вида N₂, в которые не входят никакие подслова вида N₂. Получим N-слово β₂.

К слову β₂ применим операцию 2 и так далее, пока не получим N-слово, не содержащее подслов вида N₂.

Полученное слово будем обозначать β_α и называть входным словом, соответствующим элементарной последовательности α.

Примеры (в примерах 2.12, 2.13 три входа; а₁, а₂, а₃).

2.12. β↔a₁(a₂(a₃(a₁))); α↔110;

Тогда β₁a₁(a₂); β₂Λ; β_αΛ

2.13. β↔a₁(a₂(a₃(a₁))); α↔111;

Тогда β₁β; β₂a₁(a₂); β₃Λ; β_αΛ.

Если все входы нейрона не возбуждены, то β_αΛ.

Таким образом, в каждый данный момент времени вычисляется определенное входное слово, которое соответствует возбужденным волокнам, направленным на тело нейрона. При этом запрещаемые ребра вместе с запрещающими волокнами не учитываются. Слова вида N₂ соответствуют волокнам с запретами, а возбуждение запрещающего волокна означает, как принято в настоящей работе, что запрещаемая им ветвь N-дерева волокна не возбуждена.

Всего входных слов нейрона, соответствующих различным элементарным последовательностям, 2ⁿ среди них есть по крайней мере одно пустое слово. Будем говорить, что все 2ⁿ входные слова нейрона образуют Т-диаграмму нейрона. Для представления Т- диаграммы можно использовать символ Венна n переменных.

Пример 2.14. W-слово, соответствующее нейрону рис. 0.1, имеет вид a₁ã³₁ (a₃) (ã₂) ã₂a²₂ (a₃)ã₃ где а̃₁³(а₃) (a₂) - сокращение записи ã₁(a₃)(a₂)ã₁(a₃)(a₂)ã₁(a₃)(a₂) -сокращение а²₂(а₃)а₂ (а₃).

Выпишем все входные слова.

Аналогично см. Т-диаграмму на рис. 2.23, где возбужденность входа a_i обозначается a_i, а не возбужденность - ā_i.

Если предположить, что вершины волокон нейрона играют роль задержек сигналов на единицу времени, то Г-диаграммы нейрона будут зависеть от момента времени, в который рассматривается нейрон. В каждый данный момент времени нейрон будет иметь соответствующую Т-диаграмму. На рисунках слева от вершины указываем время их возбуждения, предполагая, что t - момент времени, в который входы нейрона образуют определенную элементарную последовательность, при этом корень волокна рассматривается как вершина.

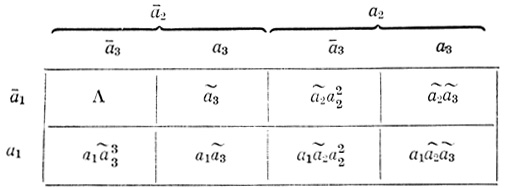
Рис. 2.23

В N-слове, построенном по нейрону, вершинам, отличным от корней, соответствуют скобки. Каждой вершине волокна соответствует одна собственно спаренная пара скобок^*. Если волокно возбуждающее, то его вершинам соответствуют квадратные скобки. Если волокно тормозящее и если оно имеет вершины, кроме вершин запрещающих волокон, оканчивающихся на его ребрах, то первой вершине от корня соответствуют угловые скобки, а остальным квадратные.

^* (Допустим, что у нас имеется 2ⁿ скобок (например, квадратных), из них n левых и n правых, и что они расположены в линейном порядке слева направо (между ними могут находиться другие символы).

Легко видеть, что все скобки в любом N-слове собственно спарены.)

В каждый данный момент времени t + i, i ≥ 1, вместо N-слова β, соответствующего нейрону, рассматриваем N-слово β₁, которое строится только по тем ребрам волокон нейрона, по которым сигнал (возбуждение) может прийти на тело в t + i момент времени. Используя операцию N-вычеркивания, можно сказать, что N-слово β_i получается из β N-вычеркиванием:

а) всех тех элементарных слов, которые соответствуют волокнам, оканчивающимся на теле нейрона, и у корня которых слева не стоит t + i;

б) всех тех элементарных слов, которые соответствуют ветвям, рассматриваемым в один из предшествующих моментов времени t + u, u < i.

в) всех элементарных слов, соответствующих ветвям, начинающимся в вершинах (q - j + 1)-го яруса, около которых слева не находятся t + i - j(j = 1,..., i), q - число ярусов волокна; считаем, что N-слово, соответствующее запрещающему волокну с петелькой на ребре, оканчивающемся в (q - j + 1)-м ярусе, сохраняется только тогда, когда это ребро не уничтожается и когда около петельки слева есть t + i - j.

Само собой разумеется, что правила преобразования N-слова β в N-слово β_i можно сформулировать независимо от геометрического представления нейрона, обращая внимание, например, на число пар квадратных и уголковых скобок в элементарных словах.

Из построения N-слов β, вытекает, что, если i > δ + 1, где δ = max {δ₁,..., δ_l} (δ_k - число вершин k-того волокна, оканчивающегося на теле нейрона, не включая корень волокна и вершины запрещающих волокон, петельки которых находятся на его ребрах, k = 1,..., l, l - число волокон с весом, оканчивающихся на теле нейрона), то β_iΛ Т-диаграммы N-слов β_i, соответствующих различным моментам времени t + i, будем называть T_i-диаграммами.

Пример 2.15. Нейрону на рис. 2.24. соответствует N-слово

βa²₂[[[[a₁]]]]⁴ [[[[a₁а₂] а₃] ([а₂а₄])] а₂а₃а₄]³а̃₃<[а₄]>⁵,

В момент времени t + 1 около 2, 3 и 5-го волокон (считая корни волокон на теле нейрона слева направо) слева нет t + 1, поэтому β₁a²₂ã₃.

В момент времени t + 2 около 1, 2, 4 и 5-го волокон слева не стоит t + 2, около вершины третьего яруса 3-го волокна нет t (около вершин третьего яруса t находиться не может в силу принятых выше условий прохождения сигналов), поэтому β₂[a₂a₃a₄]³.

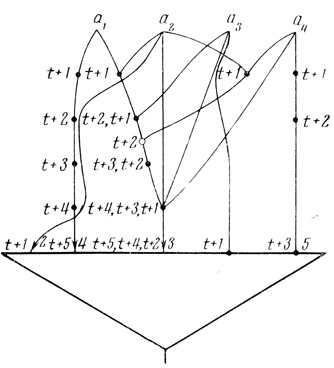
Рис. 2.24

В момент времени t + 3 около 1-4-го волокон нет t + 3, поэтому β₃ <[a₄]>⁵

В момент времени t + 4 около 1, 2, 4 и 5-го волокон не стоит t + 4, около вершины первого яруса 3-го волокна нет t, а ребра, соединяющие входы а₂, а₃ и а₄ с вершиной четвертого яруса 3-го волокна, рассматривались в момент t + 2, поэтому β₄[[[a₃]([a₂ã₄])]]³.

В момент времени t + 5 около 1, 4 и 5-го волокон слева нет t + 5, около петельки запрещающего волокна на 3-м волокне нет t + 3, а ребра, соединяющие вход а₃ с вершиной второго яруса и входы а₂, а₃ и а₄ с вершиной четвертого яруса, рассматривались соответственно в моменты времени t + 4 и t + 2, поэтому β₅[[[a₁]]]]⁴[[[[a₁a₂]]]]³.

В моменты времени t + i, i > 5, β_iΛ.

Т-диаграмма и T_i-диаграммы соответственно N-слов β и β_i, i ≥ 1 построены на рис. 2.25.

Для формальных нейронов в смысле Мак-Каллока β_iΛ, если i > 1, ββ₁ и следовательно, T₁-диаграмма графически равна Т-диаграмме.

Т-диаграммы n переменных. Входное слово - это такое N-слово, в которое не входят слова вида N₂. Поэтому входные слова можно рассматривать независимо от формальных нейронов, как те N-слова, в построении которых не применяются пункты 4 и 5 определения N-слова.

Т-диаграммой n переменных будем называть 2ⁿ произвольных входных слов, среди которых есть по крайней мере одно пустое слово и которые поставлены в соответствие всем 2ⁿ различным элементарным последовательностям n переменных, при этом последовательности 0...0 (n нулей) соответствует пустое слово. Т-диаграммы n переменных удобно представлять с помощью символа Венна n переменных.

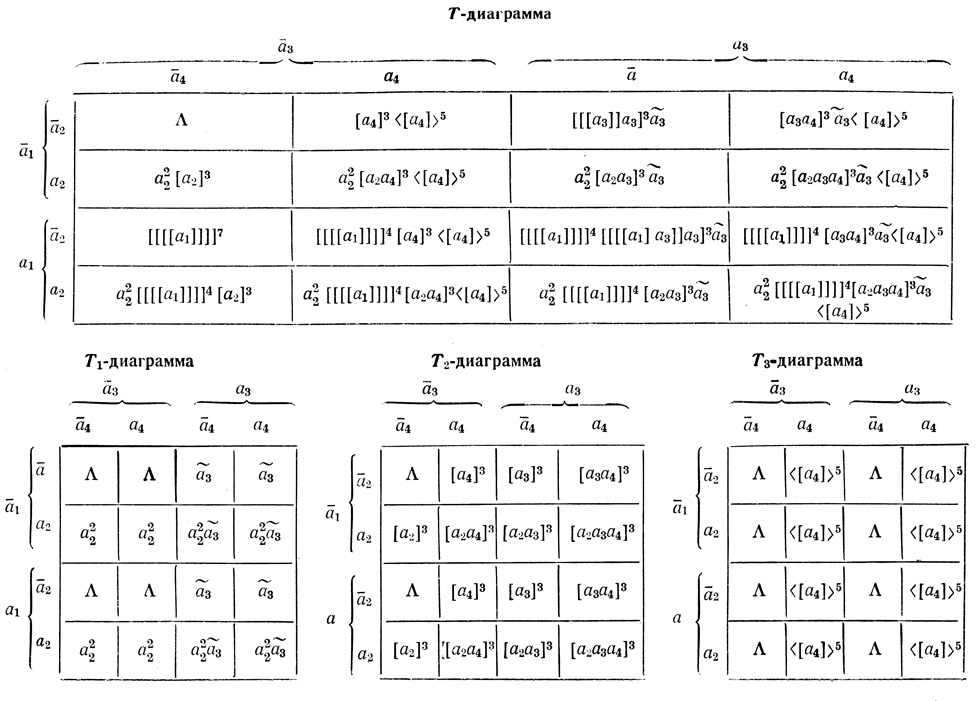
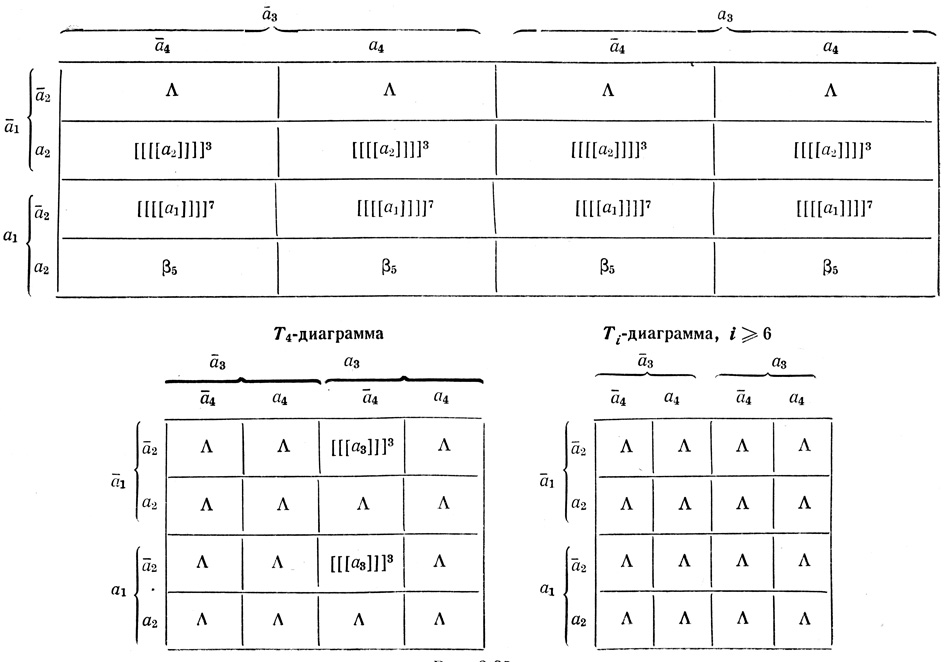
Рис. 2.25

Т-диаграмму n переменных будем обозначать D^T, иногда указывая справа в круглых скобках число переменных или сами переменные.

Например, на рис. 2.25 приведено семь Т-диаграмм четырех переменных, для представления которых используются таблицы Венна четырех переменных.

Выше показано, как для любого нейрона с n входами построить а) Т-диаграмму n переменных, описывающую возбужденные волокна данного нейрона в зависимости от элементарных последовательностей, которые образуют его входы; б) Т_i-диаграммы n переменных, описывающие возбужденные волокна нейрона в различные моменты времени в зависимости от элементарных последовательностей, которые образуют его входы.

Возникают обратные задачи: а) по данной Т-диаграмме D^T (n) построить нейрон, возбуждение волокон которого описывается диаграммой D^T (n); б) по данным 6 различным Т_i-Диаграммам n переменных i = 1,..., 6, построить нейрон, Т_i-диаграммы которого совпадают с данными.

К этим задачам вернемся в следующей главе, а сейчас перейдем к условиям возбуждения формальных нейронов.

По данному входному слову β определим индукцией по его построению целое число, которое будем называть весом слова β и обозначать :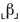

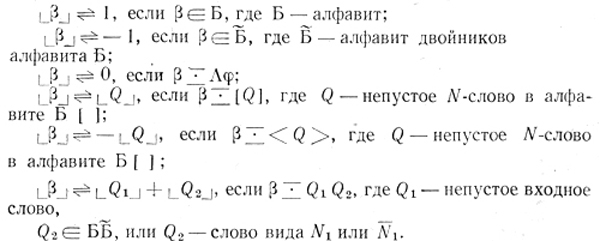
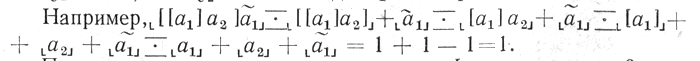
Понятно, что по данному целому числу L входное слово β, для которого 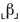= L, строится неоднозначно.

Два N-слова Q₁ и Q₂ будем называть N-равными, если для любой элементарной последовательности переменных а₁,..., а_n имеет место равенство

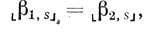
где а₁,..., а_n - графически различные буквы, из которых составлены Q₁, Q₂ (предполагается, как и всюду в дальнейшем, если не оговорено противное, что буква отлична от любой скобки), β_i,s - входное слово в s-той ячейке на Т-диаграмме N-слова Q_i (Т-диаграммой N-слова Q называем Т-диаграмму нейрона, соответствующего слову Q), i - 1,2; s = 0,..., 2ⁿ - 1.

Два N-слова и Q₂ будем называть N-противоположными, если для любой элементарной последовательности s переменных а₁,..., а_n имеет место

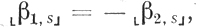
где а₁,..., а_n, β_i,s определяются так же, как выше для N-равенства.

Будем рассматривать далее только такие N-слова (а следовательно, и соответствующие формальные нейроны), в которые не входят элементарные слова, являющиеся N-противоположными.

Будем говорить, что нейрон A (а₁,..., а_n) возбуждается в данный момент времени t + i, i≥1, тогда и только тогда, когда

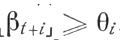
где θ_i - значение порога нейрона A в момент времени t + i, - входное слово, соответствующее всем возбужденным волокнам, которые соответствуют элементарной последовательности s_t n переменных, образованной входами в момент времени t; при построении β_t+i ребра, по которым сигнал не может прийти на тело в момент времени t + i, не учитываются, т. е. (W есть входное слово на Т_i-диаграмме, соответствующее элементарной последовательности s_t.

Аналогично определяется условие возбуждения - Т-возбуждение, не зависящее от времени прохождения сигналов по волокнам.

Будем говорить, что нейрон А (а₁,..., а_n) Т-возбуждается в данный момент времени t тогда и только тогда, когда

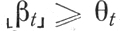
где θ_t - значение порога нейрона А в момент времени t_t - входное слово на Т-диаграмме, соответствующее элементарной последовательности s_t; s_t - элементарная последовательность, образованная входами нейрона в момент времени t.

Формальный нейрон в смысле Мак-Каллока возбуждается в момент времени t + 1 тогда и только тогда, когда он Т-возбуждается. Это утверждение следует из того, что для нейронов в смысле Мак-Каллока Т₁-диаграмма графически совпадает с Т-диаграммой.

Для описания функционирования формальных нейронов с n входами можно использовать диаграммы Венна n переменных аналогично случаю формальных нейронов в смысле Мак-Каллока (§ 2.1).

Диаграммы Венна формальных нейронов Мак-Каллока могут изменяться только при изменении значения порога нейронов, в то время как диаграммы Венна формальных нейронов в более общем смысле (предложенном в настоящем параграфе) могут изменяться как при изменении значения порогов нейронов, так и в зависимости от момента времени (используя условие возбуждения нейронов).

Для построения диаграммы Венна данного нейрона в момент времени t + i (i ≥ 0) при фиксированном значении порога используются T_i-диаграммы этого нейрона (i - 0 означает применение условия Т-возбуждения, а Т₀-диаграмма графически равна T-диаграмме).

Пример 2.15 (продолжение). Диаграммы Венна в различные моменты времени t + i нейрона на рис. 2.24 при θ = 5 имеют вид:

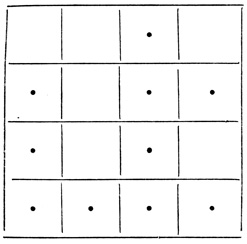
Таблица 2.1. Момент t

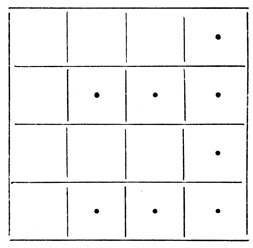
Таблица 2.2. Момент t + 2

Таблица 2.3. Момент t + 5

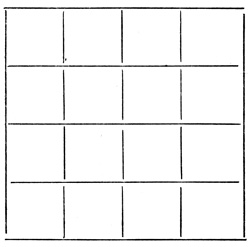
Таблица 2.4. Моменты t + 1, t + 3, t + 4, t + i, i ≥ 6

(Примечание. Используются таблицы Венна; ячейки обозначаются аналогично рис. 2.25.)

При θ = 2 диаграммы Венна этого нейрона имеют другой вид:

Таблица 2.5. Момент t

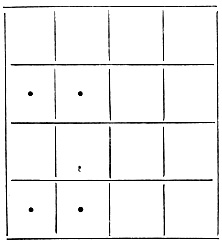
Таблица 2.6. Момент t + 1

Таблица 2.7. Момент t + 2

Таблица 2.8. Момент t + 4

Таблица 2.9. Момент t + 5

Таблица 2.10. Моменты t + 3, t + i (i≥6)

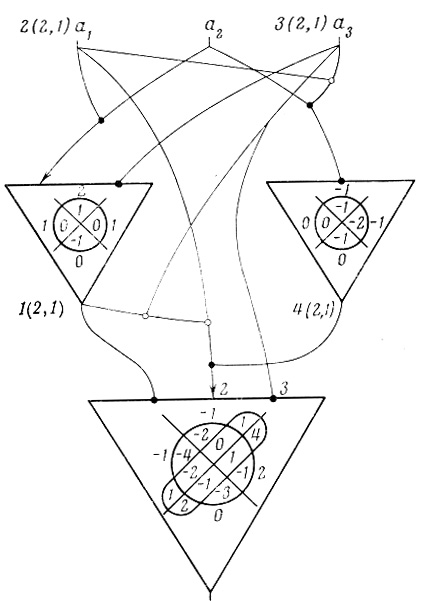
Рис. 2.26

Из введенных формальных нейронов можно строить сети аналогично тому, как это делалось в § 2,1. Аналогичным же образом определяются регулярные сети. Описание работы сетей формальных нейронов при фиксированных значениях порогов в случае Т-возбуждения можно осуществлять на сетях диаграмм Венна аналогично случаю нейронов Мак-Каллока. N-слова нейронов A_r,i, r - номер ранга в сети, i - номер нейрона в ранге, будем обозначать Q_r,i.

Пример 2.16. На рис. 2.26 приведена двухранговая сеть формальных нейронов. N-слова нейронов сети имеют вид:

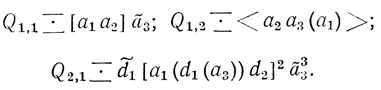
Нейроны первого ранга имеют по три входа а₁, а₂, а₃ (в порядке их расположения слева направо), входами нейрона второго ранга служат: 1-м - выход нейрона A_1,1, обозначается d₁ (на рисунке слева от входа стоит 1 (2,1)), 2-м - вход сети а₁ (на рисунке около а₁ поставлено 2 (2,1)), 3-м - вход сети а₃ (см. 3 (2,1)), 4-м - выход нейрона A_1,2, обозначается d₂ (см. 4 (2,1)).

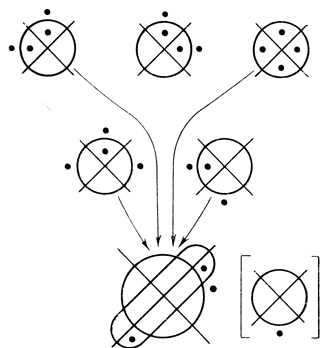
Рис. 2.27

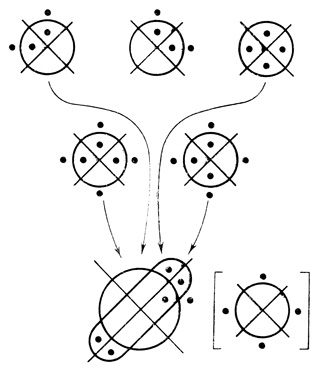
Рис. 2.28

Положив пороги нейрона А_1,1θ^1,1 = 1, нейрона А_1,2 θ^1,2 = 0 и нейрона A_2,1 θ^2,1 = 2, получим сеть диаграмм Венна (рис. 2.27). Уменьшая пороги θ^1,1 = 0, θ^1,2 = - 1, θ^2,1 = 1, получаем сеть на рис. 2.28. На обеих сетях результирующие диаграммы второго ранга совпадают с соответствующими операторами. Как исходная сеть нейронов, так и построенные сети диаграмм Венна не являются регулярными.