§ 2.3. Пороговые, порядковые и вероятностные диаграммы формальных нейронов

Определения.

1. Символ Венна n переменных, во всех ячейках которого, кроме нулевой ячейки, стоят произвольные целые числа (положительные, отрицательные и нуль), а в нулевой ячейке обязательно находится ноль, будем называть пороговой диаграммой n переменных.

Например, на телах нейронов А_1,1 и A_1,2 расположены пороговые диаграммы трех переменных, а на теле нейрона А_2,1 - пороговая диаграмма четырех переменных (рис. 2.26).

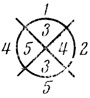
Рис. 2.29

2. Символ Венна n переменных, в каждой ячейке которого находится одно из чисел 1,2,..., m, m ≤ 2ⁿ (в разных ячейках может быть одно и то же число), будем называть порядковой диаграммой n переменных.

Например, на рис. 2.29 дана порядковая диаграмма трех переменных.

3. Вероятностные диаграммы n переменных определены в § 1.7.

Обозначения: D^θ - пороговая, D^π - порядковая диаграммы,

иногда в скобках справа указываем число переменных или сами переменные, например: D^π (n) или D^π (a₁,..., а_n) - порядковая диаграмма n переменных.

Записывать диаграммы будем не только с помощью символа Венна, но и в линейной форме: D^θ = (γ₀,......,γ_2ⁿ-1), где γ_j число в j-той ячейке пороговой диаграммы n переменных, j = 0,..., 2ⁿ - 1; D^π (α₀,.....,α_2^n-1)> где а j - число в j-той ячейке порядковой диаграммы n переменных, j = 0,..., 2ⁿ-1.

Например, D^θ (d₁, а₁, а₃, d₂) (0, 2, -3, -1, 2, 4,-1, 1, -1, 1, -4, -2, -1,1, -2, 0) - линейная запись пороговой диаграммы четырех переменных d₁, a₁, а₃, d₂ на теле нейрона А_2,1 (см. рис. 2.26, пример 2.16); D^π (5, 3, 2, 4, 4, 5, 1, 3) - линейная запись порядковой диаграммы трех переменных на рис. 2.29.

Установим соответствие между пороговыми, порядковыми и вероятностными диаграммами n переменных с одной стороны и формальными нейронами - с другой. Как и в § 2.2 при описании функционирования сетей диаграммами Венна, ограничимся T-возбуждением нейронов (не оговаривая это специально и понимая под возбуждением T-возбуждение), т. е. рассмотрим нейроны, не зависящие от времени,- выход есть функция только входа. О более общем случае, когда выход есть функция входа и времени, речь идет в параграфе, посвященном сетям формальных нейронов с обратными связями. Для понимания материала этого параграфа достаточно знания только сетей нейронов Мак-Каллока.

Пороговые диаграммы нейронов. Дан нейрон А (а₁,...,а_n). Построим символ Венна n переменных; в ячейке, соответствующей элементарной последовательности n переменных s, поставим число _[B_s], где B_s - входное слово в ячейке s диаграммы нейрона А s = 0,...,2ⁿ-1; полученную диаграмму будем называть пороговой диаграммой нейрона А (а₁,... ..., а_n).

Для нейронов Мак-Каллока числа _[B_s] равны разности между активированными возбуждающими и тормозящими волокнами (с учетом действия запретов) элементарной последовательности s.

Пороговая диаграмма нейрона характеризуется тем, что в нулевой ячейке символа Венна стоит нуль, а в остальных ячейках - целые числа (возможны и нули). Следовательно, пороговая диаграмма нейрона с n входами есть пороговая диаграмма n переменных.

Например, на телах нейронов рисунков 0.1, 2.1, 2.3, 2.5, 2.7, 2.26 расположены их пороговые диаграммы.

Отметим, что существуют нейроны, у которых не от всех входов идут волокна. Вход а, нейрона является фиктивным (т. е. от него не направлены волокна) тогда и только тогда, когда в каждой паре ячеек, соседних относительно входа а_i, его пороговой диаграммы находятся равные числа. Две ячейки символа Венна называем соседними относительно фигуры а_i, (входа a_i), если они отличаются друг от друга только тем, что одна из них принадлежит фигуре а_i, а другая не принадлежит фигуре а_i.

Например, у нейрона с пороговой диаграммой D^θ (0, 0, 2, 2, - 1, -1, 1, 1) третий вход фиктивен, нейрон фактически имеет два входа, его пороговую диаграмму можно записать D^θ (0, 2, -1, 1).

Если порог нейрона фиксирован, θ = θ₀, то по пороговой диаграмме этого нейрона можно однозначно определить как те элементарные последовательности, при которых нейрон возбуждается, так и те, при которых он не возбуждается: если γ_s ≥ θ₀, то нейрон возбуждается; если γ_s < θ_0[B_s], s = 0, 1,... 2ⁿ-1 (см. построение пороговой диаграммы нейрона).

Следовательно, пороговая диаграмма нейрона позволяет представить полную картину его функционирования. По пороговой диаграмме можно определить, во-первых, те значения его порога, при которых он всегда возбуждается (при любой из 2ⁿ элементарных последовательностей), во-вторых, те значения его порога, при которых он никогда не возбуждается, и, в-третьих, те значения его порога, при которых для одних элементарных последовательностей он возбуждается, а для других - не возбуждается; в первом случае соответствующая диаграмма Венна полна, во втором случае пуста, в третьем - имеет пустые ячейки и ячейки, содержащие точки.

Пример 2.14. (продолжение). Нейрон на рис. 0.1 возбуждается при любой элементарной последовательности, если θ ≤ -2. Если θ > 2, то при любой элементарной последовательности нейрон не возбуждается. При любом другом значении порога существуют как такие элементарные последовательности, при которых нейрон возбуждается, так и такие, при которых нейрон не возбуждается. Например, если θ = 0, то нейрон возбуждается, если его входы образуют одну из элементарных последовательностей: 0, 2, 5, 6-ю, и не возбуждается, если его входы образуют одну из элементарных последовательностей: 1,3, 4, 7-ю.

Порядковые диаграммы нейронов. На по-рядковой диаграмме n переменных можно указать порядок (отсюда название диаграммы) появления точек на диаграммах Венна n переменных, описывающих работу нейрона, при уменьшении значений порога, начиная с пустой диаграммы Венна.

Пример 2.1 (продолжение). Порядок появления точек на диаграммах D^τ (2) нейрона на рис. 2.1 при уменьшении значения порога, начиная с θ = 3, описывается на одной порядковой диаграмме двух переменных, D^π (2)(3, 2, 4, 1).

Пример 2.14 (продолжение). Порядковая диаграмма нейрона на рис. 0.1 имеет вид D^π (3) (3, 4, 2, 5, 5, 3, 1, 4).

Нейрон с n входами будем называть максимально невырожденным, если существует интервал изменения его порога длины 2ⁿ, в котором нейрон является невырожденным.

Пример 2.1 (продолжение). Нейрон на рис. 2.1 есть максимально невырожденный нейрон.

Если нейрон с n входами является максимально невырожденным, то все числа на его порядковой диаграмме попарно различны.

Действительно, предположим, что дан максимально невырожденный нейрон, т. е. задан интервал изменения его порога длины 2ⁿ, в котором нейрон является невырожденным, α₁ ≥ θ ≥ α₂, где α₁ и α₂ - целые числа, α₁ - α₂ = 2ⁿ. Тогда при θ = α₁ диаграмма Венна пуста (так как число ячеек диаграммы совпадает с длиной интервала, а нейрон является невырожденным); при уменьшении значения порога на единицу появляется первая и причем единственная точка на соответствующей диаграмме Венна - на символе Венна порядковой диаграммы в ячейке с номером, равным номеру ячейки, в которой на диаграмме Венна поставлена первая точка, пишем единицу; при дальнейшем уменьшении значения порога на единицу число точек на соответствующей диаграмме Венна увеличивается на единицу - на символе Венна порядковой диаграммы в ячейке с номером, равным номеру ячейки, в которой на диаграмме Венна поставлена новая точка, пишем число на единицу большее предыдущего; при θ = α₂ на символе Венна порядковой диаграммы в последней пустой ячейке будет написано число 2ⁿ. Следовательно, все ячейки порядковой диаграммы будут заполнены попарно различными числами 1,..., 2ⁿ.

На языке пороговых диаграмм n переменных условие максимальной не вырожденности имеет вид (обозначая числа пороговой диаграммы через γ_i, i = 0,....,2ⁿ-), γ_max ↔ max(γ₀,.....,γ_2ⁿ-1), γ_min ↔ min (γ₀,.....,γ_2ⁿ-1)

Нейрон с n входами будет максимально невырожденным тогда и ТОЛЬКО тогда, когда γ_max≤2ⁿ-1, γ_min≥1-2ⁿ, γ_max-γ_min=2ⁿ-1 и для любых i и j (i = 0,..., 2ⁿ-1; j = 0,..., 2ⁿ- 1) γ_i≠y^j при i≠j.

Пример 2.1 (продолжение). Вернемся к нейрону на рис. 2.1, n = 2, 2ⁿ - 1 = 3, γ_max = 2, γ_min = 1, γ_max-γ_min=3, γ_j≠γ_j при i ≠ j.

Порядковые и пороговые диаграммы различаются между собой прежде всего тем, что на пороговой диаграмме в нулевой ячейке обязательно находится ноль, а все числа на порядковой диаграмме больше нуля.

Вероятностные диаграммы нейронов. Функционирование сети формальных нейронов с входами a₁,......,а_n (в частности, одного нейрона) в зависимости от элементарных последовательностей переменных а₁,..., а_n (совпадающих с входами) можно описывать на вероятностных диаграммах n переменных.

Пусть для каждого нейрона сети задан свой интервал изменения порога. Тогда для данного выхода сети можно построить следующим образом вероятностную диаграмму n переменных:

единица, стоящая в s-той ячейке символа Венна n переменных, обозначает, что если входы сети образуют s-тую элементарную последовательность, то для любых значений порогов всех нейронов сети из указанных для них интервалов сеть возбуждается;

нуль, стоящий в t-той ячейке символа Венна n переменных, обозначает, что если входы сети образуют t-тую элементарную последовательность, то для любых значений порогов всех нейронов сети из указанных для них интервалов сеть не возбуждается;

буква р, стоящая в j-той ячейке символа Венна п переменных, обозначает, что если входы сети образуют j-тую элементарную последовательность, то существуют такие значения порогов у всех нейронов сети из указанных для них интервалов, что сеть возбуждается, и существуют такие значения порогов у всех нейронов сети из указанных для них интервалов, что сеть не возбуждается.

Описанную диаграмму будем называть результирующей вероятностной диаграммой сети при заданных интервалах изменения порогов.

Для каждой из возможных комбинаций значений порогов всех нейронов сети из указанных для них интервалов можно построить соответствующую сеть диаграмм Венна, результирующая диаграмма которой характеризует поведение сети (данного выхода) в зависимости от различных элементарных последовательностей переменных а₁,..., а_n при фиксированных значениях порогов, где переменные a₁,.....,а_n совпадают с различными входами сети. Обозначим все такие результирующие диаграммы через D^τ₁,.....,D^τ_r.

Тогда построение результирующей вероятностной диаграммы можно осуществлять аналогично тому, как это делалось для сетей вероятностных диаграмм в § 1.7:

если в s-той ячейке на каждой из диаграмм D^τ₁,..., D^τ_r есть точка, то в s-той ячейке символа Венна поставим единицу;

если i-тая ячейка на каждой из диаграмм D^τ₁,..., D^τ_r пуста, то в i-той ячейке символа Венна поставим нуль;

если в j-той ячейке на некоторых из диаграмм D^τ₁,..., D^τ_r (но не на всех) есть точки, а на всех остальных диаграммах в j-той ячейке пусто, то в j-той ячейке символа Венна поставим букву р.

В итоге получим результирующую вероятностную диаграмму работы сети нейронов для указанных интервалов изменения порогов.

Пример 2.15 (продолжение). Если порог нейрона на рис. 2.24 изменяется в интервале 5 < θ ≤ 10, то работа нейрона описывает

ся вероятностной диаграммой на рис. 1.53, в чем убедимся с помощью пороговой диаграммы этого нейрона D^θ (4) (0, -2, 5, 0, 5, 3, 7, 5, 7, 2, 12, 4, 9, 7, 11, 9), построив для каждого значения порога 0 свою диаграмму Венна:

В ячейках 10 и 14 на всех диаграммах есть точки, поэтому в ячейках 10 и 14 на рис. 1.53 находятся единицы. В ячейках 6, 8, 12, 13 и 15 в некоторых из диаграмм есть точки, например при θ = 6, а в некоторых - нет, например при θ = 10, поэтому в ячейках 6, 8, 12, 13 и 15 на рис. 1.53 расположены р. Все остальные ячейки на диаграммах Венна пусты, поэтому в соответствующих ячейках на рис. 1.53 стоят нули.

Пример 2.16 (продолжение). Возьмем сеть нейронов на рис. 2.26. Пусть 0 ≤ θ^1,1 ≤ 2, - 1 ≤ θ^1,2 ≤ 0, - 1 ≤θ^2,1 ≤ 2. Начертив сети диаграмм Венна для всех возможных комбинаций значений порогов из данных интервалов (например, на рис. 2.27 приведена сеть при θ^1,1 = 1, θ^1,2 = 0, θ^2,1 = 2), получим результирующую вероятностную диаграмму D^ρ (a₁, а₂, а₃) (р, р, 0, р, р, р, р).

С ростом числа нейронов в сети и с увеличением интервалов изменения порогов количество соответствующих сетей диаграмм Венна увеличивается.

Если интервалы изменения порогов нейронов сети состоят только из одного числа, то результирующая вероятностная диаграмма фактически совпадает с результатом работы соответствующей сети диаграмм Венна: точка заменяется единицей, в пустой ячейке ставится ноль.

Например, результирующую диаграмму сети на рис. 2.27 можно записать как вероятностную диаграмму D_ρ (1, 0, 0, 0, 0, 0, 0, 0).

Понятно, что для одного нейрона не обязательно перебирать все значения порога из данного интервала его изменения, достаточно взять наибольшее и наименьшее из значений, т. е. θ = ₁ и θ = θ_k (предполагая, что числа θ₁,..., θ_k - значения порога расположены в порядке убывания слева направо); во всех ячейках символа Венна, в которых на диаграмме D^τ₁ при θ = θ₁ есть точки, и только в них поставить по одной единице; во всех ячейках символа Венна, которые на диаграмме D^τ_k при θ = θ_k пусты, и только в них поставить по одному нулю; во всех оставшихся ячейках символа Венна поставить по одной букве p. Так, в примере 2.15 достаточно построить D^τ₁ при θ = 10 и D^τ₅ при 0 = 6.

Таким образом, для каждого нейрона сети при заданных интервалах изменения порогов можно построить соответствующую вероятностную диаграмму. В результате получается сеть G вероятностных диаграмм. Для нахождения результирующей вероятностной диаграммы полученной сети G можно воспользоваться одним из способов, предложенных в § 1.7. При этом способ, связанный с перебором всех возможных графически различных сетей диаграмм Венна, соответствующих G, часто требует большего перебора, чем описанный выше, в котором перебираются всевозможные комбинации порогов всех нейронов сети.

Пример 2.5 (продолжение). Пусть пороги нейронов сети на рис. 2.7 изменяются в интервалах

тогда соответствующая сеть вероятностных диаграмм имеет вид, показанный на рис. 2.30; общее число букв р в сети равно J = 14, т. е. число всех графически различных сетей диаграмм Венна равно 2¹⁴ = 16384; число всех различных комбинаций значений порогов равно, как нетрудно подсчитать, 540; число диаграмм сети, в которых есть по крайней мере одна буква р, равно J = 5, т. е. для построения результирующих диаграмм сети по первому способу из § 1,7 достаточно взять только 2⁵ = 32 сетей диаграмм Венна.

Сеть на рис. 2.30 регулярна, ее результирующие диаграммы можно построить по третьему способу из § 1.7 (в фигурных скобках результирующие диаграммы работы двух последних рангов сети).

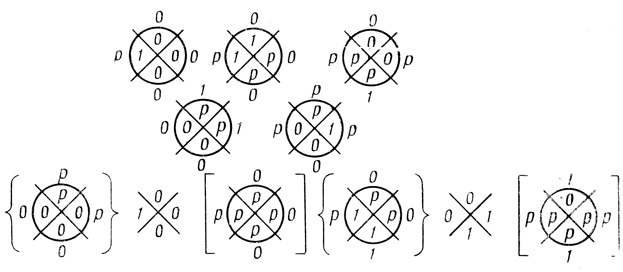
Рис. 2.30