§ 2.4. Сети формальных нейронов с обратными связями

Сеть формальных нейронов будем называть сетью с обратной связью, если в ней имеется по крайней мере один нейрон A_r,j, r ≥ 1, с входами (по крайней мере одним), которые совпадают с выходами нейронов (r + i)-го ранга, i ≥ 0. Нейроны в сети расположены, как и раньше, по рангам: A_r,i - i-тый нейрон (слева направо) r-того ранга (сверху вниз), d_r,i - выход нейрона A_r,j.

Элементами сети - формальными нейронами могут быть как нейроны в смысле Мак-Каллока, так и более общего вида в смысле § 2.2.

Примеры:

2.17. На рис. 2.31 дана одновыходная трехранговая сеть формальных нейронов с обратной связью: вторым входом нейрона А_2,1 и первым входом нейрона А_2,2 служит выход нейрона А_3,1. Элементами сети являются нейроны Мак-Каллока.

2.18. На рис. 2.32 второй вход нейрона А_2,1 совпадает с его выходом, а входы нейрона А_1,3 совпадают соответственно с выходами нейронов A_2,2, A_3,1 и A_2,1. Заметим, что первый и третий входы нейрона А_3,1 одинаковы - выход нейрона A_2,1.

2.19. Сеть с двумя выходами показана на рис. 2.33. Нейрон A_1,1 имеет четыре входа: первый вход - d_2,1 (выход первого нейрона второго ранга), второй, третий и четвертый - входы сети соответственно а₁, а₂ и а₃, А_1,3 и А_2,2 - нейроны Мак-Каллока. На теле нейрона А_1,1 оканчивается тормозящее волокно с двумя ярусами, а нейроны А_1,2 и А_2,1 имеют одноярусные волокна.

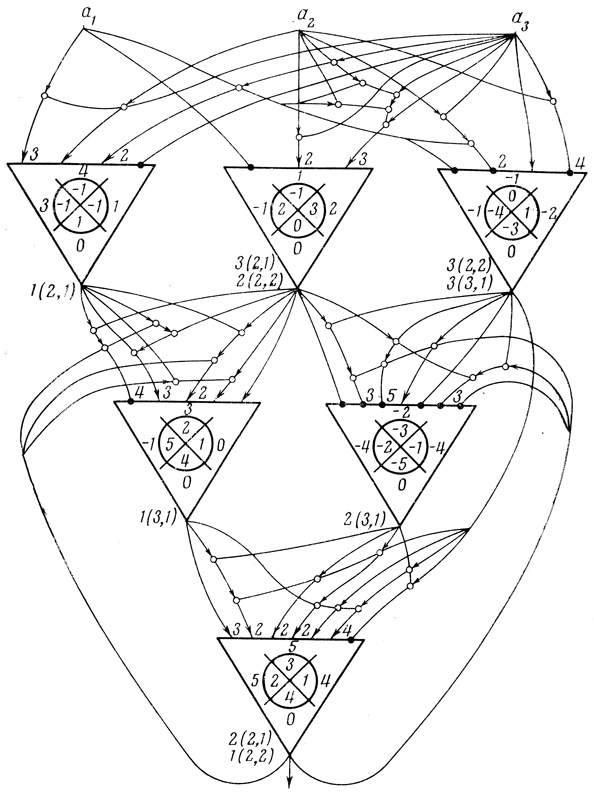
Рис. 2.31

Рассматривать работу сетей формальных нейронов (как с обратной связью, так и без нее) будем в различные моменты времени, предполагая, что возбуждение нейрона зависит от времени прохождения сигналов по волокнам, т. е. будем исследовать условие возбуждения (а не Т-возбуждения) нейронов.

Возбуждение нейрона при фиксированном значении его порога зависит только от веса входного слова, соответствующего всем возбужденным (активированным) волокнам нейрона в рассматриваемый момент времени t + i, i > 0, т. е. в соответствии с определением в § 2.2 нейрон А (а₁,..., а_N) возбуждается в данный момент времени t + i, i > 0, тогда и только тогда, когда _[B_t,i] ≥ θ_i, где θ_i - значение порога нейрона А в момент времени t + i; B_t,i - входное слово на T_i-диаграмме, соответствующее s_t; s_t - элементарная последовательность, образованная входами a₁,...,a_n нейрона А в момент времени t.

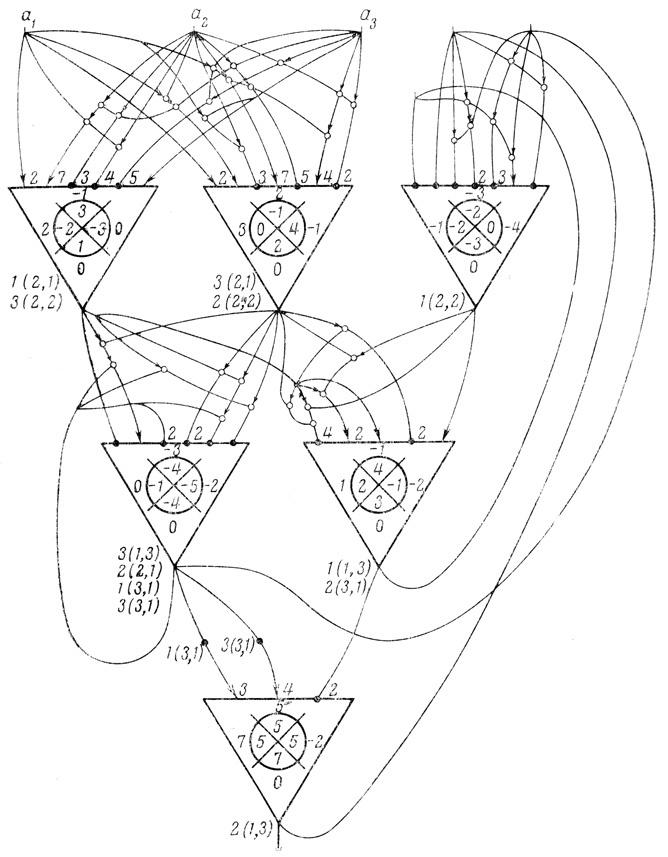
Рис. 2.32

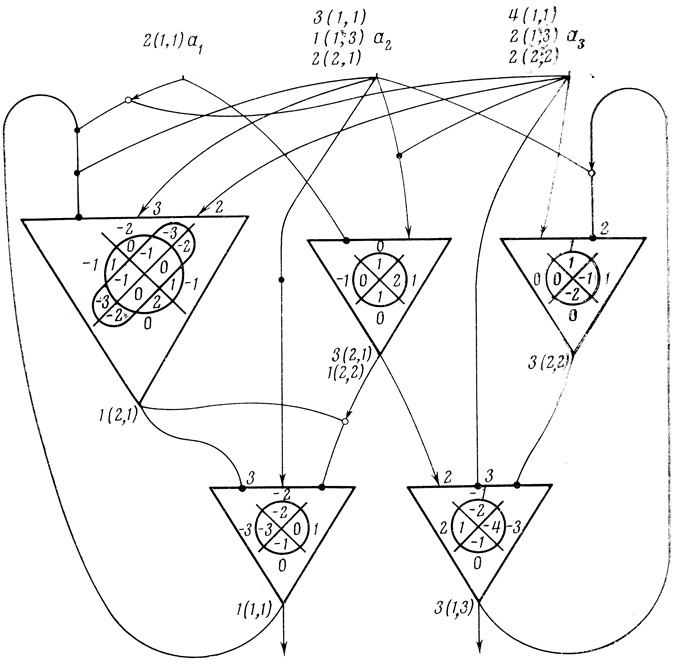
Рис. 2.33

Каждой элементарной последовательности s_t переменных а₁,...,а_n соответствует определенное входное слово B_t,i на T_i-диаграмме; например, последовательности 0...0 (n нулей) соответствует пустое слово. Числа _[B_t,i], соответствующие всем 2ⁿ графически различным элементарным последовательностям переменных a₁,..., а_n, образуют пороговую диаграмму n переменных. Такие пороговые диаграммы будем называть Т_i-пороговыми диаграммами.

Таким образом, каждой Т_i-диаграмме нейрона соответствует определенная T_i-пороговая диаграмма. Для общности иногда пороговую диаграмму нейрона (она соответствует его T-диаграмме) будем называть T-пороговой или Т₀-пороговой диаграммой, при этом иногда будем говорить, что она соответствует моменту времени t. В примерах 2.17-2.19 на телах нейронов расположены их Т-пороговые диаграммы. Если бы первый и третий входы нейрона А_3,1 на рис. 2.32 не совпадали, то его T-пороговой диаграммой была бы диаграмма (0, 4, - 2, 2, 3, 7, 1,5) - запись в линейной форме.

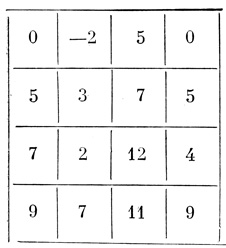
Таблица 2.11. Момент t, T₀-пороговая диаграмма

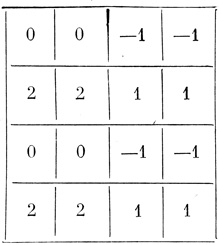
Таблица 2.12. Момент t + 1, T₁-пороговая диаграмма

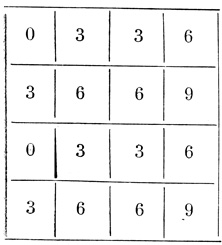
Таблица 2.13. Момент t + 2, Т₂-пороговая диаграмма

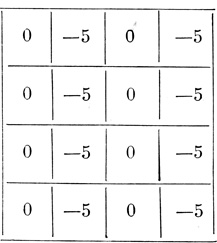
Таблица 2.14. Момент t + 3, T₃-пороговая диаграмма

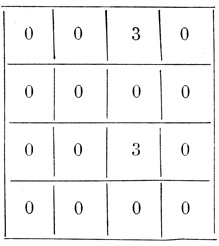
Таблица 2.15. Момент t + 4, T₄-пороговая диаграмма

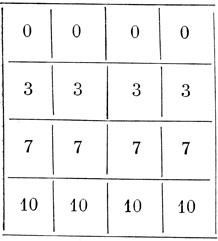
Таблица 2.16. Момент t + 5, Т₅-пороговая диаграмма

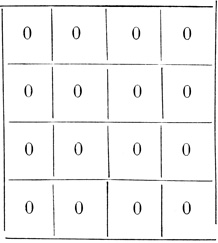
Таблица 2.17. Момент t + i, T-пороговая диаграмма, i≥6

(Примечание. При построении символа Венна используются таблицы, ячейки обозначаются аналогично рис. 2.25.)

Пример 2.15 (продолжение). T_i-пороговые диаграммы нейрона на рис. 2.24, соответствующие различным моментам времени t + i, показаны в табл. 2.11-2.17.

Сети пороговых диаграмм. Построение сетей по-роговых диаграмм осуществляется так же, как и сетей вероятностных диаграмм. При этом могут строиться как регулярные сети пороговых диаграмм, так и сети более сложного вида, в частности сети с обратной связью.

Различие состоит только в том, что перед первым рангом указываются все входы сети, т. е. входами пороговой сети являются не диаграммы первого ранга (как в сетях вероятностных диаграмм), а буквы a₁,.....,а_n (аналогично сетям формальных нейронов). Среди

диаграмм первого ранга могут встречаться диаграммы, не связанные с входами сети.

Примеры сетей пороговых диаграмм приведены на рис. 2.34-2.36.

Заметим, что по построению сети пороговых диаграмм похожи на сети формальных нейронов, у которых от каждого входа нейрона может быть проведено только одно возбуждающее волокно, а вместо тела расположена пороговая диаграмма.

Пусть дана сеть G формальных нейронов с входами а₁,..., а_n.

В момент времени t (начальный момент) входы сети образуют определенную элементарную последовательность - одну из 2ⁿ возможных графически различных элементарных последовательностей.

Поведение сети G (возбуждение или не возбуждение ее выходов) будем изучать в моменты времени t + i, i > 0. За основу возьмем поведение сети в момент времени t и будем предполагать, что сеть, начиная с момента времени t, полностью изолирована. Изучение начнем с построения сетей T_i-пороговых диаграмм.

В момент времени t + 1 на тела некоторых нейронов могут поступать сигналы как от возбужденных входов сети, так и от возбужденных в момент времени t нейронов. Тем самым для каждого нейрона сети может быть построена T_i-диаграмма, а следовательно, и T_i-пороговая диаграмма.

Таким образом, получается сеть T_i-пороговых диаграмм, соответствующая сети G формальных нейронов.

Сеть Т_i-пороговых диаграмм (i> 1), соответствующая G в момент времени t + i, строится аналогично сети T_i-пороговых диаграмм. При построении T_i-диаграмм учитываются сигналы, поступающие от возбужденных входов сети и от возбужденных в моменты времени t + j (0 ≤ j < i) нейронов.

Определение. Будем говорить, что сеть G формальных нейронов образует цикл пороговых диаграмм, если сети T_i-пороговых диаграмм, соответствующие сети G, периодически (с периодом μ) повторяются, начиная с некоторого момента времени; этот момент времени будем называть началом цикла пороговых диаграмм, а число μ - длиной цикла.

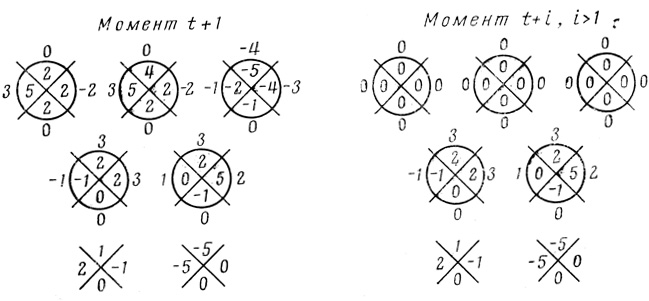
Рис. 2.34

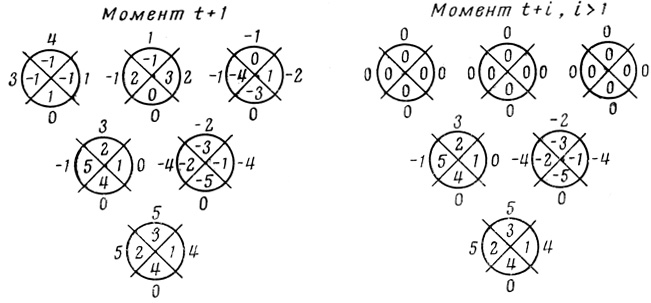
Рис. 2.35

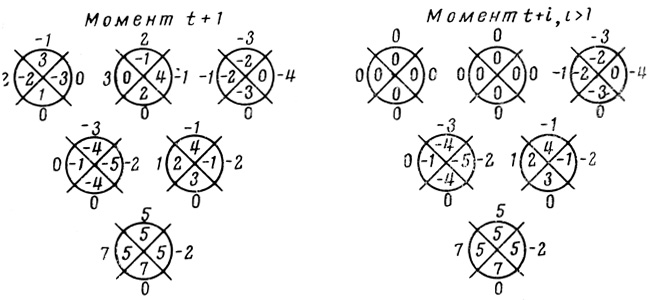
Рис. 2.36

Примеры:

2.5. (продолжение). Регулярная сеть формальных нейронов на рис. 2.7 образует цикл пороговых диаграмм длины μ = 1; началом цикла является момент t + 2 (рис. 2.34).

2.17. (продолжение). Сети T_i-пороговых диаграмм, соответствующие сети формальных нейронов рис. 2.31, приведены на рис. 2.35.

2.18. (продолжение). На рис. 2.36 даны пороговые диаграммы нейронов сети рис. 2.32.

2.20. В предыдущих примерах строились сети пороговых диаграмм, соответствующие сетям формальных нейронов, волокна которых не имеют ярусов.

Займемся сетью с обратной связью, содержащей более сложные волокна (§ 2.2), но состоящей только из одного нейрона (рис. 2.37; T_i-пороговые диаграммы сетей из большего числа нейронов с волокнами, имеющими ярусы, в настоящей работе не разбираются).

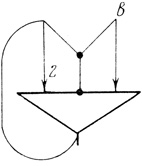
Рис. 2.37

Первый вход сети совпадает с ее выходом. Число волокон сети равно трем: первое - возбуждающее волокно с весом 2 начинается на первом входе и оканчивается на теле нейрона; второе - одноярусное, тормозящее волокно, его вершина в первом ярусе связана с обоими входами; третье - возбуждающее волокно, начинающееся на втором входе.

В момент времени t могут быть возбуждены оба входа (активность первого входа - выхода сети зависит от предшествующих моментов времени).

В момент времени t + 1 информация на тело нейрона может поступать только по первому и третьему волокнам. Следовательно пороговая диаграмма нейрона имеет вид D^θ_t+1 (0, 1, 2, 3).

В момент времени t + 2 возможны два случая:

1) функционирование первого входа определяется в момент t, тогда сигналы на тело нейрона могут поступать только по второму волокну и D^θ_t+2,1 (0, -1, -1, -2);

2) поведение первого входа определяется в момент времени t + 1, тогда импульсы на тело нейрона могут поступать по первому и второму волокнам (по второму волокну может проходить сигнал только от второго входа, который независим: он может быть возбужден, как принято в работе, только в момент времени t): D^θ_t+2,2(2)(0, -1. 2, 1).

В момент времени t + 3 возможны три случая:

1) поведение первого входа определяется в момент t, тогда сигналы на тело нейрона не поступают, т. е. D^τ_t+3,1 (2) (0, 0, 0, 0);

2) поведение первого входа определяется в момент времени t +1, следовательно, сигналы на тело нейрона могут проходить только от первого входа второго волокна: D^υ_t+3,2 (2) (0, 0, -1, -1);

3) поведение первого входа определяется в момент времени t+2, поэтому информация на тело нейрона может поступать только по первому волокну: D^τ_t+3,3 (0, 0, 2, 2). Нетрудно убедиться, что, начиная с момента времени t + 3, T_i-пороговые диаграммы будут повторяться (при этом число диаграмм, содержащих только нули, будет увеличиваться).

При разборе последнего примера предполагалась зависимость поведения нейрона от работы его входов (совпадающих с выходами каких-либо нейронов) во все предшествующие моменты времени, начиная с момента t. Само собой разумеется, что это предположение не является единственным; можно, например, ограничиться случаем, когда функционирование нейрона Зависит только от состояния входов в предыдущий такт времени (речь идет, как и выше, о входах, совпадающих с выходами каких-либо нейронов; независимые входы, т. е. входы сети, могут возбуждаться только в момент времени t).

В каждый данный момент времени t + i (i > 1) по T_i-пороговой диаграмме нейрона можно построить при указанном интервале изменения порога нейрона вероятностную диаграмму (§ 2.3).

Следовательно, по сети G формальных нейронов с заданными интервалами изменения порогов всех нейронов в каждый данный момент времени t + i (i > 1) Сложно построить сеть вероятностных диаграмм, результирующие диаграммы которой и описывают функционирование сети G (способы построения результирующих диаграмм см. в § 1.7)

Пример 2.17 (продолжение). Положим для нейронов сети на рис. 2.31 θ^1,11 = 1, θ^1,2 = 1, θ^1,3 = -1,1 ≤ θ^2,1 ≤ 4, -3 ≤ θ^2,2 ≤ - 1,1, 1 ≤ θ^3,1 ≤ 4. Получим в момент времени t + 1, используя T_i-пороговые диаграммы рис. 2.35, сеть вероятностных диаграмм, приведенную на рис. 1.55.