Глава 3. Синтез формальных нейронов

§ 3.1. Аналитические выражения формальных нейронов

В главе 2 изложены способы описания функционирования формальных нейронов и сетей из них диаграммами Венна в исчислении высказываний порядковыми, пороговыми и вероятностными диаграммами n переменных.

Обратной задачей является построение формальных нейронов по известным функциям (условиям) их работы. Например, на языке пороговых диаграмм задача формулируется следующим образом.

Дана пороговая диаграмма n переменных D^θ (n).

Требуется синтезировать такой формальный нейрон, пороговой диаграммой которого будет диаграмма D^θ (n).

Решать задачу будем прежде всего для формальных нейронов, описанных в § 0.3. Предварительно введем аналитические выражения таких формальных нейронов.

Аналитическим выражением Ω_n формального нейрона А (n) будем называть сумму, каждое из слагаемых которой соответствует только одной из ветвей нейрона (с указанием условий включения ее в j-тую входную последовательность). Для построения аналитического выражения последовательно просматриваются все ветви, оканчивающиеся на теле нейрона (вместе со всеми связанными с ними запретами):

1) для ветви входа а_i без запретов слагаемое имеет вид H_iа_i;

2) для ветви входа а_i с одним запретом от входа а_j слагаемое имеет вид H_i(j) а_i (1 - a_j);

3) для ветви входа а_i с двумя запретами от входов а_j и a_k слагаемое имеет вид H_i(j,k) а_i (1 - a_j)(1 - a_k);

4) для ветви входа а_i с одним запретом от входа а_j, в свою очередь запрещаемым входом a_k, слагаемое имеет вид H_i,(j,(k))a_i(1 - a_j⋅(1 - a_k));

5) слагаемые, соответствующие всем остальным ветвям, определяются аналогично.

В качестве примера приведем аналитическое выражение для трех входового нейрона (с использованием волокон типа "запрет запрета"):

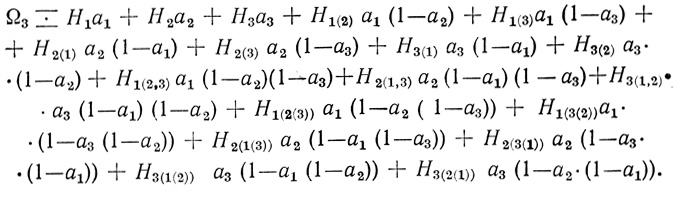(3.1)

В аналитическом выражении (3.1) не учтены все возможные комбинации "запрета запретов", но оно позволяет (как будет показано ниже) уменьшить общее число необходимых волокон нейрона.

Коэффициенты слагаемых аналитических выражений, записанные в виде букв с индексами, представляют собой веса ветвей. Индексы позволяют полностью определить соответствующую ветвь нейрона.

Например, H_{2(1(3(2))(4))} = -5 означает, что от входа а₂ на тело направлено тормозящее волокно α с весом 5 (тормозящее потому, что значение коэффициента отрицательно; от 2-го входа потому, что индекс начинается двойкой), на волокне а оканчивается запрещающее волокно от входа ах (так как за отмеченным числом 2 в индексе следует вполне круглое слово, основа которого начинается единицей), на запрещающем волокнеах оканчиваются запрещающие волокна α₂, аз соответственно от входов α₃, α₄, наконец, на волокне α₂ от входа α₃ оканчивается запрещающее волокно от входа α₃ (рис. 3.1).

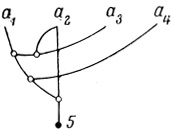
Рис. 3.1

Между индексом коэффициента и частью слагаемого после коэффициента устанавливается взаимно однозначное соответствие. Так, после коэффициента H_{2(1(3(2))(4))} в соответствующем слагаемом аналитического выражения пишется a₂ (1-a₁ (1-a₃ (1 - a₂)) (1-a₄)).

Аналитические выражения можно определять независимо от формальных нейронов. Например, аналитические выражения можно вводить через N-слова, в построении которых не участвует пункт 3 определения, т. е. через такие N-слова, в которые не входят слова вида N₁ и N̄₁ (§ 2.2).

С помощью аналитических выражений можно находить пороговые диаграммы формальных нейронов.

Число γ_j пороговой диаграммы нейрона А (а₁,..., а_n), соответствующее данной входной (элементарной) последовательности j, равно числу, которое получается после подстановки в аналитическое выражение нейрона вместо переменных а_`,..., а_n их значений β₁,..., β_n из последовательности, j, jβ₁,....,β_n, где β_i1 обозначает возбужденность входа a_i, β_i0 - не возбужденность входа a_k.

Если результат подстановки β₁,.....,β_n вместо а₁,..., а_n в Ω_n обозначить

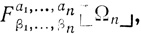
то

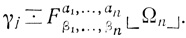(3.2)

Пример 2.14 (продолжение). а₁ - 3а₁ (1 - а₂) (1 - а₃) - а₂ + 2а₂ (1 - а₃) - а₃ - аналитическое выражение нейрона, изображенного на рис. 0.1; подсчитаем числа на пороговой диаграмме (при нумерации ячеек воспользуемся двоичной системой):

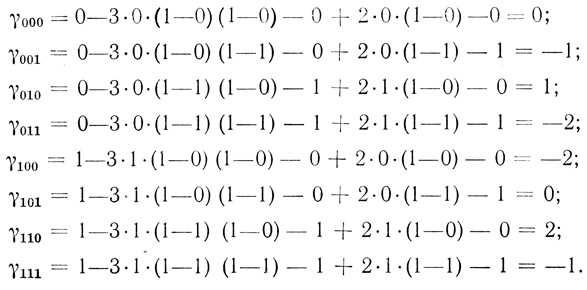
Аналитические выражения с неопределенными коэффициентами, составленные из букв а₁,..., а_n, можно использовать при синтезе формальных нейронов с входами а₁,..., а_n.

Например, пусть дана пороговая диаграмма D^θ (n). Выберем некоторое аналитическое выражение Ω_n. Тогда решение задачи синтеза в силу соответствия между нейронами и аналитическими выражениями сводится к нахождению значений коэффициентов последних. Для определения значений коэффициентов строится система 2ⁿ - 1 линейных алгебраических уравнений - результат подстановки в аналитическое выражение Qn вместо переменных a₁,...,a_n их значений β₁,...,β_n (из рассматриваемой входной последовательности). есть уравнение, неизвестными которого являются коэффициенты выражения Ω_n.

Предлагаемый метод проектирования нейронов в работе иллюстрируется при n = 2, 3, 4. При этом используются аналитические выражения из следующих двух классов.

В первый класс включим аналитические выражения, которым соответствуют нейроны без волокон типа "запрет запрета". Число всех возможных различных слагаемых в аналитическом выражении Ω_n равно n⋅2^n-1.

Другой способ синтеза нейронов этого класса описывается, например, в [16, 26]. Однако в этих работах решение усложняется вспомогательными диаграммами, которые строятся для каждого входа нейрона и для которых существенно, что нет волокон типа "запрет запрета". Аналитические выражения этого класса введены и использованы для синтеза нейронов С. Л. Никогосовым.

При n = 2 аналитическое выражение имеет вид

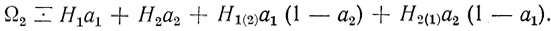(3.3)

Скобки в индексах коэффициентов в (3.3) можно опускать при условии, что вторая цифра соответствует запрещающему волокну; тогда (3.3) переписывается в виде

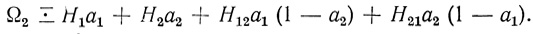(3.4)

При n = 3

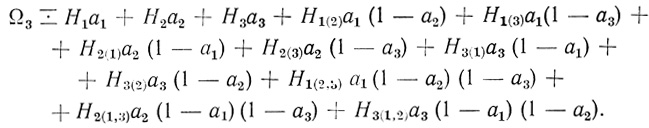(3.5)

При n = 4

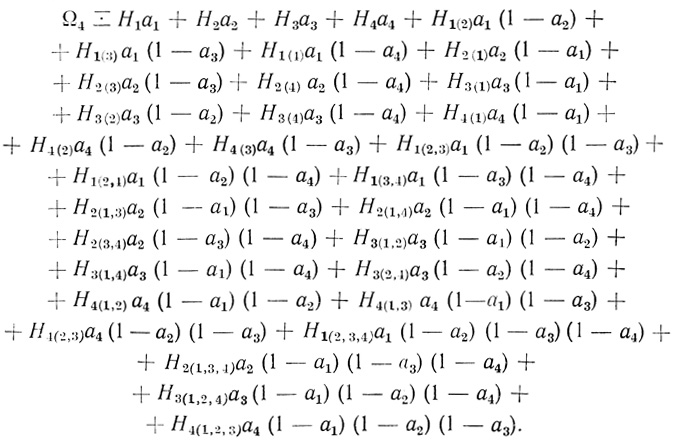(3.6)

Аналогично случаю n = 2 при n = 3, 4 скобки и запятые в индексах коэффициентов можно не писать. Например,

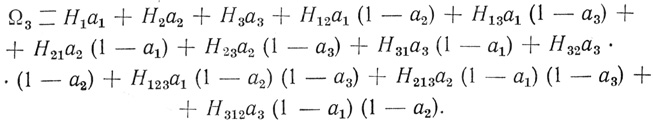(3.7)

Во втором классе аналитических выражений число членов в выражениях увеличивается по сравнению с первым классом; добавляются члены, соответствующие волокнам типа "запрет запрета". Аналитический выражения этого класса будем обозначать Ω'_n. Для примера возьмем аналитическое выражение (3.1), перепишем его, опуская (для сокращения) внутренние пары скобок и запятые в индексах коэффициентов:

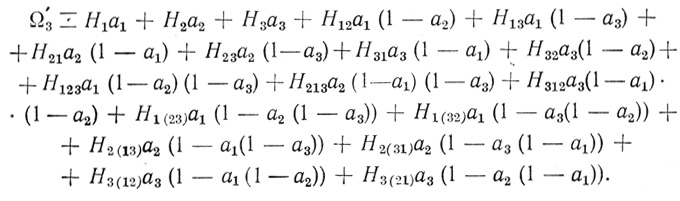(3.8)