§ 3.2. Построение формальных нейронов по пороговым диаграммам n переменных

Дана пороговая диаграмма D^θ (n).

Требуется построить формальный нейрон, пороговой диаграммой которого является D^θ (n).

При n = 3

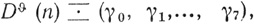
где γ₀ = 0; γ₁ - целое число, i = 1,..., 7.

1. Рассмотрим аналитические выражения первого класса, содержащие n⋅2^n-1 различных коэффициентов.

Пусть Ω_n - аналитическое выражение первого класса. Перебирая все различные; входные последовательности и подставляя их члены в получим систему 2ⁿ-1 линейных алгебраических уравнений с n⋅2^n-1 неизвестными и одно тождество 0 = 0 (соответствующее входной последовательности из n нулей - 0...0).

При n = 3 из (3.7) получается система 7 уравнений с 12 неизвестными:

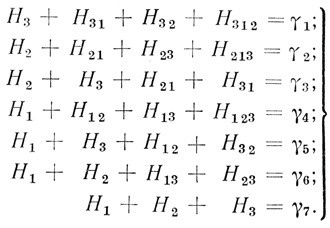(3.9)

Матрица системы (3.9) имеет вид:

(3.10)

(столбцы соответствуют переменным в следующем порядке: H₁, H₁₂ H₁₃, H₁₂₃, H₂, H₂₁, H₂₃, H₂₁₃, H₃, H₃₁, H₃₂, H₃₁₂).

Для каждой t-той строки матрицы (3.10) можно найти столбец, у которого в t-той строке стоит единица (отмечаем ее кружочком), а во всех ниже стоящих строчках - ноль. Поэтому ранг системы (3.9) равен 7 - числу уравнений системы (аналогичное предложение верно для любого n - ранг системы равен 2ⁿ-1).

Выбирая за свободные переменные H₂, H₃, H₂₃, H₃₁, H₃₂ (в столбцах которых нет отмеченных кружками единиц), получим

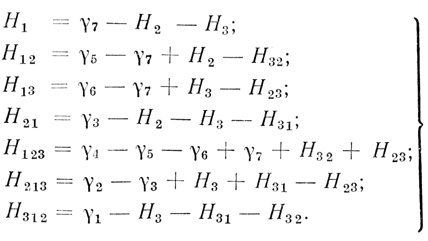(3.11)

Придавая свободным переменным произвольные целочисленные значения, определим все коэффициенты в Ω_n. По значениям коэффициентов выражения Ω_n однозначно строится формальный нейрон, пороговой диаграммой которого будет исходная диаграмма D^θ(n).

Пример 3.1. Дана пороговая диаграмма D^θ (3) (0, 1, -2, 3, 1, -3, 2, 4).

В силу (3.11) получаем

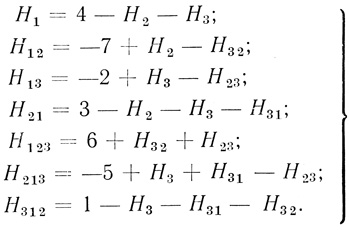
Положим H₂₃ = -5, H₃₂ = 1, H₃ = 0, H₃₁ = 0, H₂ = 3, вычисляем H₃₁₂ = 0, H₂₁ = 0, H₂₁₃ = 0, H₁ = 1, H₁₃ = 3, H₁₂ = -5, H₁₂₃ = 2. По найденным значениям коэффициентов построим нейрон с общим числом волокон W = 38 (рис. 3.2).

2. По данной пороговой диаграмме D^θ(n) конструируем нейрон, который может содержать волокна типа "запрет запрета".

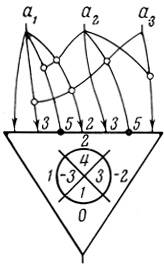
Рис. 3.2

Задача решается аналогично предыдущему случаю, различие состоит только в том, что по аналитическому выражению второго класса Ω_n получаем систему 2ⁿ-1 линейных алгебраических уравнений с большим числом неизвестных.

При n = 3 из (3.8) определяется система 7 уравнений с 18 неизвестными:

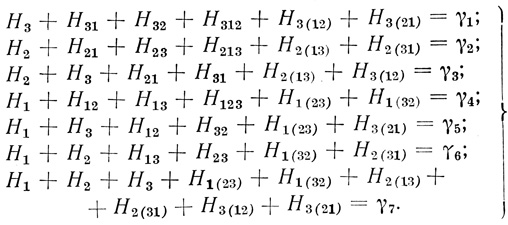(3.12)

Если положить H₁₍₂₃₎ = H₁₍₃₂₎; = H₂₍₁₃₎ = H₂₍₃₁₎ = H₃₍₁₂₎ = H₃₍₂₁₎ = 0, то система (3.12) преобразуется в систему (3.9). Матрица системы (3.12) имеет вид:

(3 13)

Матрица (3.13) отличается от матрицы (3.10) только последними шестью столбцами, которые соответствуют переменным H₁₍₂₃₎, H₁₍₃₂₎, H₂₍₁₃₎, H₂₍₃₁₎, H₃₍₁₂₎, Н₃₍₂₁₎б т. е. ранги матриц (3.13) и (3.10) равны.

Выбирая за свободные переменные Н₁, Н₁₂, H₁₃, H₂, H₂₁, H₃, H₁₍₂₃₎, H₁₍₃₂₎, H₂₍₁₃₎, H₂₍₃₁₎, H₃₍₁₂₎ (в столбцах которых нет отмеченных кружками единиц), получим

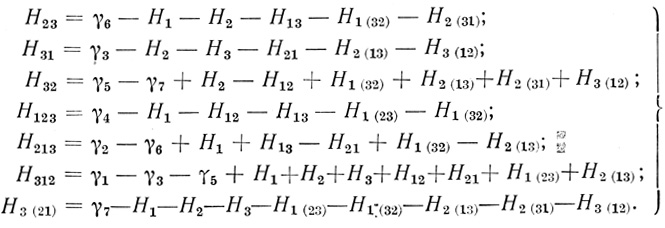(3.14)

Придавая, как и в (3.11), свободным переменным произвольные целочисленные значения, определим все коэффициенты в Ω'_n, по которым однозначно можно построить нейрон, пороговой диаграммой которого является исходная диаграмма Dθ (n). Найденный нейрон может содержать волокна типа "запрет запрета".

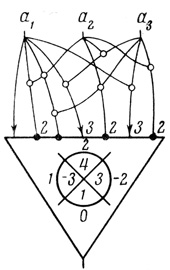
Рис. 3.3

Пример 3.1 (продолжение). Подставляя в (3.14) значения γ_j из данной D^θ(3) (см. начало примера), получаем

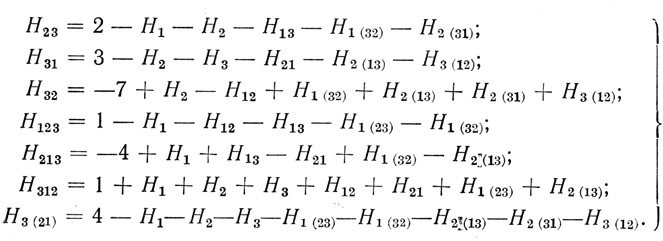
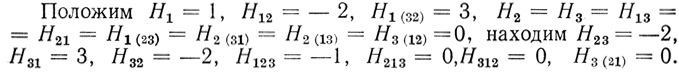
По значениям коэффициентов начертим нейрон (рис. 3.3), общее число волокон W = 31.