§ 3.4. Синтез формальных нейронов с минимальным числом волокон на ЭЦВМ
А. Суммарное число волокон
Из общего аналитического выражения Ω для каждой из ячеек пороговой диаграммы Dθ, за исключением нулевой, может быть составлено одно уравнение; таким образом, для пороговой диаграммы n входов можно составить k = 2n - 1 уравнений. В этих k уравнениях в общем случае содержится m = С1n + 2С2n + ... + kCkn +....+ nCnn = nΣk=0 kCkn переменных вида Нi.
В [16] показано, что m = n2n-1. Это вытекает из следующих соображений. Пусть
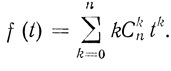 (3.15)
(3.15)Тогда
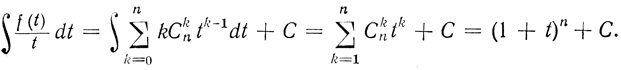 (3.16)
(3.16) Взяв производную от обеих частей равенства (3.16), получаем
f(t)/t = n(1+)n-1
Положив в этой формуле t = 1, получим
f (1) = n2n-1
Одновременно из (3.15) следует, что при t = 1
f(1) = nΣk=0 kCkn
Отсюда число всех переменных в системе уравнений, полученной из аналитического выражения для произвольного количества п входов, будет
m = n⋅2n-1, (3.17)
Таким образом, число переменных превышает число уравнений на величину I:
1 = m - k = n⋅2n-1 - 2n + 1. (3.18)
Иначе говоря, любыми l переменными можно варьировать произвольно, и определяя по ним остальные k = 2n - 1 переменных, синтезировать нейрон. Задача сводится к тому, чтобы l переменных
выбрать в соответствии с тем или иным критерием оптимальности нейрона.
Для синтеза нейронов с оптимальными параметрами Ŵ и V̂ необходимо определить общее число волокон и ветвей, выразив их через l независимых переменных.
Для составления формулы, выражающей общее количество волокон W, необходимо учесть, что величины Hij, имеющие двойной индекс, дают и двойное количество волокон, так как они представляют собой то количество волокон, которое идет от входа ai и запрещается входом aj вполне очевидно, что если от данного входа идет некоторое количество волокон Hij, которые запрещаются другим входом, то запрещающих волокон должно быть точно столько же; кроме того, необходимо учесть, что величина Нij может быть как положительной (возбуждающие волокна), так и отрицательной (тормозящие волокна); нас же интересует абсолютная величина количества волокон, и поэтому волокна всех ветвей типа Hij будем учитывать в виде 2|Hij|. Аналогично этому коэффициенты для любых других величин Hi должны быть равны количеству индексов при этих величинах. Так, очевидно, при абсолютной величине параметра Hijk должен быть коэффициент 3, так как эта величина представляет собой не только число волокон, принадлежащих входу ai, но также и равные последнему количества волокон, запрещающие эту ветвь входами аj и аk.
Основываясь на этих соображениях и на определении аналитических выражений, для случая n = 3 можно написать
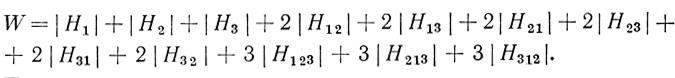 (3.19)
(3.19) При том же числе входов n = 3, но использовании волокон типа "запрет запрета" общее число волокон составит величину
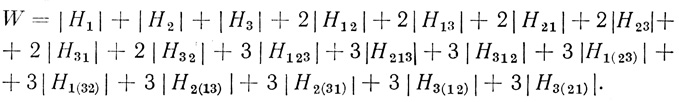 (3.20)
(3.20) Аналогично этому при n = 4 имеем
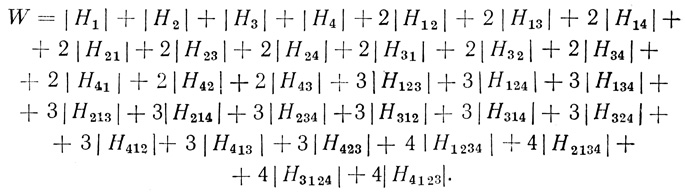
Теперь необходимо выбрать l независимых переменных и через них выразить остальные k параметров.
Для случая n = 3 в § 3.2 были выбраны следующие l = 3⋅23-1 - 23 + 1 = 5 свободных переменных, которые обозначим через вектор X с компонентами (x1,...,xj,..., xl):
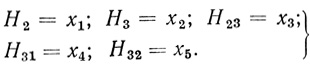 (3.22)
(3.22)Кроме этого, обозначим
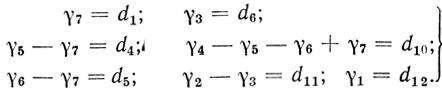 (3.23)
(3.23)Свободные переменные в системе (3.9) выбирались так, чтобы все 2n - 1 уравнений с остальными 2n - 1 переменными были линейно независимы. Проверка независимости уравнений показана в § 3.2.
Таким образом, система уравнений (3.9) может быть решена относительно связанных переменных, которые при этом окажутся выраженными через свободные X. С учетом принятых обозначений и (3.22), (3.23) в результате решения системы получим:
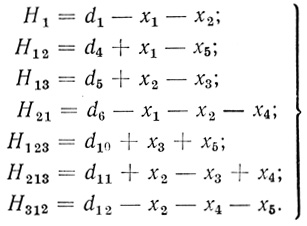 (3.24)
(3.24)Подставив (3.24) в (3.19), с учетом принятых обозначений для Hi получим окончательную формулу для общего числа волокон при n = 3.
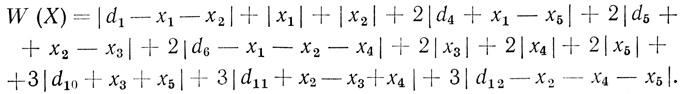 (3.25)
(3.25)Таким образом, общее число волокон оказывается зависящим от логики нейрона (через величины di = di (γi)) и от выбора свободных переменных X.
Аналогичным путем найдем величину W для n = 3 при условии использования волокон типа "запрет запрета". Воспользуемся для этого аналитическим выражением (3.1) и системой уравнений (3.12). Выбранные в качестве свободных 11 переменных (в этом случае в 7 уравнениях имеется 18 переменных) обозначим через набор X:
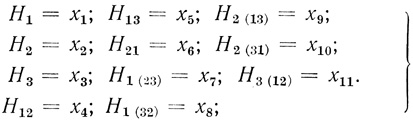 (3.26)
(3.26)Кроме этого, обозначим:
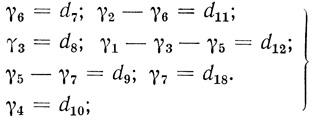 (3.27)
(3.27)Решив систему уравнений (3.12) относительно несвободных переменных с учетом (3.26) и (3.27), получим:
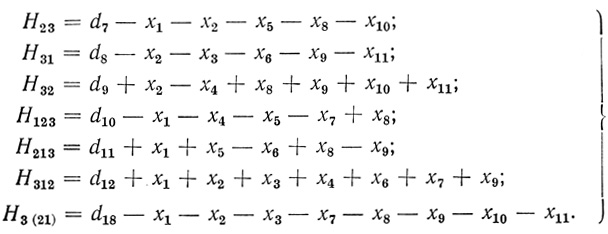 (3.28)
(3.28)Подставив (3.28) в (3.20) с учетом (3.26), получим для этого случая формулу для общего числа волокон:
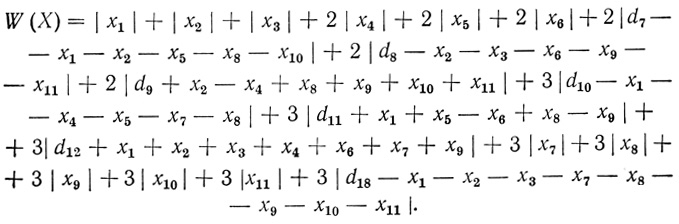 (3.29)
(3.29)Практически часто встречается потребность в синтезе четырехвходовых нейронов. Поэтому выведем формулу для случая n = 4. Составим для этого случая аналитическое выражение
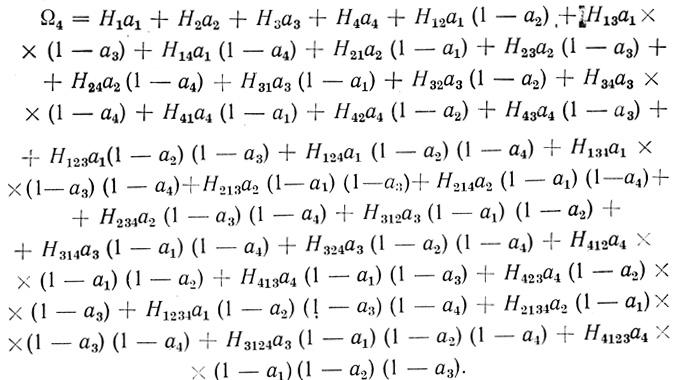 (3.30)
(3.30) Из (3.30) для каждой из (2n - 1) входных последовательностей (за исключением нулевой) получим по одному уравнению, в результате чего составляем систему из 15 уравнений:
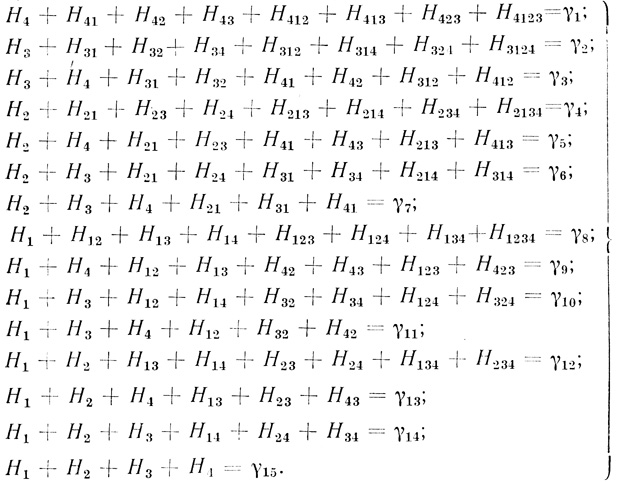 (3.31)
(3.31)Выберем l = 4⋅23 - 24 + 1 = 17 свободных переменных и обозначим их через набор хj:
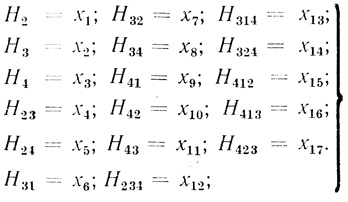 (3.32)
(3.32)Кроме этого, обозначим:
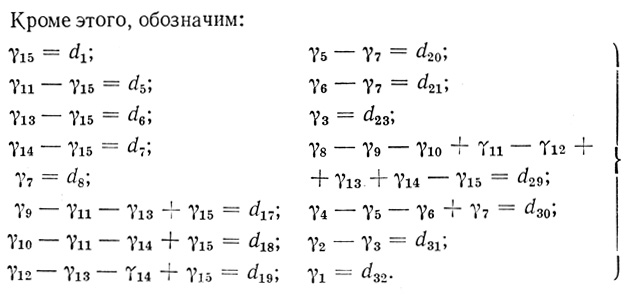 (3.33)
(3.33) Решив систему уравнений (3.31) относительно несвободных переменных с учетом (3.32) и (3.33), получим:
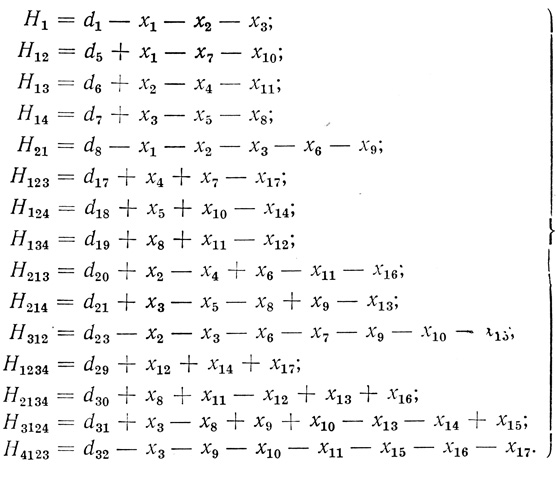 (3.34)
(3.34) Подставив (3.34) и (3.32) в (3.21), получим формулу для суммарного числа волокон четырех входового нейрона:
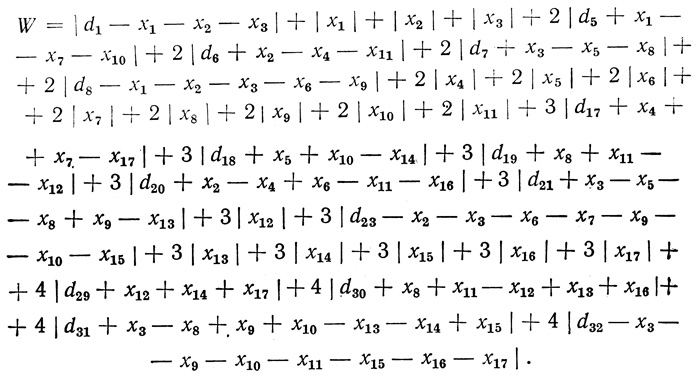 (3.35)
(3.35) 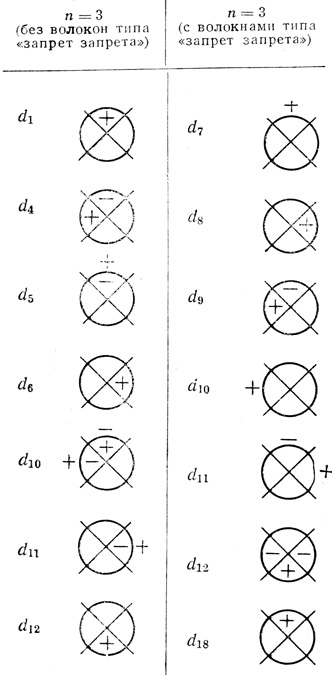
Таблица 3.1
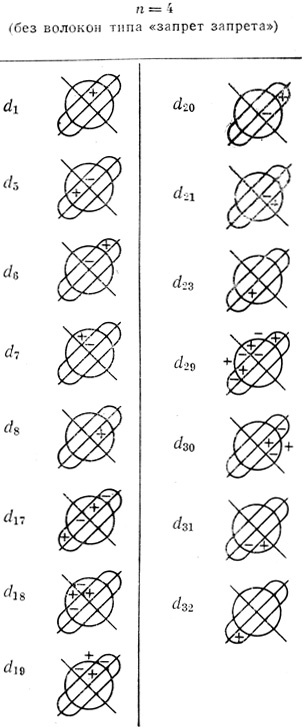
Таблица 3.2
Рассматривая формулы (3.25), (3.29) и (3.35), убеждаемся в том, что общая структура их символически может быть записана в следующем виде:
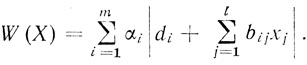
Здесь αi∈{1, 2, 3,....}; bij∈{ - 1; 0; +1}; di вычисляются по формулам (3.23), (3.27), (3.33) или определяются по вспомогательным табл. 3.1 и 3.2.
Для определения любой из величин di необходимо сложить γj отмеченные в диаграммах таблицы знаками плюс (+) и минус (-), причем γj, помеченные знаком плюс, берутся со своим знаком, а имеющие знак минус - с обратным. Используя вспомогательные таблицы, можно определить все величины di в уме, без необходимости производить вычисления по формулам (3.23), (3.27) и (3.33).
Теперь задача синтеза нейрона с минимальным числом волокон сводится к нахождению такого набора xj (j = 1,..., l), который, обеспечил бы получение наименьшего числа волокон Ŵ(хj) (j = 1,... l).
По выбранному набору x̂j (методы выбора излагаются ниже) и формулам типа (3.24), (3.28) и т. п. определяются все параметры Hi, по которым однозначно строится искомый формальный нейрон.
Б. Синтез нейрона с минимальным числом волокон методом линейного программирования
Для отыскания набора x̂j (j = 1,..., l), минимизирующего выражение для суммы волокон формального нейрона
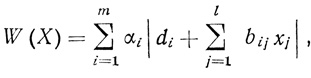 (3.36)
(3.36)принят симплексный метод линейного программирования.
Докажем, что минимизация выражения (3.36) эквивалентна следующей задаче линейного программирования: минимизировать линейную форму
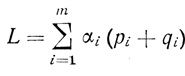 (3.37)
(3.37) при условиях
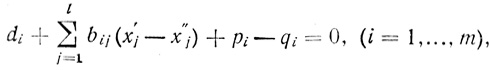 (3.38)
(3.38) где
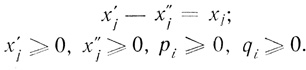 (3.39)
(3.39) Действительно:
1. Произвольное число xj можно представить в виде разности двух неотрицательных чисел: х'j и х"j (хj = х'j - x"j). При этом
а) если xj > 0, то можно положить х"j = 0 и тогда х'j = xj;
б) если xj < 0, то можно положить х'j = 0 и тогда - х"j = xj.
Аналогично выражение di + lj=1Σ bijxj которое для различных наборов xj может быть как положительным, так и отрицательным, представим в виде разности qi - рi неотрицательных переменных pi и qi, т. е.
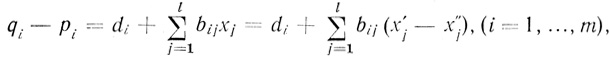 (3.40)
(3.40)что эквивалентно условиям (3.38).
При этом задача минимизации выражения (3.36). сводится к задаче минимизации выражения
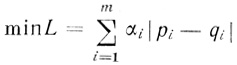 (3.41)
(3.41)при условиях (3.38), (3.39).
2. Заметим, что если вектор
X = (х'1,..., x'l, х"1,..., x"l, p ,..., рm, q1,...,qm) (3.42)
удовлетворяет условиям (3.38), (3.39) задачи, то этим же условиям удовлетворяет и вектор
Y = (х'1, ..., х'l, х"1,..., х"l, p'1..., р'm, q'1, ..., q'm), (3.43)
где
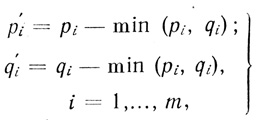 (3.44)
(3.44)так как pi - qi = p'i - q'i.
При этом
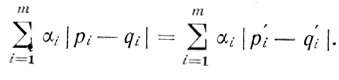 (3.45)
(3.45)Очевидно, что
p'iq'i = 0, i = 1,....., m; (3.46)
в силу (3.45) штрих при переменных рi и qi может быть опущен, и, следовательно, решение задачи (3.36), (3.38), (3.39) можно искать среди решений задачи
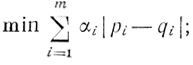 (3.47)
(3.47)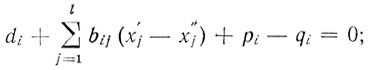 (3.48)
(3.48)piqi = 0; (3.49)
х'j ≥ 0, x"j ≥ 0, pi ≥ 0, qi ≥ 0. (3.50)
3. Из условий (3.49) и (3.50) следует, что
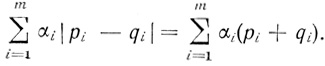 (3.51)
(3.51) Для того чтобы в этом убедиться, достаточно показать, что
|pi - qi| = (pi + qi), i = 1...., m;
а) из (3.49) следует, что при рi > 0 получим qi = 0 и, следовательно,
|pi - qi| = pi + qi;
б) при qi > 0 получим рi = 0 и, следовательно,
|pi - qi| = pi + qi;
в) при рi = 0 получим qi ≥ 0 и, следовательно,
|pi - qi| = pi + qi;
г) наконец, при qi = 0 получим pi ≥ 0 и, следовательно,
|pi - qi| = pi + qi;
Таким образом, при всех допустимых значениях рi и qi имеем
|pi - qi| = pi + qi;(3.52)
Таким образом, задача (3.47)-(3.50) эквивалентна задаче
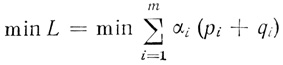 (3.53)
(3.53)при условиях (3.48)-(3.50).
4. Рассмотрим задачу (3.53), (3.48)-(3.50). Это - задача линейного программирования, и ее можно решать стандартной процедурой - симплексным методом.
Известно, что решение задачи линейного программирования находится среди векторов, Определяющих вершины многогранника условий задачи. Покажем, что если вектор (3.42) определяет вершину множества (3.48), (3.50), то
x'jx"j = 0 и piqi = 0,
т. е. если одна из координат пары x'jx"j (соответственно pi, qi) не равна нулю, то другая равна нулю.
Для этого запишем условия (3.38) в развернутой форме:
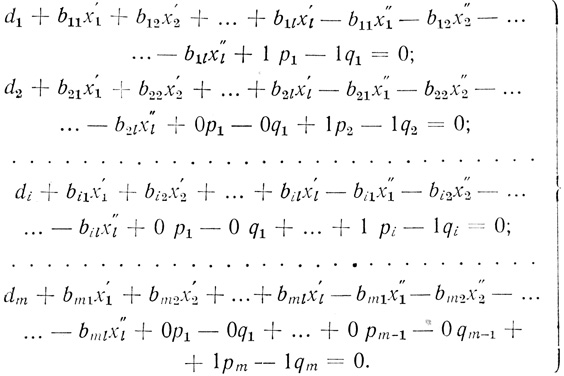 (3.54)
(3.54)Аналогично предложенному в [30] введем понятие векторов условий и вектора ограничений.
Под вектором условий В'j (соответственно B"j) понимают вектор, компонентами которого являются коэффициенты при х'j в условиях (3.38) (соответственно при х"j для B"j). Вектором ограничений D называется вектор, компонентами которого являются величины di в условиях (3.38).
Аналогично определим векторы условий Рi и Qi и запишем все векторы в виде
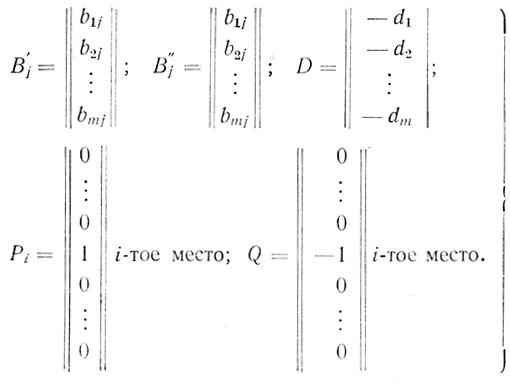 (3.55)
(3.55)Из (3.55) легко видеть, что B'j - B"j (j = 1,..., l), а Рi = - Qi, (i = 1,..., m).
Обозначим B'j = B"j = Вj. Тогда система ограничений (3.48) (или многогранное множество условий линейного программирования) может быть записана в векторной форме:
D + В1x'1 1 + В2x'2 + ... + Blx'l - B1x"1 - В2х"2 - ... - Blx"l + Р1p1 + Р2р2 + ...+ Рmрm - Q1q1 - Q2q2 - .... - Qmqm = 0. (3.56)
Воспользуемся теоремой 4 работы [30]: для того чтобы неотрицательные компоненты вектора
X (x'1,..., x'l, x"1,..., х"l , р1,..., рn, q1,......,qm),
удовлетворяющего условиям (3.48), определяли координаты вершины многогранника условий, необходимо и достаточно, чтобы система векторов B'j, B"j, Pi, Qi при ненулевых x'j, x"j, pi, qi была линейно независима.
Выше было отмечено, что B'j = В"j = Bj, а Рi = -Qi; отсюда вытекает, что если X - вершина, то при х'j ≠ 0, x"j = 0 и, наоборот, при x'j ≠ 0 x"j = 0, аналогично этому при pi ≠ 0 qi = 0, и, наоборот, при qi ≠ 0 рi = 0, в противном случае система векторов условий, отвечающая ненулевым координатам вершины X, была бы линейно зависима, что невозможно.
Итак, доказано, что если X - вершина, то
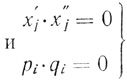 (3.57)
(3.57)Таким образом, показано, что если решать задачу (3.53), (3.48) (3.50) симплексным методом, то условие (3.49) будет автоматически выполняться и тем самым будет решена задача (3.53),(3.48) - (3.50).
5. В силу доказанного задача'минимизации числа волокон
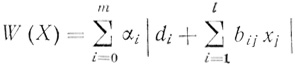 (3.58)
(3.58) эквивалентна задаче минимизации линейной формы
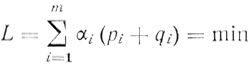 (3.59)
(3.59)при условиях
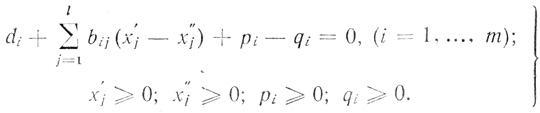 (3.60)
(3.60) Чтобы использовать стандартную программу решения этой задачи симплексным методом, введем единый символ для переменных и единую их индексацию:
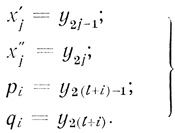 (3.61)
(3.61) Теперь задача сводится к минимизации линейной формы:
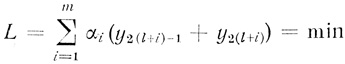 (3.62)
(3.62) при условиях:
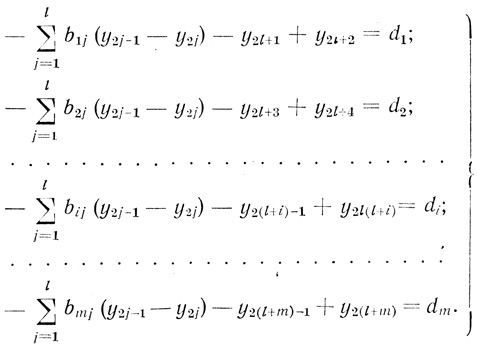
Общее количество переменных составляет величину
Кy = 2(l + m)= [(n - 1)2n + 1] 2.
Из этого числа первые 2l = n⋅2n - 2n+1 + 2 переменных необходимы для синтеза оптимального нейрона, а остальные 2m = n*2n переменных являются "паразитными" (но необходимыми для применения симплексного метода к минимизации суммы модулей).
В результате решения задачи минимизации линейной формы (3.62) при условиях (3.63) на ЭЦВМ получаем набор yi, который определяет искомые
x̂j = y2j-1 - y2j, (3.64)
Знак ∧ над хj - означает, что определенный таким образом набор xj обеспечивает минимальное количество волокон Ŵ. Поэтому найденные по x̂j величины Нi позволяют построить оптимальный в этом смысле нейрон.
Для удобства применения описанного метода приведем конкретный вид линейной формы (3.62) и условий (3.63) для наиболее часто встречающихся случаев синтеза нейрона с тремя и четырьмя входами:
Для n = 3 из (3.25) в соответствии с (3.61) - (3.63) находим линейную форму и условия: линейная форма
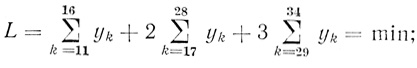 (3.65)
(3.65)условия
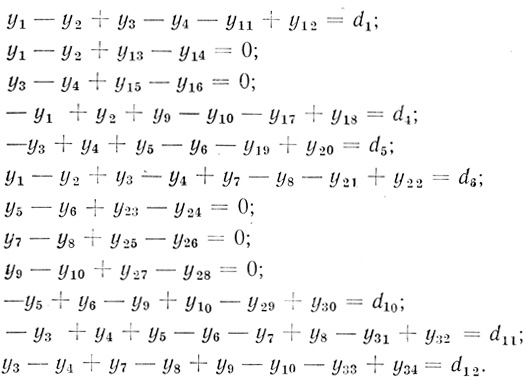 (3.66)
(3.66)Для n = 3 (с применением волокон типа "запрет запрета") из (3.29) в соответствии с (3.61) - (3.63) находим линейную форму и условия:
линейная форма
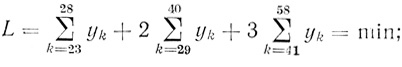 (3.67)
(3.67)условия
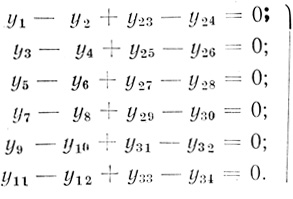
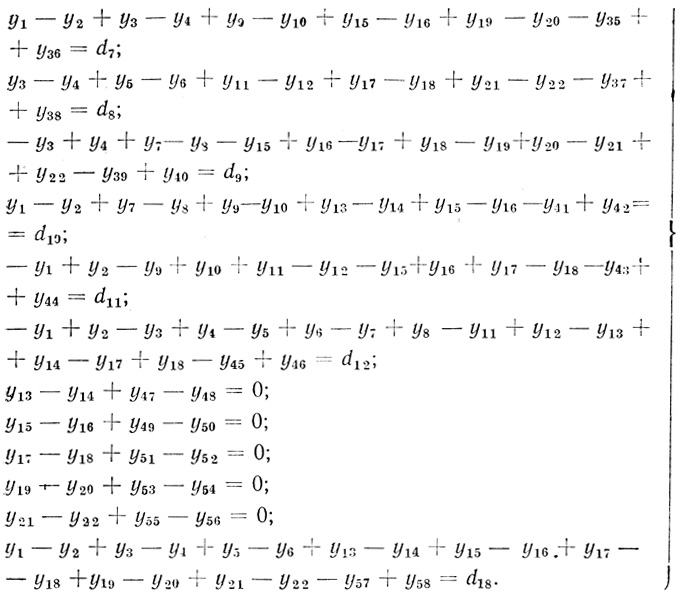 (3.68)
(3.68)Для n = 4 из (3.35) в соответствии с (3.61) - (3.63) находим линейную форму и условия: линейная форма
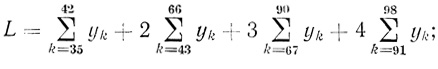 (3.69)
(3.69)условия
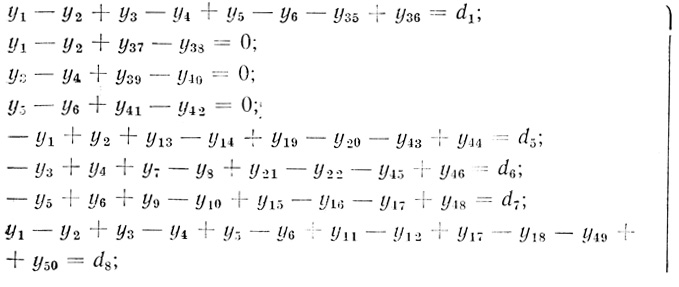
 (3.70)
(3.70)Для иллюстрации изложенной методики рассмотрим несколько примеров синтеза минимальных нейронов по их пороговым диаграммам.
Пример 1. Дана диаграмма Dθ = (0, 1, -2, 3, 1, -3, 2,4); необходимо синтезировать нейрон с наименьшим числом волокон.
По табл. 3.1 (или формулам (3.23)) определяем di: d1 = 4; d4 = 7, d5 = 2; d6 = 3; d10 = 6, d11 = - 5; d12 = 1.
Введя при этих данных условия (3.66) и линейную форму (3.65) в стандартную программу решения общей задачи линейного программирования и решив ее на ЭЦВМ, получаем
y1 = 2; y6 = 4; y7 = 1; остальные yi = 0.
Вычисляем по (3.64) x̂j.
x̂1 = Н̂2 = 2; х̂2 = Ĥ3 = 0; х̂3 = Н̂23 = - 4; x̂4 = Ĥ31 = 1;
x̂5 = Ĥ32 = 0.
Вычисляем по (3.24) Нi:
H1 = 2; H12 = 5; Н13 = 2; H21 = 0; H123 = 2; H213 = 0; H312 = 0.
Таким образом, получены все данные для синтеза минимального по числу волокон нейрона (рис. 3.4), реализующего заданную диаграмму.
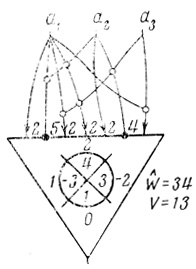
Рис. 3.4
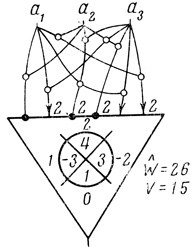
Рис. 3.5
Пример 2. Дана та же диаграмма, что и в первом примере; необходимо синтезировать нейрон с наименьшим числом волокон Ŵ и с использованием волокон типа "запрет запрета".
По табл. (3.1) (или формулам (3.27)) находим набор dγ:
d7 = 4; d8 = 3; d9 = 7; d10 = 1; d11 = 4; = 1; d12 = 4.
Введя при этих данных условия (3.68) и линейную форму (3.67) на перфокартах в ЭЦВМ, в результате решения получаем
y8 = - 1; y15 = 2; y21 = 2; остальные yi = 0.
По (3.64) с учетом (3.26) вычисляем:
x̂4 = H12 = - 1; х̂8 = Ĥ1(32) = 2; x̂11 = Н̂3(12) = 2; остальные xi = 0.
По (3.28) вычисляем:
Н̂23 = 0; Ĥ31 = 1; Н̂32 = -2; Ĥ123 = 0; Н̂213 = -2; Ĥ312 = 0; H3(21) = 0.
По найденным величинам Ĥi строим нейрон (рис. 3.5). Обратим здесь внимание на то, что нейрон имеет Ŵ = 26 волокон в то время как синтезированный по той же диаграмме нейрон в предыдущем примере имел Ŵ = 34 волокна. Введение волокон типа "запрет запрета" снижает общее количество волокон, потребных для реализации одной и той же логической функции.
Пример 3. Дана диаграмма Dθ = (0, 0, 0, 2, 1, -1, 1, 1, 0, 0, 1, 0, -1, 1, 1,2); необходимо построить нейрон с наименьшим числом волокон Ŵ.
По табл. (3.2) или формулам (3.33) определяем все di:
d1 = 2; d5 = -2; d6 = -1; d7 = -1; d8 = 1; d17 = 1; d18 = 2; d19 = 1, d20 = 2; d21 = 0; d23 = 2, d29 = 0, d30 = 2, d31 = 2, d32 = 0.
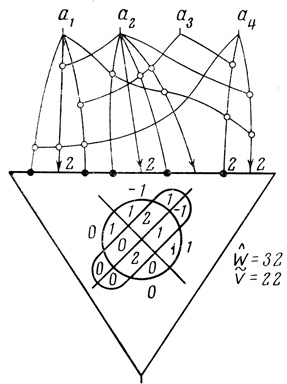
Рис. 3.6
С учетом найденных di в ЭЦВМ вводятся линейная форма (3.69) и условия (3.70). В результате решения задачи получено y3 = 1; y5 = 1; y20 = 2; y26 = 1; y29 = 2; y32 = 1; остальные yj = 0.
По (3.64) с учетом (3.32) находим:
x̂2 = Ĥ3 = 1; x̂3 = Ĥ4 = 1; x̂10 = Ĥ42 = -2; x̂13 = Ĥ314 = -1; x̂15 = Ĥ412 = 2; x̂16 = Ĥ413 = -1;
По (3.34) вычисляем:
Ĥ1 = 0; Ĥ12 = 0; Ĥ13 = 0; Ĥ14 = 0; Ĥ21 = -1; Ĥ123 = 1; Ĥ124 = 0; Ĥ134 = -1; Ĥ213 = 0; Ĥ214 = 2; Ĥ312 = 0; Ĥ1234 = 0; Ĥ2134 = 0; Ĥ3124 = 0; Ĥ4123 = 0; Ĥ14 = 0;
По найденным параметрам Ĥi строим минимальный нейрон (рис. 3.6) с числом волокон Ŵ = 32.
В. Целочисленность
Известно, что если у каждой вершины выпуклого многогранника в n-мерном пространстве все координаты целочисленны, то такой многогранник называется целочисленным. Применительно к условиям решения задачи линейного программирования, решаемой в настоящем параграфе, можно утверждать, что целочисленность многогранника условий не зависит от находящихся в правых частях равенств (3.66), (3.68), (3.70) величин di, которые, в свою очередь, по самой своей природе тоже целочисленны.
В работе [44] показано, что многогранник решений целочислен, если матрица A, составленная из коэффициентов при yi в условиях (3.63) обладает свойством унимодулярности. При этом говорят, что матрица обладает свойством унимодулярности, если каждый ее минор равен 0, + 1 или -1.
Составим матрицу А для случая, когда n = 3, и проверим, обладает ли она свойством унимодулярности. Из условий (3.66) следует, что матрица А имеет вид (3.71).
Матрица (3.71) имеет ряд очевидных особенностей, существенно облегчающих выявление ее унимодулярности:
а) все элементы матрицы равны 0, +1 или -1;
б) каждые два ненулевых элемента 2j - 1 и 2j (j = 1,...17) матрицы, находящиеся в любой строке, имеют противоположные знаки (в силу соотношения (3.64));
в) в каждой строке матрицы содержится четное число ненулевых элементов.
Произведя линейные преобразования над строками матрицы (3.71), легко свести ее к виду, который удовлетворяет необходимым и достаточным условиям унимодулярности теоремы Хеллера и Томпкинса [45]. Следовательно, многогранник решений при синтезе формальных нейронов с произвольной диаграммой Dθ (определяющей набор di) будет целочисленным. При синтезе нейронов с 4 условия "а" - "в" сохраняются, и поэтому есть все основания ожидать, что и для этих случаев свойство целочисленности сохранится.
Действительно, синтез нескольких сот нейронов по Dθ симплексным методом линейного программирования показал, что свойство целочисленности во всех случаях было сохранено.
Г. Многозначность решений
Симплексным методом линейного программирования по заданной пороговой диаграмме Dθ можно синтезировать не один формальный нейрон, а некоторое конечное множество нейронов, каждый из которых удовлетворяет Dθ и имеет минимальное число волокон W. Это утверждение вытекает из следующих соображений.
Можно доказать, что, для того чтобы точка Х0 (x01,...,x0l), являющаяся проекцией в пространство X (x1,...,xl) одной из вершин выпуклого многогранного множества
 (3.71)
(3.71)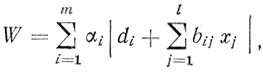 (3.72)
(3.72) была бы единственным минимумом выражения (3.72), необходимо и достаточно, чтобы она являлась минимумом выражения
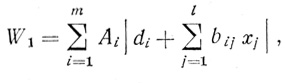 (3.73)
(3.73)где

a ε - произвольно малое положительное число.
Необходимость. Заметим, что точка Х0, являясь проекцией вершины многогранного множества, лежит на пересечении ряда гиперплоскостей
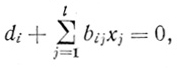
Поэтому в результате подстановки координат точки Х0 в уравнения этих гиперплоскостей они тождественно обращаются в нуль:

Допустим, что W1 (X) достигает минимума в точке Х1, отличной от Х0. Образуем разность
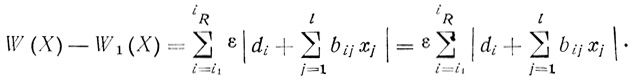 (3.74)
(3.74)Эта разность равна нулю в точке Х0 и положительна во всех остальных точках пространства X:
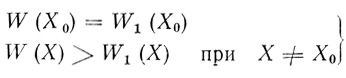 (3.75)
(3.75)В точке X1 в частности, получаем
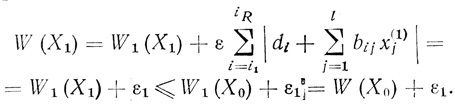
В силу произвольной малости s имеем W (Х1) ≤ W (Х0), что противоречит предположению о единственности минимума в точке X0.
Достаточность. Предположим, что функция W1 (X),
как и функция W (X), достигает минимума в точке Х0. Покажем тогда, что этот минимум для W (X) единственный.
Допустим противоположное: существует точка X1 такая, что
W (Х1) = W (Х0). (3.76)
Тогда в силу (3.75) и (3.76) [получим
W1 (X0) = W (Х0) = W (Х1) > W1 (Х1),
что невозможно, так как по предположению в точке Х0 функция W1 достигает минимума.
Из доказанного вытекает следующее простое правило проверки на многозначность решения задачи синтеза нейрона с минимальным числом волокон: а) в ЭЦВМ ввести di и получить набор x̂j; б) определить номера тех пар слагаемых в кусочно-линейной форме (3.62), которые при найденных значениях x̂j; обращаются в нуль; в) коэффициенты αi, находящиеся при найденных в пункте "б" слагаемых линейной формы (3.62), уменьшить на величину ε (во всех нижеприведенных примерах принято ε = 10-4); г) снова решить задачу линейного программирования при тех же di, но с измененной в соответствии с пунктом "в" линейной формой; если полученное решение совпадает с исходным решением, то минимальное значение Ŵ обеспечивается единственным набором значений x̂j по которому может быть построен один формальный нейрон с минимальным числом волокон Ŵ; если же при решении задачи с измененной линейной формой будет получен новый набор x̂(1)j обеспечивающий тот же минимум и, то может быть построен ряд формальных нейронов, имеющих одинаковое минимальное число волокон, обеспечивающих заданное функционирование. Для получения нейронов с различной конфигурацией волокон и одинаковым Ŵ необходимо в форме (3.62) смещать величину коэффициентов αi при нулевых слагаемых на величину е; комбинируя такие смещения по месту, занимаемому αi в линейной форме, и количеству слагаемых, в которых такое смещение производится, можно получить ряд различающихся между собой решений наборов x̂j.
Пример. На стр. 158 была задана пороговая диаграмма Dθ:
Dθ = (0, 0, 0, 2, 1,-1, 1, 1,0,0, 1,0, -1, 1, 1,2),
по которой с помощью методов линейного программирования нашли х̂1 = 1, x̂7 = -1, х̂15 = - 2, x̂16 = -2; остальные x̂j = 0; по этим данным был построен формальный нейрон (рис. 3.6) с Ŵ = 32.
При подстановке в формулу (3.69) найденных значений x̂j; оказалось, что слагаемые 3, 4, 5, 8, 9, 10, 11, 13, 14, 15, 16, 17, 20,22, 24, 25, 28, 29, 30, 32 обращаются в нуль. Поэтому в кусочно-линейной форме (3.69) все соответствующие этим номерам x̂j; уменьшаем на ε = 10-4 и снова решаем задачу на ЭЦВМ. В результате получаем новое решение: x̂2 = 1, x̂3 = 1, x̂10 = -2, x̂13 = -1, x̂15 = 2, x̂16 = -1, остальные x̂j = 0. Отличие нового решения x̂j(1) от основного x̂(2)j говорит о том, что W (xj) достигает минимума более чем в одной точке. Осуществив поиск новых решений в соответствии с изложенными правилами, удалось найти одно за другим еще 13 решений, которые сведены в табл. 3.3*.
* (При этом задача исчерпания всех возможных решений не ставилась.)
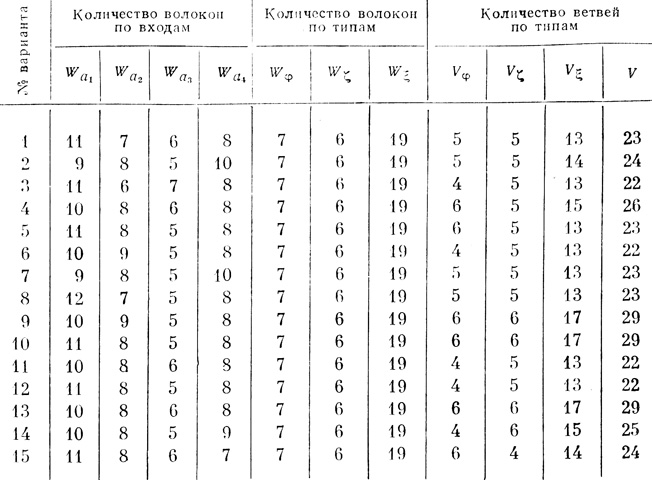
Таблица 3.3
Анализ табл. 3.3 (подтвержденный анализом нескольких сот решений аналогичных примеров, не вошедших в настоящую работу) позволяет сделать следующие выводы.
1. Общее число волокон W распределяется между входами a1,... ...,аn для различных вариантов решения задачи по-разному и неравномерно.
2. Количество волокон по типам (возбуждающие, тормозящие, запрещающие) остается неизменным для всех вариантов решения задачи (в данном примере для всех вариантов решения нейроны имеют по 7 возбуждающих, 6 тормозящих и 19 запрещающих волокон).
3. Количество ветвей V (как суммарное, так и по типам) для различных вариантов решения различно, причем наименьшему суммарному числу ветвей V соответствует наименьшее число запрещающих ветвей Vξ.
Из сказанного вытекает рекомендация: при синтезе формального нейрона с минимальным числом волокон Ŵ необходимо прежде всего проверить решение на многозначность. При наличии нескольких решений выбрать то из них, которое содержит относительно других наименьшее число ветвей Ṽ. В данном примере такие решения дают варианты 3, 6, 11 и 12.
На рис. 3.7 показан нейрон, построенный по варианту 6:
х1 = Н2 = 2, x4 = Н23 = - 1, x5 = H412 = - 2, х16 = H413 = -2;
из (3.34):
H14 = -1, H21 = -1, H124 = 2, H134 = -1, H213 = 1,
остальные параметры равны нулю. Построенный нейрон имеет минимальное число волокон Ŵ = 32 и относительно наименьшее число ветвей V̂ = 22.
Не исключена возможность того, что построенный нейрон является оптимальным, т. е. содержит минимальное число как волокон Ŵ, так и ветвей V̂. Однако для последнего утверждения необходима специальная проверка, связанная с синтезом нейрона по минимальному числу ветвей и многозначностью решения этой задачи (см. § 3.6). Сопоставляя некоторые совокупности минимальных решений по Ŵ и V̂, можно выбрать пересекающиеся совокупности наборов x̂̂j которые определяют структуру нейронов одновременно минимальных как по числу волокон Ŵ̂, так и по числу ветвей V̂̂, т. е. оптимальных нейронов.
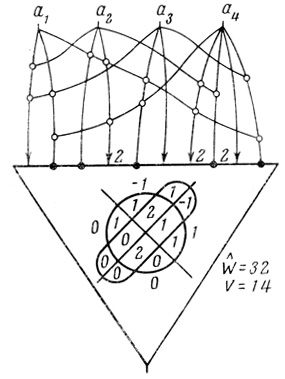
Рис. 3.7
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'