§ 3.5. Синтез формальных нейронов с минимальным числом волокон на аналоговых ЭВМ

Синтез минимальных по числу волокон нейронов, основанный на поиске значений свободных переменных x̂_j (j = 1,..., l), обеспечивающих минимальное значение Ŵ суммы всех волокон W, осуществлен также при помощи автоматической оптимизации на моделирующей установке ЭМУ-10.

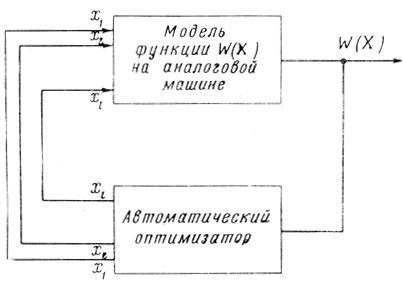
Рис. 3.8

Моделирующая установка совместно с автоматическим оптимизатором (рис. 3.8) обеспечивают минимум функции W = W (х₁,... ..., x_j,..., x_l), где l = n*2^n-1 - 2n + 1, причем функция W и искомые значения x̂_j, минимизирующие эту функцию, заранее не известны.

Оптимизатор автоматически подбирает величины х₁,..., x_l так, чтобы был достигнут минимум Ŵ функции W (X). Движение к минимуму происходит путем подсчета последовательно по всем переменным x_j рабочих приращений, пропорциональных частным производным соответствующих переменных. По частным производным, полученным по всем переменным, находится вектор градиента

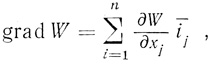(3.77)

где i^-_j - орты в пространстве х₁,..., x_j,..., x_l (х_i предполагаются декартовыми координатами). После определения градиента в данной точке делается шаг по направлению, противоположному направлению градиента, а затем в новой точке снова определяется градиент, делается следующий шаг и так далее. Таким образом, достигается наискорейшее уменьшение величины W (X), вплоть до получения Ŵ (X̂).

Общая идея автоматической оптимизации была изложена в работе [31].

На рис. 3.9 показана принципиальная блок-схема автоматической минимизации W при помощи универсальной моделирующей установки ЭМУ-10 и автоматического оптимизатора^*.

^* (Схема разработана инженером Ю. А. Бортнюком.)

Синтез формальных нейронов с минимальным числом волокон производился для случая, когда n = 3 по ранее выведенной формуле:

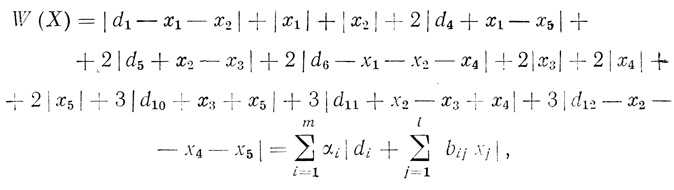(3.78)

где m = n*2^n-1; l = n*2^n-1 - 2ⁿ + 1.

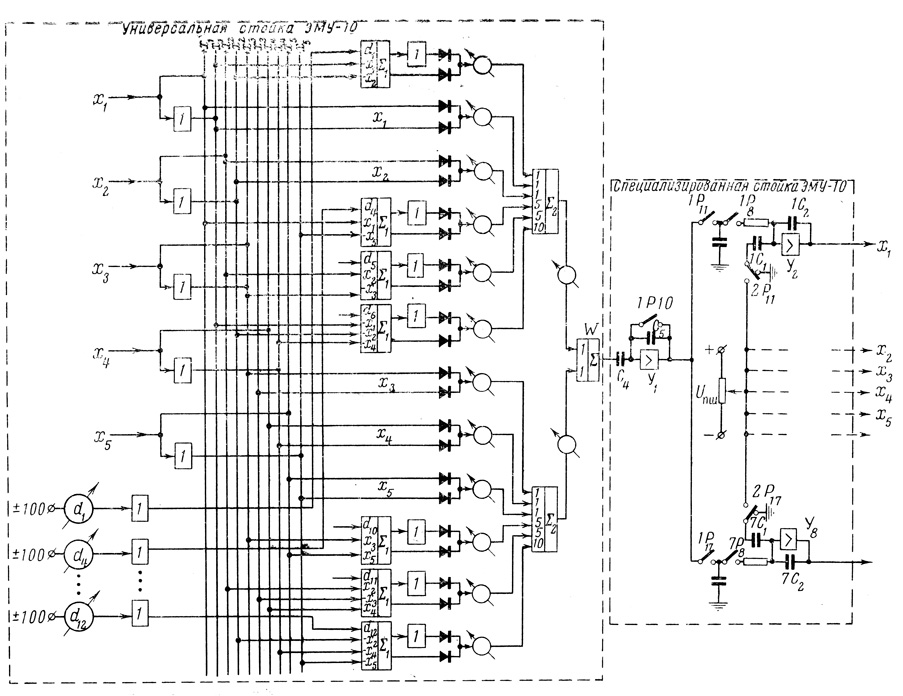
Рис. 3.9

Текущие (а в начале работы - произвольно установленные) значения x_j из интеграторов (y₂,......,y₆) оптимизатора непосредственно поступают на универсальную стойку моделирующей установки, где отрабатывается модель по зависимости (3.78). Преобразователи (1) обращают те из x_j, которые должны в соответствии с (3.78) иметь обратный знак.

Постоянные коэффициенты d_i для каждой конкретной диаграммы, заданной для реализации в виде нейрона с минимальным числом волокон, набираются на потенциометрах. Коэффициенты d_i и переменные величины х_j и - х_i подаются на усилители для получения алгебраических сумм ∑₁ слагаемых формулы (3.78). После этого диодные схемы выделяют модули полученных на усилителях Σ₁ сумм вида

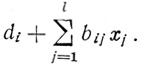
Величины а_i представляются в виде масштабных коэффициентов.

Полученные модули суммируются затем усилителями Σ₂ и Σ₃, в результате чего на выходе последнего усилителя получается текущее значение функции W (X). Функция W (X), полученная на модели в виде напряжения, подается на стойку автоматического оптимизатора.

Автоматический оптимизатор представляет собой самонастраивающуюся систему, обеспечивающую автоматический поиск условий, при которых функция W нескольких переменных х_j может иметь минимум. Движение к экстремальной точке происходит путем подачи одновременно по всем переменным рабочих приращений, пропорциональных частным производным соответствующих переменных. Работа оптимизатора происходит циклами. В каждом цикле проводятся пробные шаги, которые состоят в последовательной даче приращений Δх_j по каждой из переменных отдельно и в определении составляющих dW/dx,- градиента grad W в некоторой начальной точке М₀. В конце каждого цикла (т. е. после последовательного определения всех dW/dx_j) производится рабочий шаг, который происходит по направлению, противоположному направлению градиента. При этом переменные х_j получают дискретное приращение

где k = const > 0.

В новой точке (обозначим ее через М₁) для всех x_j производится новый цикл пробных шагов, снова определяется градиент, после чего производится новый рабочий шаг по направлению, противоположному направлению вновь найденного градиента, и т. д.

Так продолжается до тех пор,, пока величина

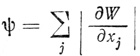
окажется меньше некоторой заранее заданной малой постоянной ψ₁. При этом величина W достигает минимального значения Ŵ, а поступающие с интеграторов (y₁,.....,y₈) оптимизатора величины х_j являются в этом случае оптимальными значениями x̂_j, по которым может быть построен формальный нейрон с минимальным числом волокон (см. § 3.4).

Длительность каждого шага определяется величиной k из (3.79); при малом значении k осуществляется точный поиск минимума, при больших значениях k - грубый. Вначале осуществляется грубый поиск, который позволяет приближенно отыскать место минимума, а затем система переводится на малый шаг и место минимума находится более точно. Рассмотрим несколько подробнее работу схемы рис. 3.9. Начальное значение переменных выставляется на усилителях y₂,......,y₆ оптимизатора произвольным образом. В том случае, когда на вход усилителей не подается напряжение, на их выходах сохраняется то напряжение, которое имело место в момент отключения входов.

Определение частных производных осуществляется следующим образом. При значениях x_j0, представляемых в оптимизаторе напряжениями, производится запоминание экстремизируемой функции W₀. ДЛЯ этого замыкается контакт 1 Р₁₀ и на выходе усилителя y₁ устанавливается напряжение, равное нулю. Конденсатор С₄ заряжается до напряжения uw, соответствующего значению функции W в точке (х₁₀, x₂₀,...,x_l0). Затем контакт 1 Р₁₀ размыкается и срабатывает реле Р₁₁. Это реле своим контактом 2 Р₁₁ изменяет напряжение на конденсаторе 1 С₁ на величину U_пш (напряжение пробного шага). При этом на выходе усилителя y₂ происходит изменение напряжения на величину

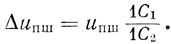
Напряжение на выходе усилителя y₂ представляет переменную х₁, следовательно, в момент срабатывания реле Р₁₁ подается пробное приращение Δu_пш по первой переменной. При поступлении на конденсатор С₄ нового значения напряжения, соответствующего функции W (х₁₀ + Δu_пш, x₂₀,..., х_l0), на выходе усилителя y₁ выделяется разность

В оптимизаторе принято отношение С₄/С₅ = k = 10, т. е. происходит усиление приращения функции в 10 раз.

Конденсатор 1 С₃ через контакт 1 Р₁₁ подключается к выходу усилителя ух и заряжается до напряжения Δu₁. Ввиду постоянства и небольшой величины Δu_пш напряжение Δu_пш = dW/dx₁. Аналогично происходит операция определения частных производных по другим переменным x_j.

После того как все запоминающие конденсаторы заряжены до напряжения

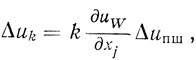
производится рабочий шаг, который делается по направлению, противоположному направлению градиента. Для этого входы интеграторов y₁,..., y_l через контакты 1 Р₈, ..., l Р₈ присоединяются к соответствующим конденсаторам, и на выходе интеграторов получается приращение напряжения

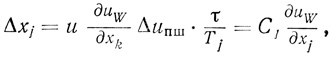
где τ - длительность рабочего шага, a T_j - постоянная времени интеграторов. Напряжение на запоминающем конденсаторе во время рабочего шага уменьшается, однако это изменение мало, так как постоянная времени разряда в 10 раз больше постоянной времени интеграторов.

Получив дискретные приращения Δx_j, переменные х_j перемещают значения функции W из начальной точки М₀ в новую точку М₁ (на рис. 3.10 показан случай двух переменных: х₁ и х₂). В но вой точке производится следующий цикл, т. е. запоминается изменившееся значение функции W, определяются ее частные производные и осуществляется рабочий шаг по направлению, противоположному направлению градиента. Циклы повторяются, как уже отмечалось, до тех пор, пока величина φ = _jΣ|dW/dx_j| окажется меньше некоторой достаточно малой постоянной ψ₁ причем W достигает минимального значения Ŵ, а обеспечивающие его х̂_j считываются в качестве искомых.

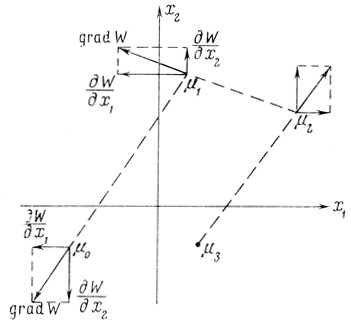
Рис. 3.10

Точность поиска экстремума значения функции W может регулироваться величиной τ, а также величиной пробного шага Δu_пш. В зависимости от них можно осуществлять грубый и точный поиск значения экстремума функции W (X).

Автоматический оптимизатор может работать как по методу градиента, так и по методу быстрого спуска. При этом если приращение функции W (X) имеет нужный знак и превосходит некоторое заданное значение ΔW_H то рабочий шаг по прежнему градиенту повторяется. Если ΔW < ΔW_H, то происходит определение нового градиента. Таким образом, метод быстрого спуска используется вдали от экстремума, когда производные велики, а затем происходит переход на метод градиента, т. е. определение градиента после каждого рабочего шага, вблизи от экстремума, где производные функции малы.

После проверки значения приращения функции происходит запоминание нового значения функции, для чего замыкается контакт 1 Р₁₀ и происходит или повторение рабочего шага, или определение нового градиента.

В оптимизаторе также предусмотрено введение ограничений, накладываемых на координаты исследуемого объекта. Время решения одной задачи в зависимости от масштаба пробных шагов и характера поведения функции W (X) колеблется от 5 до 20 мин.

Величины х̂_j считываются с цифрового оптического индикатора с достаточно большой точностью (до десятых долей вольта). При решении одной и той же задачи (т. е. при фиксированном наборе d_i), но с различными начальными значениями х̂_j⁽⁰⁾ можно получить несколько различных наборов х̂_j⁽¹⁾,...,х̂_j^(k) обеспечивающих минимальное число волокон Ŵ. Факт многозначности решения задачи синтеза нейронов с минимальным числом волокон впервые был обнаружен при работе с моделирующей установкой и автоматическим оптимизатором по изложенной методике.

Помимо синтеза обычного трехвходового формального нейрона, на установке был также осуществлен синтез трехвходовых нейронов с использованием волокон типа "запрет запрета". Для этого на универсальной стойке была набрана модель, соответствующая формуле (3.29), которая содержит 11 переменных. В связи с этим пришлось использовать две стойки автоматических оптимизаторов (так как одна стойка обеспечивает оптимизацию по 7 переменным). Для синтеза четырехвходовых нейронов пришлось бы использовать уже три оптимизатора. Рост необходимого оборудования с увеличением n и сравнительно большое машинное время, потребное для решения одной задачи, являются главными недостатками описанного метода. Вместе с тем он дает вполне удовлетворительные результаты и при невозможности использования ЭЦВМ может быть применен для синтеза формальных нейронов с минимальным числом волокон Ŵ. Результаты, полученные методом автоматической оптимизации на моделирующей установке, совпали с результатами решения тех же задач методом линейного программирования на ЭЦВМ.