§ 3.6. Синтез формальных нейронов с минимальным числом ветвей на ЭЦВМ

При некоторых вариантах технической реализации формальных нейронов физически воссоздаются ветви, а не отдельные волокна. Вес ветви, т. е. количество волокон, которое в нее входит, определяется при этом лишь параметрами ветви (в частности, величиной ее сопротивления). Напомним, что ветвью называется пучок волокон, изображаемый (а в отдельных, здесь упоминаемых, случаях и реализуемый) в виде одного волокна с весом-числом, указывающим эквивалентное количество волокон в этом пучке. Вполне понятно, что в случаях, когда физически воссоздаются не волокна, а ветви, практически более интересной становится задача синтеза нейронов с минимальным числом ветвей V̂, нежели задача синтеза нейронов с минимальным числом волокон Ŵ, решенная в предыдущих двух параграфах.

Для решения задачи синтеза нейрона с минимальным числом ветвей V̂ прежде всего необходимо определить общее количество ветвей V. Воспользуемся для этого тем же подходом, который был применен ранее для нахождения общего числа волокон W (§ 3.4,А).

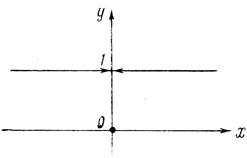
Рис. 3.11

Величины H_i (i ∈ {i, ij, ijk,...}) в формулах (3.19), (3.20) и (3.21) в соответствии с их местом в аналитическом выражении n переменных определяют число волокон того или иного типа. Однако сам факт неравенства нулю любой из этих величин означает наличие одной ветви данного типа. Например, если H₂= -3, то это значит, что имеется одна тормозящая ветвь, принадлежащая второму входу (то, что эта ветвь имеет вес 3, нас при подсчете числа ветвей не интересует); если же H₂₁ = -3, то это значит, что от второго входа идет одна тормозящая ветвь, но так как эта ветвь запрещается одной ветвью первого входа, то здесь окажется уже две ветви, что при подсчете общего числа ветвей необходимо учесть. Таким образом, для подсчета общего числа ветвей необходимо руководствоваться следующими правилами: в аналитическом выражении для данного числа переменных n:

1) выявить все величины Н_i, не равные нулю;

2) вместо каждой из величин Н_i, не равных нулю, поставить единицу, умноженную на коэффициент, равный числу индексов при Н_i)

3) полученные величины просуммировать.

Чтобы выразить это правило формулой, необходимо подобрать функцию (рис. 3.11), которая удовлетворяет условию

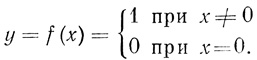
Очевидно, что такой функцией является функция y = sign² х. Также очевидно и то, что параметры Н_i зависят только от числа переменных n и логики диаграммы (т. е. от величин 47); это позволяет для фиксированных n и γ_j воспользоваться формулами для общего числа волокон W и всей принятой при этом формализацией, заменив лишь модули параметров Н_i на функции вида sign² Н_i. Тогда общее число ветвей для n = 3 в соответствии с (3.25) выразится формулой

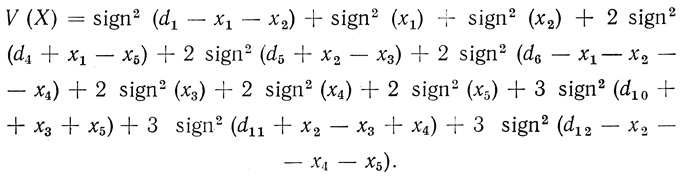(3.80)

Формализация величин x_j соответствует (3.22); d_i вычисляются по формулам (3.23) или определяются по табл. 3.1; Н_i вычисляются по формулам (3.24).

В случае, если при n = 3 используются волокна типа "запрет запрета", число ветвей с учетом (3.29) будет

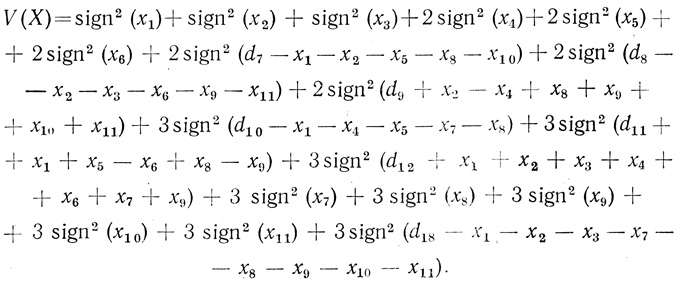(3.81)

Величины x_j, d_i, Н_i соответствуют (3.26) - (3.28).

Наконец, при n = 4 суммарное число ветвей в соответствии с (3.35) найдем по формуле

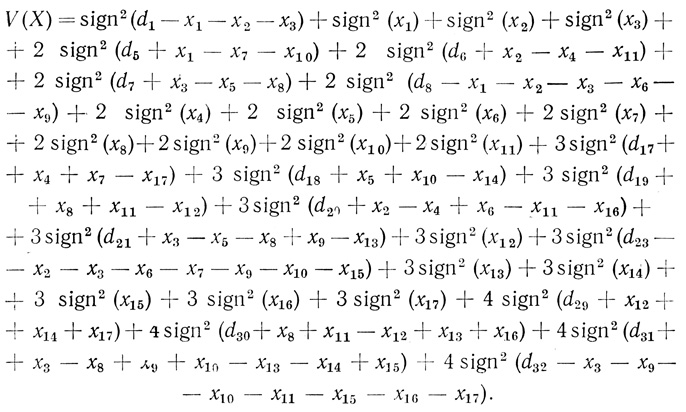(3.82)

Формализация в (3.82) та же, что и в (3.32); параметры d_j вычисляются по (3.33) или определяются по табл. 3.2; величины Н_i вычисляются по формулам (3.34).

Формулы (3.80) - (3.82) можно объединить в одной символической записи для любого n:

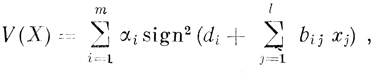(3.83)

где α_i ∈ {1, 2, 3,...}; b_ij ∈ { - 1; 0; + 1}; d_i = d_i (γ_j) вычисляются по формулам (3.23), (3.27), (3.33) или определяются по вспомогательным табл. 3.1 и 3.2; при отсутствии волокон типа "запрет запрета"

Теперь задача синтеза формального нейрона с минимальным числом ветвей V̂ сводится к нахождению такого набора x̂_j (j = 1, ..., l), который обеспечил бы минимизацию выражения (3.83). Знание X̂ необходимо и достаточно для того, чтобы определить значения всех переменных Н_i аналитического выражения Ω_n и, следовательно, чтобы построить нейрон с минимальным числом ветвей.

Задачу нахождения набора X̂, обеспечивающего минимизацию выражения (3.83), ни одним из известных методов математического программирования решить не удалось. Поэтому пришлось прибегнуть к разумно организованному автоматическому перебору на ЭЦВМ. Решение задачи при этом сводится к следующему:

1) в ЭЦВМ вводятся запрограммированная формула (3.83) и набор значений d_i, необходимых для синтеза конкретного нейрона;

2) специальный блок автоматически формирует наборы из I чисел каждый, которые используются в качестве X для вычисления величин V (X) по формуле (3.83) при заданных d_i;

3) каждое очередное значение V⁽ⁱ⁾ (X) сравнивается с предыдущим (X) и записывается в памяти вместо него только при условии, если

4) вычисления по пунктам 2 и 3 идут до полного исчерпания всех наборов X, какие только могут быть организованы из некоторой заданной матрицы, состоящей из с строк и l столбцов (вид матрицы и организация перебора будут описаны ниже); в результате выполнения процедуры по пункту 3 при правильно организованной матрице, из которой формируются наборы X, после окончания перебора в памяти машины оказывается записанным минимальное значение числа ветвей V̂ и соответствующий ему набор значений X, которые и выдаются на печать;

5) введя в машину найденное значение V̂, можно выдать на печать все различные варианты Х₁,..., X_s, которые обеспечивают синтез нейронов с минимумом ветвей V̂.

Имея s наборов X, можно вычислить по обычным правилам все Н̂_i и построить s различных нейронов, удовлетворяющих заданной логике при минимальном числе ветвей V̂. Это дает возможность из s нейронов, равноценных по количеству ветвей, выбрать один по каким-то дополнительным критериям, например по относительному W̃ или абсолютному Ŵ минимуму волокон.

Рассмотрим организацию перебора и построение матрицы, из которой он осуществляется.

Пусть задана матрица из с строк и l столбцов вида

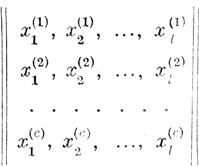(3.84)

из которой должны быть составлены все возможные, различающиеся между собой, последовательности х⁽ⁱ⁾₁, x^(j)₂,......,x^(k)_l из l элементов

каждая, где i, j_j,....., k ∈ {1, 2,...., с}. Например, из матрицы с l = 2, с = 3 вида

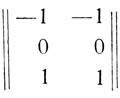
может быть составлено следующих 9 различающихся между собой последовательностей:

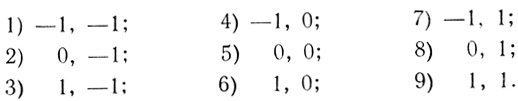
Вообще матрица из с строк и l столбцов позволяет образовать z = с^l различающихся между собой последовательностей по l элементов каждая.

Необходимо так организовать построение z последовательностей, чтобы можно было составить циклически работающую программу для ЭЦВМ. При этом в каждом из l циклов должно производиться с повторений.

Этим требованиям вполне удовлетворяет такой алгоритм организации перебора: строится таблица из l столбцов, причем

а) в первом столбце с^l-1 раз последовательно записываются с элементов первого столбца матрицы, так что всего в первом столбце оказывается с^l элементов;

б) во втором столбце таблицы каждым с строкам первого столбца соответствует одна строка, т. е. всего с^l-1 строк, в которых с^l-2 раз последовательно повторена запись с элементов второго столбца исходной матрицы и т. д.;

в) в последнем l-том столбце имеется с строк, в которых размещается с элементов исходной матрицы;

г) для получения всех z возможных различающихся между собой последовательностей из l элементов каждая достаточно из построенной в соответствии с пунктами "а" - "в" таблицы выписать элементы каждой из с^l строк. Например, пусть исходная матрица имеет вид

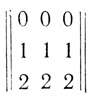
Построим для нее таблицу (табл. 3.4) согласно пунктам "а" - "в" и рядом выпишем все z = с^l искомых наборов:

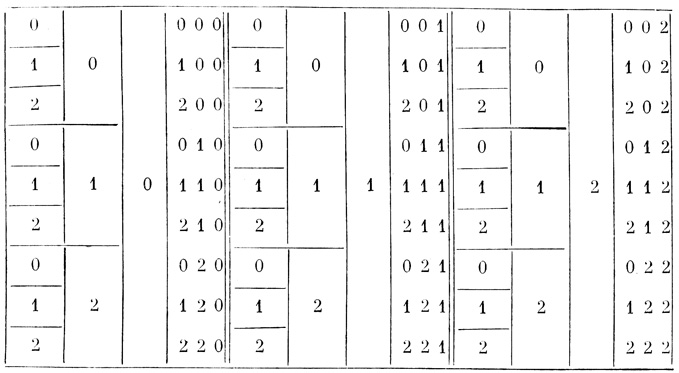
Таблица 3.4

Легко видеть, что такая организация перебора позволяет задать машине лишь минимальную информацию: первый элемент первой строки, закон построения последующих элементов первого столбца, число строк с и число столбцов l. При этом ЭЦВМ получает возможность автоматически производить циклический полный перебор для любого произвольно заданного количества столбцов и строк, причем производится l циклов по с повторений в каждом.

Теперь нужно выбрать исходную матрицу из l столбцов и некоторого числа с строк, из которых должны формироваться наборы x_j.

Опыт решения нескольких сот задач по синтезу нейронов с минимальным числом волокон Ŵ с использованием метода линейного программирования показал, что величины x̂_j по абсолютной величине не превосходят нескольких единиц. Исходя из этого, было решено для случая n = 3 (l = 5) исследовать решения задачи при с₁ = 5, с₂ = 7, с₃ = 9 и с₄ = 11 строках.

Для того чтобы матрицы можно было формировать как симметричные относительно нуля, так и несимметричные, в качестве исходной информации выбраны первый элемент первой строки x₁⁽¹⁾ и число строк с.

Приведем несколько примеров таких матриц при различных исходных данных:

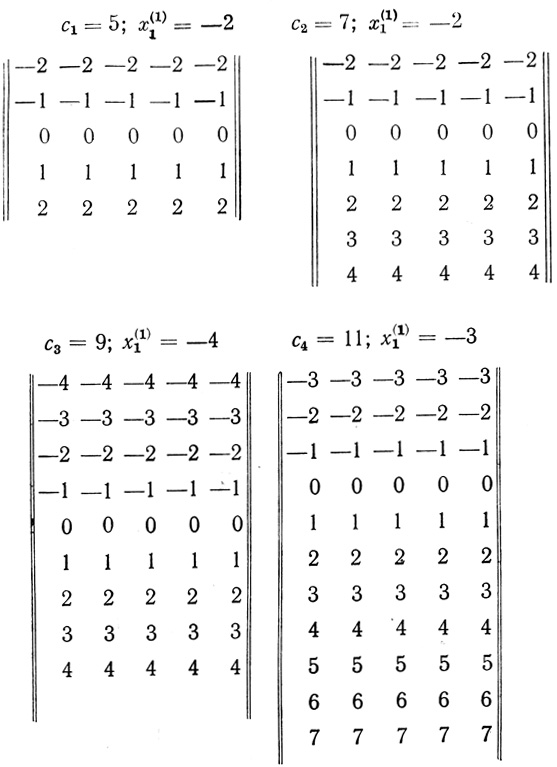
При построении матриц, симметричных относительно нуля, элементы первого столбца формируются по зависимостям:

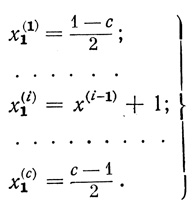(3.85)

Вообще для произвольного х⁽¹⁾₁ имеем:

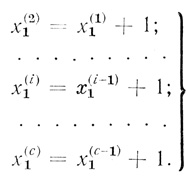(3.86)

Матрицы для любых других n формируются аналогично, но с учетом изменения числа столбцов l.

Для,того чтобы проверить эффективность рассматриваемого метода, при его помощи было решено большое число задач на синтез нейронов с минимальным числом волокон Ŵ по формуле (3.25). При этом выбирались только те задачи, которые предварительно были решены методом линейного программирования.

Так, пример 1, решенный на стр. 156 методом линейного программирования, был решен методом автоматического перебора. Задача решалась при 5, 7, 9 и 11 строках исходной симметричной относительного нуля матрицы, в результате чего было получено 129 различных нейронов, каждый из которых удовлетворял заданной пороговой диаграмме D^θ и имел минимальное число волокон Ŵ = 34, что совпадает с решением этой задачи методом линейного программирования.

Зависимость количества решений от числа строк, количество перебранных вариантов и расход машинного времени ЭЦВММ-20 показаны в табл. 3.5.

Таблица 3.5

Анализ полученных решений позволил сделать следующие выводы.

1. Все выданные на печать наборы X̂ обеспечивают построение нейронов с минимальным числом волокон Ŵ, что подтверждено параллельными решениями тех же задач методом линейного программирования.

2. Общее количество решений растет с увеличением числа строк, но все решения, полученные при числе строк, меньшем данного c, входят в последнее. Таким образом, все решения, полученные при 5, 7, 9 строках, входят в те 129 решений, которые были получены при с = 11. При увеличении числа n (и, следовательно, количества столбцов исходной матрицы) машинное время существенно возрастает.

Учитывая полное совпадение результатов решения задачи синтеза нейронов с минимальным числом волокон методом автоматического перебора с результатами решения той же задачи методом линейного программирования, считаем возможным применить первый из методов для синтеза нейронов с минимальным числом ветвей V̂ в соответствии с формулой (3.83).

В качестве примера рассмотрим синтез нейрона с минимальным числом ветвей V̂, по диаграмме которого ранее решалась задача на W:

Будем решать задачу, когда исходный элемент для построения матрицы (3.84) принимает значения x⁽¹⁾₁ = (1- с)/2. Столбец формируется по правилу: x⁽ⁱ⁾₁ = x^(i-1)₁ + 1. Расчет производится для случая, когда число строк с равно 5, 7, 9, 11. На печать выдаются наборы x̂_j, обеспечивающие минимальное значение числа ветвей по формуле (3.83) и само значение V̂. Результаты решения сведем в табл. 3.6. Кроме того, для всех найденных наборов х̂_j, обеспечивающих V̂, вычислим по формуле (3.25) значения W, которые также занесем в таблицу.

Анализ полученных результатов позволяет сделать следующие выводы.

1. Все 10 не повторяющихся наборов X̂. содержатся в решениях, полученных при с = 11; поэтому при необходимости иметь некоторое множество решений следует выбрать величину с по возможности большей.

2. Весьма замечателен и важен для практики тот факт, что среди десяти не повторяющихся наборов X̂, обеспечивающих синтез нейрона с минимальным числом ветвей V̂, имеется три набора X̂, которые одновременно обеспечивают синтез нейрона как с минимумом ветвей V̂, так и с минимумом волокон Ŵ, т. е. синтез оптимальных нейронов. При с = 11 такие решения дают варианты 15, 18 и 20. Для этих вариантов Ŵ = 34, а синтез этого же нейрона методами линейного программирования (см. стр. 156, пример 1) и автоматического перебора (см. стр. 178) показал, что данное число волокон является для него наименьшим. Таким образом, одновременная минимальность ветвей (V̂ = 12) и волокон (Ŵ = 34) позволяет считать варианты 15, 18 и 20 оптимальными, а обеспечивающие их значения X будем обозначать через X̂̂. По формулам (3.24) для этих вариантов вычислим остальные H_i и сведем результаты в табл. 3.7.

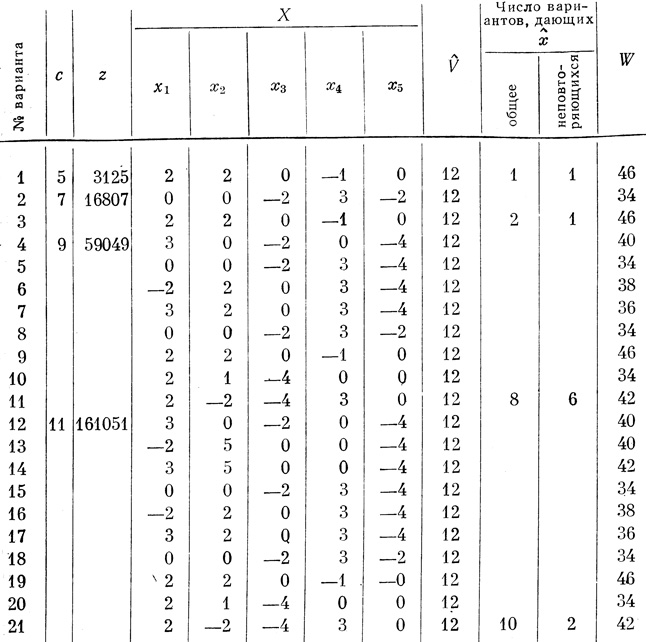
Таблица 3.6

По данным этой таблицы построим формальные нейроны (рис. 3.12), некоторые основные данные которых сведем в табл. 3.8.

Анализ табл. 3.8 показывает еще один замечательный эмпирический результат: если все нейроны с минимальным числом Ŵ по числу запрещающих волокон равноценны, то среди оптимальных нейронов могут оказаться такие, которые имеют относительно меньшее количество запрещающих ветвей (например, в варианте 20 имеется 5 запрещающих ветвей, в то время как в вариантах 15 и 18 - по 6).

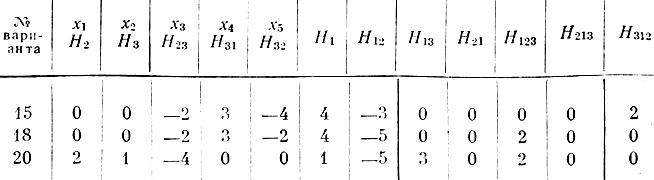
Таблица 3.7

Таблица 3.8

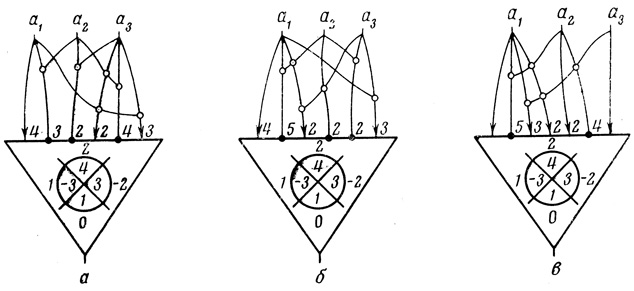
Рис. 3.12

Отсюда следует сделать вывод о целесообразности построения по заданной пороговой диаграмме всех оптимальных нейронов с тем, чтобы выбрать из них тот, который имеет относительно меньшее число запрещающих ветвей. Для того чтобы выделить оптимальные нейроны от минимальных по одному из критериев (V̂ или Ŵ), будем соответствующие одновременно минимальные значения чисел ветвей и волокон обозначать через V̂̂ и Ŵ̂.

В заключение настоящего параграфа сделаем еще три важных замечания.

1. При выборе первого элемента x⁽¹⁾₁ и числа строк исходной матрицы мы руководствовались результатами нескольких сот синтезов формальных нейронов, могущих быть использованными для построения арифметических устройств ЭВМ; во всех этих случаях абсолютная величина x_j не превосходила нескольких единиц и по-этому исходная матрица для синтеза нейронов с V̂ строилась симметричной относительно нуля при с = 11. Это обеспечивало получение нейронов с минимальным числом волокон Ŵ (все решения проверены линейным программированием), что дало возможность решать методом автоматического перебора задачу синтеза нейронов с минимальным числом ветвей V̂, а следовательно, и задачу синтеза оптимальных нейронов.

Принципиально, однако, могут встретиться такие случаи, когда |x̂_j| > 5, что при с = 11 и симметричной относительно нуля матрице (т. е. при х⁽¹⁾₁ = -5) может привести к ошибочному результату. Чтобы полностью его исключить, можно рекомендовать следующую методику синтеза формальных нейронов с минимальным числом ветвей:

а) по заданным значениям величин d_i на ЭЦВМ решить задачу синтеза нейрона с минимальным числом волокон Ŵ при помощи метода линейного программирования; в результате получить набор x̂_j (j = 1,..., l), из которого определить х̂_j min и x̂_j max;

б) решить задачу синтеза нейрона с минимальным числом ветвей V методом автоматического перебора, задавая в качестве исходных полученные выше данные:

Вычисленную при этом одновременно с V̂ величину Ŵ (дополнительное машинное время для этого не требуется) использовать для контроля, сравнив ее со значением Ŵ, полученным при помощи метода линейного программирования.

Пример. Задана пороговая диаграмма D^θ = (0, -1, 0, 0, 2, 2, 9, 7). Необходимо построить нейрон с минимальным числом ветвей:

а) по табл. 3.1 находим d₁ = 12, d₄ = -3, d₅ = -8, d₆ = 11, d₁₀ = 0, d₁₁ = -8, d₁₂ = 8.

Используя метод линейного программирования для синтеза нейрона с минимальным числом волокон непосредственно с ленты ЭЦВМ, получаем

б) синтез нейрона с минимальным числом ветвей осуществляем при помощи метода автоматического перебора, для чего выбираем

В результате решения задачи на ЭЦВМ получаем

Минимальное число волокон W, вычисленное методами линейного программирования и автоматического перебора, совпало. Построен формальный нейрон с минимальным числом ветвей V̂ = 3 и волокон Ŵ = 12 (рис. 3.13).

Довольно большой опыт синтеза нейронов показал, что при построении надежных нейронных сетей, могущих быть использованными для нужд вычислительной техники, Не встретился ни один случай, когда оказалось бы недостаточным для получения V̂ матрицы, симметричной относительно нуля с числом строк с = 11.

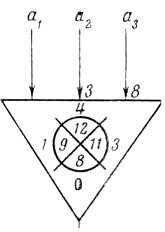
Рис. 3.13

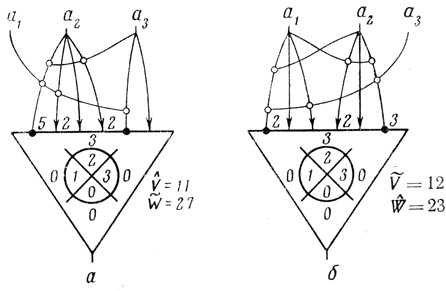
Рис. 3.14

Иначе говоря, ни в одном из важных для практики случаев не появлялась необходимость в контроле результатов путем использования методов линейного программирования.

Однако могут встретиться специально придуманные примеры (подобные приведенному выше), для которых процедура, описанная в пунктах "а" и "б", может оказаться необходимой.

Максимально необходимое машинное время для синтеза оптимальных нейронов описанным методом (при n = 3) составляет 6 мин; для контроля результатов (по Ŵ) с использованием симплексного метода требуется еще 3 мин (для ЭЦВМ М-20).

2. Синтез большого числа формальных нейронов показал, что не по всякой пороговой диаграмме может быть построен оптимальный нейрон. Например, оказалось, что по диаграмме D^θ = (0, 0, 0, 3, 0, 1, 3, 2) можно построить либо нейрон с минимальным числом ветвей V̂ = 11 и относительно наименьшим числом (из всех вариантов нейронов V̂ = 11) волокон W̃ = 27 (рис. 3.14, а), либо нейрон с минимумом волокон Ŵ = 23 и относительным минимумом ветвей Ṽ = 12 (рис. 3.14, б).

Синтез большого числа нейронов показал, что до 10% пороговых диаграмм, принятых за исходные при синтезе, не дают возможно- с и построения оптимальных нейронов.

В связи с этим весьма актуальна задача выявления критериев, которые бы по виду пороговой диаграммы D^θ = (0, γ₁,.....,γ_2ⁿ-1) позволили бы однозначно решить вопрос о возможности построения по этой диаграмме оптимального нейрона.

3. При числе входов n ≥ 4 машинное время, необходимое для синтеза оптимальных (или имеющих наименьшее число ветвей) нейронов методом автоматического перебора, становится недопустимо большим. Поэтому является актуальной задача минимизации выражения (3.83) при n > 4.