§ 3.7. Автоматический синтез оптимальных формальных нейронов

В предыдущем параграфе было показано, что по заданной пороговой диаграмме D^θ принципиально может быть синтезирован формальный нейрон, имеющий одновременно минимальное число волокон Ŵ̂ минимальное число ветвей V̂̂, т. е. - оптимальный нейрон. В связи с этим была поставлена задача полной формализации синтеза оптимальных нейронов и автоматической выдачи всей нужной для этого информации, а также и анализа полученных результатов. Задача запрограммирована для реализации на ЭЦВМ М-20 и решается в следующей последовательности (рис. 3.15).

1. По заданной диаграмме D^θ определяются параметры di, которые вводятся в программу в качестве исходной информации.

2. Методом автоматического перебора при с = 11 строках исходной матрицы параллельно вычисляются:

а) минимальное число ветвей V̂ (в результате получается один вариант, при котором W ≠ Ŵ);

б) минимальное число волокон Ŵ (в результате получается один вариант, при котором V ≠ V̂).

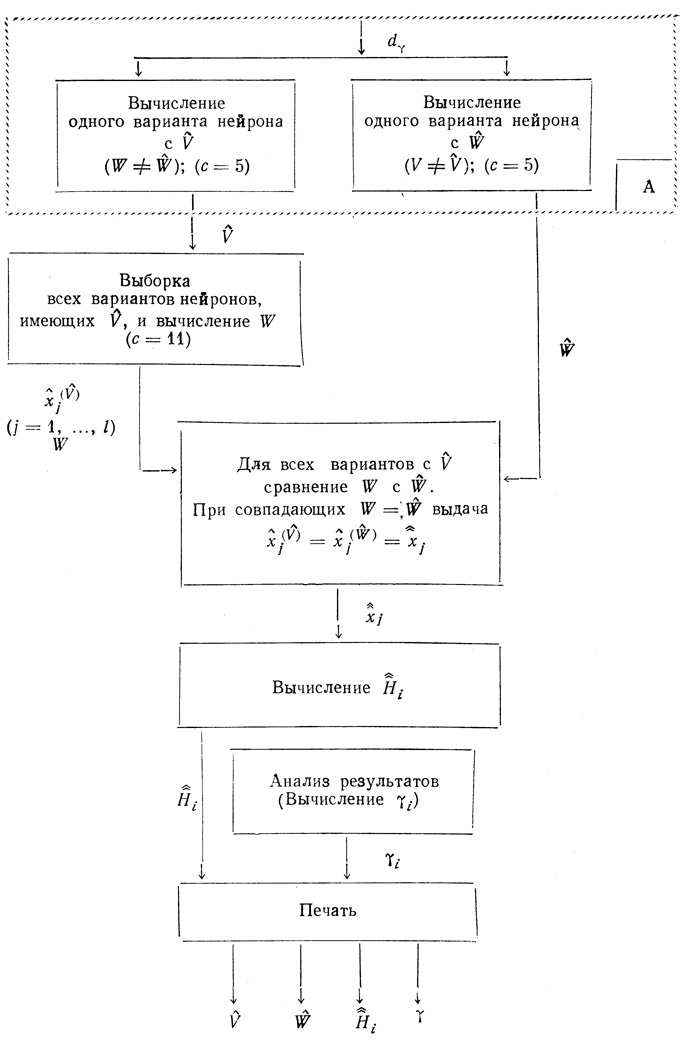
Рис. 3.15

3. Производится выборка всех вариантов нейронов (при с = 11), которые имеют минимальное (ранее вычисленное) число ветвей V̂, и для каждого из них по формуле (3.25) вычисляется значение числа волокон W (в общем случае W ≠ Ŵ).

4. Каждое из ряда значений W_k (напомним, что все соответствующие им V = V̂) сравнивается с ранее вычисленной величиной минимального числа волокон Ŵ; для всех случаев, когда W_j = Ŵ, происходит выдача наборов х̂j, которые, очевидно, обеспечивают минимальное значение как ветвей V̂̂, так и волокон Ŵ̂ обозначим х̂_j, одновременно обеспечивающее Ŵ̂ и V̂̂, через х̂̂_j.

5. Используя x̂̂_j, по формулам (3.24), (3.28) (или подобным им при n ≠ 3) вычисляются Ĥ̂_i.

6. Производится анализ полученных результатов, для чего по

каждому из наборов Ĥ̂_i вычисляется по формулам типа (3.9) соответствующий набор γ'_j; по совпадению вычисленных значений γ'_j, с исходными (заданными пороговой диаграммой D^θ) значениями γ_j можно судить о правильности решения задачи синтеза с точки зрения выполнения требуемой логической функции.

7. На печать выдаются:

а) набор значений Н̂̂_i, достаточный для однозначного построения оптимального нейрона;

б) контрольные данные: минимальные значения числа ветвей V̂̂ и волокон Ŵ̂, набор вычисленных значений γ'_j, количество перебранных вариантов z и номер варианта z_i, при котором получено данное решение.

Если рабочее число строк с = 11 позволяет получить несколько оптимальных нейронов, то на печать выдается полная информация о каждом из них в отдельности.

Образец печати показан в табл. 3.9. Приведен кусок ленты^*, дающий одно из трех оптимальных решений. Рядом с лентой показана расшифровка полученных результатов, остающаяся неизменной при синтезе любых трехвходовых нейронов. Задача решалась при тех же исходных данных, что и в примере предыдущего параграфа, т. е. для диаграммы вида: D^θ = (0, 1, -2, 1, -3, 2, 4). Для построения нейрона достаточно любого из двух наборов Н̂̂_i: либо для случая, когда имеет место V̂̂ (в табл. 3.9 обозначено как Ĥ_v), либо для случая, когда имеет место Ŵ (обозначено Ĥ̂_w); вполне очевидно, что, так как на печать выдаются только оптимальные нейроны, минимум ветвей и волокон имеет место одновременно и поэтому Ĥ_v = Ĥ_w = Ĥ̂_i. Построенный по приведенному в табл. 3.9 образцу ленты нейрон совпадает с нейроном, показанным на рис. 3.12, а.

^* (На ленте ЭЦВМ М-20 первый слева знак обозначает признак числа, второй - знак числа, третий - знак порядка, следующие две цифры - порядок числа, а последние девять цифр - мантиссу числа. Например, общее число переборов при с = 11 и z = 161051 напечатано так: ++06 161051000.)

Таблица 3.9

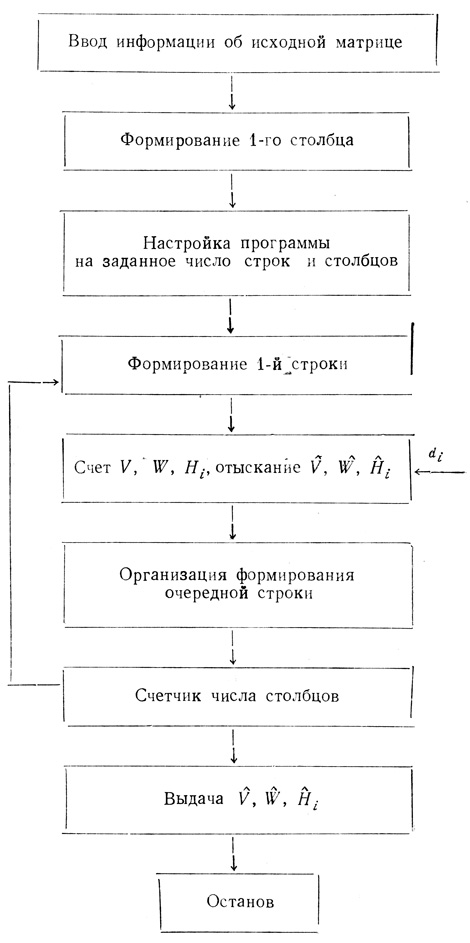
Рис. 3.16

Рассмотрим несколько подробнее блок-схему программы для решения задачи автоматического синтеза оптимальных нейронов на ЭЦВМ М-20^*.

^* (Программа разработана И. И. Грабовским.)

Часть алгоритма, выделенная на рис. 3.15 пунктиром и предназначенная для одноразового вычисления минимального числа ветвей V̂ и волокон Ŵ, реализуется программой, блок-схема которой показана на рис. 3.16. В целом блок-схема программы для реализации алгоритма автоматического синтеза оптимального формального нейрона показана на рис. 3.17. Рассмотрим работу блоков схемы.

В блоке 0 исходная информация переводится из десятичной системы в двоичную; x⁽¹⁾₁ - первый элемент первой строки исходной матрицы, с - количество строк матрицы, l - количество столбцов матрицы, d_i - параметры синтезируемого нейрона, полученные из заданной пороговой диаграммы D^θ.

В блоке 1 формируется столбец исходной матрицы по формулам:

В блоке 2 формируются константы для настройки программ блоков 4 и 5 в зависимости от заданных параметров с и l исходной матрицы.

В блоке 3 производится настройка программ блоков 4 и 5 на l циклов.

В блоке 4 формируется очередная строка, состоящая из элементов x_j исходной матрицы. В исходном состоянии (до работы блока 5) блок 4 выдает первую строку.

Блок 5 в зависимости от заданного числа столбцов l может состоять из различного числа последовательно работающих подблоков (от 5.1 до 5. l). Все подблоки, кроме подблока 5.1, формируются блоком 3 программы. В начале каждого подблока стоит счетчик с, который позволяет сделать (с - 1) переадресацию в блоке 4 и столько же раз передать управление в этот блок. При этом учитывается, что при каждой переадресации предыдущий подблок проработал один раз. Так, подблок 5.1, используя то, что блок 4 до первой переадресации выдает первую строку, после выполнения (с - 1) переадресаций в блоке 4 позволяет получить первые с строк.

После выхода из подблока 5.1 восстанавливается его счетчик с одновременно с восстановлением блока 4. В подблоке 5.2 также производится (с - 1) переадресаций и столько же обращений к блоку 4.

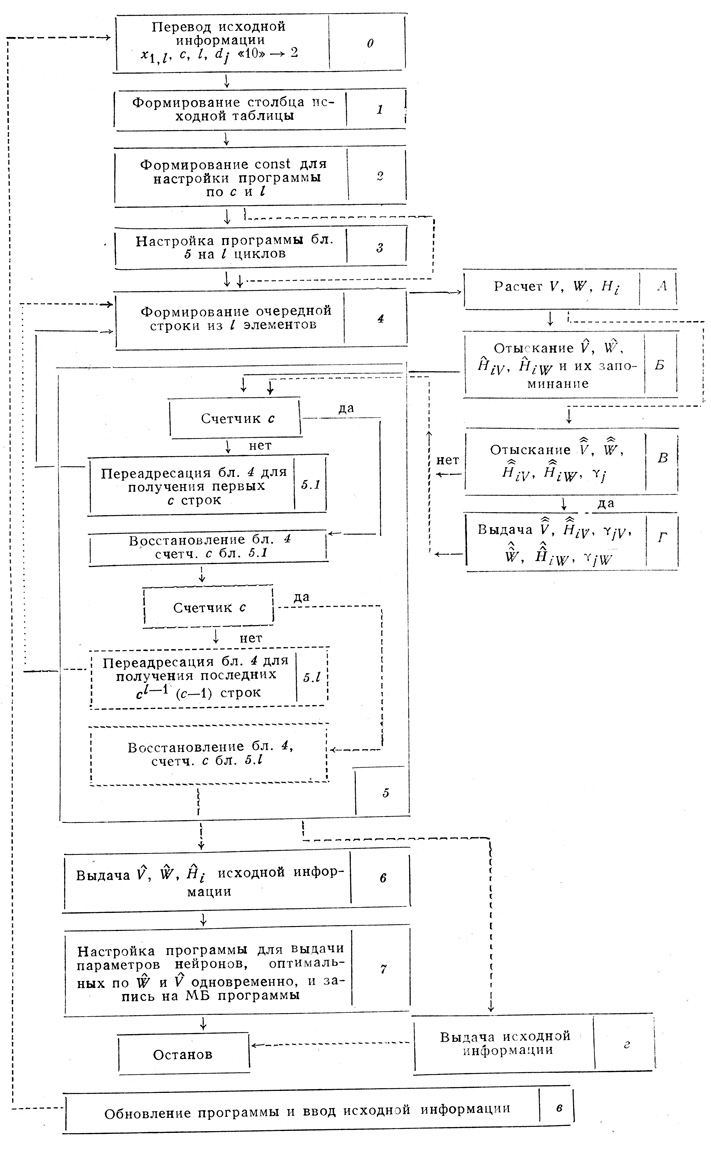
Рис. 3.17

В результате (с - 1) раз срабатывает предыдущий подблок 5.1 и дополнительно получается с (с - 1), а всего с + с (с - 1) = с² строк.

После выхода из подблока 5.2 его счетчик с восстанавливается одновременно с блоком 4.

Точно так же работает подблок 5.3, в результате чего дополнительно получаются с² (с - 1), а всего с² + с² (с - 1) = с³ строк.

В результате работы I подблоков образуются все z = с + с (с - 1) + с² (с - 1) + с³ (с - 1) + ...+ с^l-1 (с - 1) = с^l строк.

После сформирования в результате работы блоков 4 и 5 очередной строки управление передается в арифметический блок А, производящий вычисления V, W, H_i (для случая, когда n = 3). Исходной информацией для блока А являются значения х_j, соответствующие очередной строке перебора, и заданные параметры d?.

В блоке Б вычисленные значения V и W сравниваются с соответствующими величинами, вычисленными по х_j предыдущей строки. В случае если вычисленные V и W окажутся меньшими, чем вычисленные по предыдущей строке, они запоминаются взамен последних. Кроме того, запоминаются соответствующие им наборы значений Ĥ_iV и Ĥ_iW. Управление с целью формирования следующей строки передается в блок 5.

В результате работы цикла 4 - А - Б - В - 5 из всех z вычисленных значений V, W, H_iV, H_iW блоком 6 выдаются наименьшие значения V̂ и Ŵ, соответствующие им наборы Ĥ_iV и Н̂_iW, а также исходная информация.

На этом заканчивается первый цикл работы алгоритма, который на рис. 3.15 очерчен пунктиром.

В блоке 7 программа настраивается на второй цикл работы, целью которого является отыскание нейронов, одновременно имеющих минимум ветвей V̂̂ и минимум волокон Ŵ̂. В результате работы блока 7 образуются новые связи между блоками, показанные пунктиром: блок 2 - блок 4; блок А -блок В; блок В - блок 5; блок Г - блок 5; блок 5 - блок г; блок в - блок 0.

Вновь настроенная программа записывается на магнитном барабане.

После блока 7 - останов.

Нажатием кнопки "пуск" управление передается блоку в, в котором производится обновление программы и ввод с читающего устройства информации. После этого управление передается блоку 0.

В результате работы блоков В, Г и г выдается информация только об оптимальных нейронах: Н̂_iV = Ĥ_iW - Ĥ̂_i, V̂̂, Ŵ̂, γ_j и исходная информация. После этого происходит останов.

В случае, если заданная пороговая диаграмма D^θ = (0,γ₁,..., γ_2ⁿ-1) не имеет оптимального нейрона, командой с ПУ можно выдать на печать:

а) информацию о всех нейронах, имеющих минимум ветвей V̂ и соответствующие каждому из этих нейронов значения W; благодаря этому можно выбрать нейрон, имеющий минимум ветвей V̂ и относительный минимум волокон W̃;

б) информацию о всех нейронах, имеющих минимум волокон Ŵ и соответствующие каждому из этих нейронов значения V; благодаря этому можно выбрать нейрон, имеющий минимум волокон Ŵ и относительный минимум ветвей Ṽ.

Заметим, что число вариантов нейронов, имеющих минимум волокон Ŵ, примерно на порядок превосходит число вариантов нейронов, имеющих минимум ветвей V̂ (разумеется, при синтезе нейронов по одной и той же заданной диаграмме D^θ).