§ 3.8. Синтез обобщенных формальных нейронов

В § 2.2 предложено обобщение понятия формального нейрона^* с помощью построения N-слов; для описания функционирования нейронов, кроме диаграмм Венна в исчислении высказываний, порядковых, пороговых и вероятностных диаграмм, использовались также T-диаграммы и T_i-диаграммы n переменных.

^* (Такие нейроны иногда будем называть обобщенными.)

Настоящий параграф посвящен синтезу обобщенных формальных нейронов. В силу установленного соответствия между N-словами и формальными нейронами синтез последних будем начинать с построения их N-слов. В описываемом способе существенную роль будут играть запрещающие волокна (в том числе волокна типа "запрет запрета").

Допустим, что нам дана T-диаграмма n переменных D^T (a₁,... ..., а_n). Требуется построить нейрон, Т-диаграммой которого является заданная диаграмма D^T (a₁,...,а_n).

Входные слова на D^T (a₁,..., а_n) будем обозначать γ_2ⁿ-1 ,....., γ₀ (в порядке убывания номеров ячеек: 2ⁿ - 1,..., 0).

1. Слово γ_2ⁿ-1 является N-словом такого нейрона с входами a₁,.....,a_n, у которого входное слово, соответствующее элементарной последовательности 1... 1 (n единиц, в десятичной записи: 2ⁿ - 1), есть γ_2ⁿ-1;

2. Предположим, что N-слово α нейрона с n входами a₁,...,а_n у которого входные слова, соответствующие элементарным последовательностям 2ⁿ - 1,..., i (в десятичной записи), 2ⁿ - 1 ≥ i > 1, есть γ_2ⁿ-1,....,γ_i, построено, n>1.

Построим N-слово β нейрона с входами а₁,...,a_n, у которого входные слова, соответствующие элементарным последовательностям 2ⁿ - 1,..., i, i - 1, есть γ_2ⁿ-1,....,γ_i ,γ_i-1.

Пусть в (i - 1)-й элементарной последовательности переменной a_k соответствует единица, переменным a_j1,..., a_js (и только им) - нули. Образуем два М-слова: a_k(a_j1... a_js), a_j1 ... a_js.

Ко всем буквам слова α, кроме скобок (,), [,],<,>, букв, входящих во вполне круглые слова, и букв а_j1,....,а_js, ã_j1,....,ã_js припишем справа слово (а_k (а_j1 ... a_js)). Получим N-слово, которое обозначим {α}*.

Ко всем буквам слова γ_i-1, кроме скобок [,], <,> и букв а_j1,... ...,a_js)ã_j1,...,ã_js, припишем справа слово (a_j1.. a_j1). Получим N-слово, которое обозначим {γ_i-1}'.

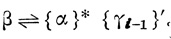
Легко видеть, что построенное N-слово является N-словом нейрона, у которого входные пороговые слова, соответствующие элементарным последовательностям 2ⁿ - 1,..., i - 1, есть γ_2ⁿ-1,...,γ_i-1.

Следовательно, по данной диаграмме D^T (а₁... а_n) можно построить N-слово μ нейрона, T-диаграммой которого является D^T (a₁,... ..., а_n):

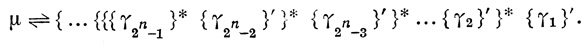
Пример 3.2. Пусть диаграмма имеет вид, показанный на рис. 3.18.

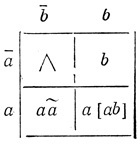
Рис. 3.18

Построим N-слово μ:

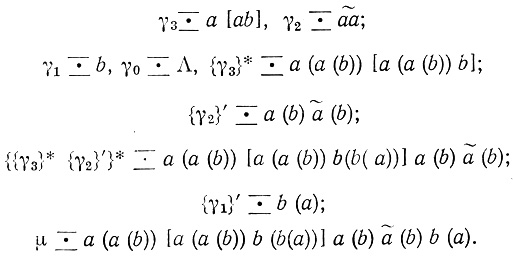
Проверка показывает, что T-диаграмма нейрона, соответствующего полученному N-олову μ (рис. 3.19), есть заданная диаграмма D^T(a, b).

Нетрудно убедиться, что построенное по заданной диаграмме D^T(n)N-слово μ, вообще говоря, не является оптимальным подлине (т. е. по числу вхождений букв алфавита ББ̃).

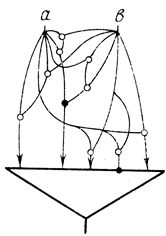
Рис. 3.19

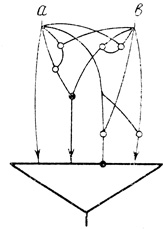
Рис. 3.20

Так, в примере 3.1 при построении {γ₃}* к первому вхождению буквы а в слове γ₃, можно не присоединять справа слово (а (b)), так как слово γ₂ начинается буквой а, тогда

μ [а (а (b)) b (b (a))] a (b) b (а);

соответствующий нейрон приведен на рис. 3.20.

Если нам известна не Т-диаграмма, а пороговая диаграмма n переменных D^θ (а₁,..., а_n), то синтез нейрона можно начинать с построения Т-диаграммы, соответствующей D^θ (а₁,..., а_n). Из определения веса входных слов (§ 2.2) следует, что Т-диаграмма, соответствующая заданной D^θ (a₁,..., а_n), находится неоднозначно.

Пример 3.3. Дана диаграмма D^θ (a, b) (0, 1, 0, 3). Необходимо построить нейрон, пороговой диаграммой которого будет (а, b).

Найдем Т-диаграмму D^T (а, b): последовательности 00 соответствует пустое слово (см. определение Т-диаграммы n переменных (§ 2.2)), последовательности 01 поставим в соответствие входное слово b, _[b_] = 1, последовательности 10- аа̃, _[aã_] = 0, последовательности 11 - a [ab], _[a [аb]_] = 3. Выбранная Т-диаграмма совпадает с диаграммой на рис. 3.18, синтез нейрона по которой приведен в примере 3.2.

О реализации формул исчисления высказываний на формальных нейронах. Пусть Φ - формула исчисления высказываний, составленная из переменных a₁,....,a_n.

Говорят, что формула Φ реализуется на формальном нейроне А с входами a₁,..., а_n (входы обозначены теми же буквами, что и переменные, из которых составлена формула Φ), если имеется такое значение порога нейрона А, при котором А возбуждается тогда и только тогда, когда формула Φ принимает значение 1 (1 - истина, 0 - ложь; у нейронов: 1 - возбужденность, 0 - не возбужденность).

Покажем, что для любой формулы Φ исчисления высказываний можно построить нейрон (и не один), на котором она реализуется.

Действительно, пусть D^ρ̄ (a₁,....,а_n) - вероятностная диаграмма, соответствующая формуле Φ (способы построения D^ρ̄ (a₁,..., а_n) описаны в главе 1: от формулы Φ переходим к диаграмме Венна, от диаграммы Венна к вероятностной диаграмме, черта над буквой р означает, что на диаграмме нет букв р). Построим пороговую диаграмму (a₁,..., а_n).

Возьмем 2ⁿ произвольных целых чисел δ₁,..., δ_2ⁿ, среди которых есть по крайней мере один нуль, поставим их в соответствие элементарным последовательностям переменных a₁,...,а_n (каждой последовательности - только одно число), обозначая буквами γ₀,... ...,γ_2ⁿ-1 (индексы букву - числа, двоичная форма записи которых совпадает с соответствующими элементарными последовательностями) так, что последовательности номер 0 соответствует нуль (γ₀ = 0) и γ_min > γ_max (γ_βs+1,....,γ_β2ⁿ), где β₁,...,β_s -номера ячеек на D^ρ̄ (a₁,...,a_n),содержащих единицы; γ_min↔min(γ_β1,...,γ_βs)- если на D^ρ̄(a₁,...,a_n) есть единицы; γ_max↔max(γ₀,...,γ_2ⁿ-1) + 1 если на D^ρ̄ нет единиц (в этом и только в этом случае Φ ≡ 0).

По диаграмме D^θ (a₁,..., а_n) начертим нейрон A (a₁,....,а_n). На нейроне А (a₁,..., а_n) можно реализовать формулу Φ. Выберем интервал изменения его порога {θ₁,..., θ_r} так, что γ_min ∈ {θ₁,..., θ_r}. Если порог нейрона А равен γ_min, то нейрон А возбуждается тогда и только тогда, когда формула Φ принимает значение 1.

Пример 3.4. Пусть Φ (ab ∨ а̄b) - формула, составленная из переменных а, b. Она принимает значение 1 только тогда, когда переменные образуют одну из элементарных последовательностей: 01, 11.

Составим пороговую диаграмму D^θ (а, b) ↔ (0, 1, 0, 3), γ_min = 1. Выбранная диаграмма совпадает с(а, b), заданной в примере 3.3. Таким образом, формула (ab ∨ āb) реализуется на каждом из нейронов на рис. 3.19 и 3.20.